Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[84] nadorp

2004-03-10 10:00:50

OKTV III/2. megoldásvázlat:

Ha k=2^rk₀,ahol k₀ páratlan, akkor 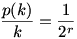$\frac{p(k)}k=\frac1{2^r}$ , ezért

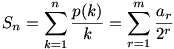$S_n=\sum_{k=1}^{n}\frac{p(k)}k=\sum_{r=1}^{m}\frac{a_r}{2^r}$ , ahol m=[log₂n]

Itt a_r értéke annyi, ahány olyan szám van 1-től n-ig, amelynek a 2^r pontos osztója. Így könnyen látható, hogy $a_r=\left[\frac{n}{2^r}\right]-\left[\frac{n}{2^{r+1}}\right]$ , ezért

$S_n=\sum_{r=0}^{m}\left({\left[\frac{n}{2^r}\right]-\left[\frac{n}{2^{r+1}}\right]}\right)\frac{1}{2^r}=n+\left[\frac{n}{2}\right]\left(\frac12-1\right)+\left[\frac{n}{4}\right]\left(\frac14-\frac12\right)+ ...+ \left[\frac{n}{2^m}\right]\left(\frac1{2^m}-\frac1{2^{m-1}}\right)=n-\sum_{r=1}^{m}\left[\frac{n}{2^r}\right]\frac1{2^r}$

Az alsó becsléshez elég felhasználni, hogy $\left[\frac{n}{2^r}\right]\le\frac{n}{2^r}$ és a mértani sorozat összegképletét

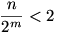
A felső becsléshez felhasználjuk, hogy $\left[\frac{n}{2^r}\right]\ge\frac{n}{2^r}-\frac{2^r-1}{2^r}$ , megint a mértani sorozat összegképletét és végül, hogy $\frac{n}{2^m}<2$

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[83] Adus

2004-03-09 22:31:07

Sziasztok! Nagyon megköszönném, ha az OKTV III. kategória 2. és 3. feladatának megoldását közreadnátok.

Köszönöm!!!

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[82] Kós Géza	2004-03-05 14:54:06
Szerintem jó a megoldásod.
Előzmény: [81] lorantfy, 2004-03-05 13:58:59

[81] lorantfy	2004-03-05 13:58:59
Sziasztok! Én a III./1. példát elég könnyűnek találom, ha valami gond van az alábbi gondolatmenettel szóljatok: OKTV III./1. megoldásvázlat: Legyen az ABC $\Delta$ legkisebb szöge $\alpha$ $\geq$ 60^o Növeljük az AB és AC oldalakat $\sqrt{2}$ hosszúra (ha rövidebbek). Az ABC $\Delta$ nyilván benne van az így keletkező AEF $\Delta$ -ben. Vegyük fel a kocka egyik oldallapjának oldalain a G csúcsból a $\frac{EF}{\sqrt{2}}$ szakaszokat. Ekkor EF átfogójú derékszögű háromszöget kapunk. $\sqrt{2} \leq EK=FK$ , mivel FK az FKH derékszögű $\Delta$ átfogója, melynek KH befogója $\sqrt{2}$ . EFA és EFK azonos alapú egyenlő szárú $\Delta$ -k. FA $\leq$ FK, így az A pont az EFK $\Delta$ belsejébe esik (vagy megegyezik K-val), amit tartalmaz az egységélű kocka.

Előzmény: [75] Csillag, 2004-03-04 17:39:09

[80] BrickTop	2004-03-04 22:32:36
A 2. feladatot szerintem mindenki meg tudta csinálni. Az 1.-vel lehetett a legtöbb időt elvesztegetni, sokféleképpen neki lehet menni egy ilyen feladatnak. Én nem sokra jutottam, kifejeztem a CY szakasz hosszát ismert adatokból, ezek alapján elvileg megszerkeszthető, dehát ez nem a legideálisabb megoldás :( A 3. feladatot nem(/sem) tudtam megcsinálni, de ezt sajnálom a legkevésbé, mert nem hiszem, hogy eszembe jutott volna ez az ötlet. Ülhetnék rajta egy hétig, akkor se ugrana be. A 3.-ra sok időt se lehetett pazarolni, rögtön látszott rajta hogy vagy beugrik, vagy nem.
Előzmény: [77] tassyg, 2004-03-04 18:35:45

[79] tassyg

2004-03-04 22:31:13

Kedves Endre!

A 2. feladatnál úgy tűnik, Te is figyelmen kívül hagytad, hogy az oldalhosszak különböző egész számok, így a (2;2;3) nem jó megoldás. Nekem elég sok eset vizsgálata után a (6;7;12), valamint a (7;8;9) jöttek ki, melyekre a szorzat egyaránt 504. Becslésekkel és néhány eset kipróbálásával ki lehetett zárni a leghosszabb oldal 12-nél nagyobb értékeit. De azért kíváncsi vagyok, volt-e rá valami "szép" megoldás.

Előzmény: [78] Csóka Endre, 2004-03-04 22:19:46

[78] Csóka Endre

2004-03-04 22:19:46

Sziasztok!

Egy-egy nagyon tömör megoldásvázlat a II. kategóriás feladatokhoz (én túlkoros voltam ehhez, de azért megoldottam):

1. P helyének nyilván lineáris függvénye X és Y pont helye, így az XY vektor is. Ez a két szélső helyzetben az AC, illetve a CB vektor. Ha tehát az XY vektort az A kezdőpontba toljuk, akkor a végpont helye C és D között lineárisan változik, ahol D az a pont, melyre (CB vektor)=(AD vektor). Ekkor nyilván akkor a legrövidebb a szakasz, amikor merőleges CD-re, ami egybeesik a súlyvonallal. Mivel ez az eredeti vektor eltoltja, így a merőlegesség arra is igaz. Az XY vektor ismeretében P szerkesztése pedig triviális.

2. Legyen a harmadolópont az ABC háromszög AB oldalának A-hoz közelebbi harmadolópontja. A területfelezésből következik, hogy az egyenes BC-t 3:1 arányban osztja (2/3 * 3/4 = 1/2). Tehát a kerületfelezésből AB/3+BC/2=CA. Könnyű meggondolni, hogy ez csak úgy lehet, ha 3|AB, 2|BC, és így 2<=CA. AB=3, BC=CA=2 ezért a legkisebb megfelelő.

3. Az 1, 2, 4, 8(, 16) elemek be-, vagy nem beválasztásának megválasztásával a 16, ill. 32 különböző maradék mindegyike előáll, ezzel a részhalmazokat maradék szerint egyenlő csoportokba oszthatjuk. Tehát mindkét oldalon az összes részhalmaz számának 1/16-a áll.

Előzmény: [77] tassyg, 2004-03-04 18:35:45

[77] tassyg

2004-03-04 18:35:45

Sziasztok!

A matematika OKTV II. kategóriás döntőjének feladatai:

1. A P pont a hegyesszögű ABC háromszög AB oldalán mozog. A P-n át AC-vel húzott párhuzamos a BC oldalt az X pontban, a P-n át BC-vel húzott párhuzamos pedig AC-t az Y pontban metszi. Adjunk eljárást olyan P pont szerkesztésére, amelyhez tartozó XY szakasz a lehető legrövidebb. Bizonyítsuk be, hogy a legrövidebb XY szakasz merőleges a C csúcsból induló súlyvonalra.

2. Egy háromszög oldalhosszai különböző egész számok; a háromszöghöz található olyan egyenes, amely átmegy a legnagyobb oldal valamelyik harmadoló pontján, és felezi a háromszög területét és kerületét is. Határozzuk meg az oldalhosszakat úgy, hogy azok szorzata a lehető legkisebb legyen.

3. Legyen H a 2004-nél nem nagyobb pozitív egészek halmaza: H={1;2;3;...;2004}. Jelölje D a H halmaz olyan részhalmazainak számát, amelyekben az elemek összegét 32-vel osztva 7-et kapunk maradékul, és jelölje S a H halmaz olyan részhalmazainak számát, amelyekben az elemek összegét 16-tal osztva 14-et kapunk maradékul. Igazoljuk, hogy S=2D.

Amúgy kinek milyen lett?

Előzmény: [76] Csizmadia Gábor, 2004-03-04 17:47:24

[76] Csizmadia Gábor

2004-03-04 17:47:24

Sziasztok! A II. kat.-os feladatokat be tudnátok írni?

Köszi: Cs. G.

[75] Csillag

2004-03-04 17:39:09

Sziasztok!

Az OKTV III. kategória döntő feladatai azoknak, akik még nem ismerik:

1. Egy háromszög mindhárom oldala legfeljebb 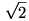$\root\of 2$ hosszúságú. Bizonyítsuk be, hogy belefoglalható egy egységnyi élű kockába.

2. Jelölje p(k) a k természetes szám legnagyobb páratlan osztóját. Bizonyítsuk be, hogy minden n $\ge$ 1-re

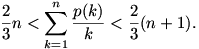
$\frac23n<\sum_{k=1}^n\frac{p(k)}k<\frac23 (n+1).$

3. Bizonyítsuk be, hogy a c és d egész számokhoz akkor és csak akkor létezik végtelen sok különböző x_n,y_n(n=1,2,...) egész számpár, amelyre x_n osztója cy_n+d-nek és y_n osztója cx_n+d-nek, ha c osztója d-nek. (c,d,x_n és y_n nem feltétlenül pozitív számok.)

Akik részt vettek: hogy sikerült?

[74] macilacibubu	2004-03-02 22:10:47
Sok sikert mindenkinek a csütörtöki OKTV-hez.

[73] BrickTop	2004-02-25 16:36:12
Jó, hogy a saját kérdésemre válaszolok, de én ma kaptam meg a hivatalos papírt :)
Előzmény: [72] BrickTop, 2004-02-24 15:08:04

[72] BrickTop	2004-02-24 15:08:04
II. kategória: Nemhivatalos forrásból mi is értesültünk a továbbjutásokról, de még mindig nem küldték ki a "behívókat". Nektek már igen?

[71] Zitusbutus	2004-02-17 16:51:59
Sziasztok gratulálok mindenkinek, aki továbbjutott nekem sajnos nem sikerült (2 ponton múlott állítólag) sikeres versenyzést

[70] Csizmadia Gábor

2004-02-16 18:26:38

És az egyik maxpontos monogrammja GB.;-)

Üdv: Cs.G.

Előzmény: [68] tassyg, 2004-02-15 22:17:36

[69] tassyg

2004-02-15 22:30:35

Bocsánat, a "megbízható forrásom" úgy tudta, hogy 5 feladat van, azért számolt 35 pontot. Mivel valójában csak 4 volt, így már minden érthető a 28 ponttal... :-)))

Előzmény: [68] tassyg, 2004-02-15 22:17:36

[68] tassyg

2004-02-15 22:17:36

Kedves Fórumosok!

Meg nem erősített, de megbízható forrásból úgy tudom, hogy a Mat. II. kategóriás OKTV döntőjének ponthatára 24 pont. Azt hiszem, 54 személyt hívtak be. És állítólag a legjobb is csak 28 pontos lett a 35-ből... :-))

Üdvözlettel: Tassy Gergely

[67] iron	2004-02-11 21:10:14
Kedves Géza, Lorantfy, köszönöm a tanácsokat, így már tényleg nem egy nehéz példa :) Nem jó dolgok helyett vezettem be új ismeretleneket, és elég ronda egyenlőtlenség jött ki, nem tudtunk vele mit kezdeni.
Előzmény: [65] lorantfy, 2004-02-10 22:18:51

[66] LPilot	2004-02-11 19:43:44
Üdv mindenkinek.Az a kérdésem, hogy a matek OKTV döntőbe jutáshoz megvannak-e már a ponthatárok, ha igen mennyi az, ha nem, akkor meg mikorra várhatóak? Ha eddig nem kaptam meg a behívómat (mármint a döntőbe, mert a Honvédség már invitált :) ), akkor ne is reménykedjek? Köszi

[65] lorantfy

2004-02-10 22:18:51

Kedves Iron!

Géza ötletei tökéletesen beválnak: tizes alapra, aztán a kéttagú szorzatok logaritmusára új változókat, aztán számtani-mértani közép és kész is. De gondolom azóta Te is kipróbáltad. Hiába erölködök nem tudok mást kitalálni!

Előzmény: [63] iron, 2004-02-09 18:11:59

[64] Kós Géza

2004-02-09 20:15:48

Az ilyen feladatoknál a legfontosabb rutin lépés, hogy átírod egyforma, lehetőleg állandó alapú logaritmusra. Mondjuk 10-esre.

Egy másik dolog, ami ebben a feladatban nagyon jól látszik, hogy az xy, yz, zx kifejezéseket (vagy ezek logaritmusát) érdemes valamilyen más betűvel megjelölni, ugyanis x²yz=xy^.zx, xy²z=xy^.yz és xyz²=yz^.zx.

Előzmény: [63] iron, 2004-02-09 18:11:59

[63] iron	2004-02-09 18:11:59
Szia Lorantfy! Kösz, hogy megnézed a példát, ez a következő: 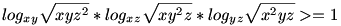$log_{xy}\sqrt{xyz^2}log_{xz}\sqrt{xy^2z}log_{yz}\sqrt{x^2yz}>=1$ Tudjuk, hogy x,y,z>0, de egyik sem 1. Még megpróbálom új ismeretlenek bevezetése + másodfokú kifejezés alulról becslésével, egy ismerősömnek állítólag úgy kijött. Üdv: Iron
Előzmény: [62] lorantfy, 2004-02-05 20:19:37

[62] lorantfy

2004-02-05 20:19:37

Hello Iron!

Légyszives írd be a 2. ford. I.kat/utolsó feladatát, mert nem találom a neten. (Nem kell szépen) Kösz! L.

Előzmény: [59] iron, 2004-02-05 16:48:50

[61] SchZol

2004-02-05 19:45:39

A II. kategóriájé még nincs meg, szerintem leghamarab jövőhét közepén, legkésőbb egy hétre rá. A III. kategóriájé azért van meg, mert az még decemberben volt és abból nincs második forduló, hanem rögtön a döntő!

Üdv, Zoli

Előzmény: [60] landuk, 2004-02-05 18:38:57

[60] landuk

2004-02-05 18:38:57

Hello!

A II. kategória ponthatárai is megvannak? Ha valaki tudja, írja ide! Pont ma nem mentem suliba, amikor megjön az eredmény! :(

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?