Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[746] gajdocsi11

2014-11-28 20:53:06

Szerintem el lehet érni, hogy mindkettőt elfogadják. :)

Én egyébként az idei sort valamivel könnyebbnek találtam, mint a tavalyit, de ha ebben nincs is igazam, szerintem sokkal élvezetesebb feladatok voltak kiírva. 5 óra alatt azért meg tud élni az ember mélypontokat, de idén lkötött végig.

Piros pont a szervezőknek! :D

Előzmény: [744] Kovács 972 Márton, 2014-11-28 19:34:21

[745] Kovács 972 Márton

2014-11-28 20:30:21

Egyébként a feladatok az alábbiak voltak:

1. Tekintsük azokat az ötjegyű számokat, amelyek az 5,6,7,8 számjegyeket tartalmazzák és mindegyiket legalább egyszer. Mennyi ezeknek az ötjegyű számoknak az összege?

2. Legyen &tex;\displaystyle C&xet; az &tex;\displaystyle AB&xet; szakasz belső pontja. Az &tex;\displaystyle AB&xet; szakasz azonos oldalára emeljük az &tex;\displaystyle AB, AC&xet; és &tex;\displaystyle CB&xet; átmérőjű köröket. A &tex;\displaystyle C&xet; ponton át az &tex;\displaystyle AB&xet;-re emelt merőleges egyenes az &tex;\displaystyle AB&xet;-re emelt félkörívet a &tex;\displaystyle D&xet; pontban metszi. Az &tex;\displaystyle AD&xet; szakasz és az &tex;\displaystyle AC&xet;-re emelt félkörív metszéspontja &tex;\displaystyle E&xet;, a &tex;\displaystyle BD&xet; szakasz és a &tex;\displaystyle CB&xet;-re emelt félkörív metszéspontja &tex;\displaystyle F&xet;. Igazoljuk, hogy az &tex;\displaystyle EF&xet; egyenes az &tex;\displaystyle AC&xet;-re illetve &tex;\displaystyle CB&xet;-re emelt félkörívek közös érintője lesz.

3. Legyen &tex;\displaystyle a_1=1&xet;, a sorozat további elemeit pedig a következő összefüggés határozza meg:

&tex;\displaystyle a_{n+1}a_n=4(a_{n+1}-1)&xet; &tex;\displaystyle n&xet; pozitív egész.

Igazoljuk, hogy a sorozat első 2025 darab tagjának a szorzata nagyobb, mint &tex;\displaystyle 2^{2014}&xet;.

4. Az &tex;\displaystyle ABC&xet; háromszög kerülete 12 &tex;\displaystyle cm&xet;, területe 6 &tex;\displaystyle cm^2&xet;. Legyen &tex;\displaystyle P&xet; az &tex;\displaystyle ABC&xet; háromszög egy belső pontja. A &tex;\displaystyle P&xet; pontnak a &tex;\displaystyle BC, CA&xet; és &tex;\displaystyle AB&xet; oldalak egyeneseire vonatkozó merőleges vetületei legyenek rendre &tex;\displaystyle D, E&xet; és &tex;\displaystyle F&xet;. Tekintsük az alábbi összeget:

&tex;\displaystyle S=\frac{BC}{PD}+\frac{CA}{PE}+\frac{AB}{PF}&xet;

&tex;\displaystyle (a)&xet; Határozzuk meg &tex;\displaystyle S&xet; minimális értélét.

&tex;\displaystyle (b)&xet; A háromszög mely &tex;\displaystyle P&xet; belső pontjára lesz &tex;\displaystyle S&xet; értéke minimális?

5. Oldjuk meg a valós számok halmazán az alábbi egyenletrendszert:

&tex;\displaystyle sin^2x+cos^2y=y^2&xet;

&tex;\displaystyle sin^2y+cos^2x=x^2&xet;

Megköszönném, ha valaki feltenné a spec. matekos OKTV első fordulójának feladatsorát. (az ideit)

[744] Kovács 972 Márton

2014-11-28 19:34:21

Én a korábbi hozzászólásomban az első értelmezés szerint.

Szerintem ha többen is jelzik ezt a félreértést, akkor az lenne a "fair" hogyha mindkét megoldásra járna a maximum pontszám (természetesen amennyiben helyes). Vagyis készíteni kellene egy másik megoldókulcsot.

De pont emiatt kérdeztem, hogy mit lehet ilyenkor csinálni. Az én véleményem az, hogy az idei példák nehezebbek voltak, mint a tavalyiak, tehát szerintem a ponthatár lejjebb csúszik valamivel.

Előzmény: [743] gajdocsi11, 2014-11-28 17:21:00

[743] gajdocsi11

2014-11-28 17:21:00

Szerintem azért elég sok múlhat rajta! Vegyük azt, hogy tavaly a továbbjutás ponthatára 35/24 pont volt. Tehát ha valaki félreértelmezte és netalántán csak az egyiket fogadják el, akkor a peches csoportnak majd' 30 pontot kéne írnia a továbbjutáshoz. Én például ha 7 pontot számolok magamnak erre a feladatra, akkor 27 pontom lesz, ha nem fogadják el, akkor jó, ha részpontokat kapok, ami már nagyon necces.

Te melyik alapján csináltad meg?

Előzmény: [742] Kovács 972 Márton, 2014-11-28 17:12:46

[742] Kovács 972 Márton

2014-11-28 17:12:46

Ebben igazad van, de ezt írhatták volna akkor úgy is (ami szerintem sokkal logikusabb és semmi esetre sem érthető félre) hogy:

Tekintsük azokat az ötjegyű számokat, amelyeknek valamely 4 jegye az 5,6,7,8 számokból kerül ki (mindegyiket fel kell használni) az ötödik jegye pedig tetszőleges.

Eddig a megkérdezettek közül 8-can mondták, hogy a második értelmezés a helytálló, és 7-en, hogy az első. Ez pedig elegendően sok már ahhoz, hogy kijelenthessük, a feladat szövege nem egyértelmű.

Nem hiszem, hogy fog ezen múlni bármi is, de ha esetleg mégis, mit lehet ilyenkor tenni?

Előzmény: [740] HoA, 2014-11-28 16:20:47

[741] gajdocsi11

2014-11-28 17:12:16

Szia!

De jó, hogy itt is felvetődött a probléma. Ma igen összevesztem a matektanárommal ezen. :)

Nálunk is a társaság egyik fele így, a másik úgy oldotta meg. Nekem eszembe sem jutott volna egy olvasás után másféle számjegyeket belepakolni, így csak az 5, 6, 7, 8 számjegyekkel oldottam meg.

Félek tőle, hogy a megoldókulcs ellenem lesz, de szinte biztos vagyok benne, hogy nem így lesz.

Ez az 1. kör 1. fordulója volt, visszanézve a korábbi évek feladataira, irreálisan nehéz lenne azokhoz képest, ha bármilyen számjegy használható lenne. Többször végig kellett számolnom, mire kijött.

Ha kell, írok a szervezőknek is, mert nem tartanám fair-nek, ha nem fogadnák el az én verziómat.

Ahogy már előttem leírták, a "tartalmaz" szó pozíciója a szövegben lehetővé teszi a félreértést, mert többféleképpen lehet hangsúlyozni a mondatrészt (legyen magyar óra, a magyar nyelv szabályai szerint IS). Ha bármilyen számjegyet tartalmazhatna a szám, a harmadik mondatrész felesleges volna.

Meglepődnék, ha a megoldókulcs nem így gondolná. :)

Egyébként nektek hogy sikerült? Hány pontra számítotok? :)

Előzmény: [737] Kovács 972 Márton, 2014-11-27 21:55:16

[740] HoA

2014-11-28 16:20:47

Attól félek, a második. Nézzünk egy példát. Vitatja-e valaki, hogy az 15678 egy ötjegyű szám, amelyik tartalmazza az 5,6,7,8 számjegyeket? És persze mindegyiket legalább egyszer, de ez szerintem is elhagyható.

OFF A többi inkább nyelvészet. A félreértést szerintem a szórend okozta. Ha azt mondom: "amelyek az 5,6,7,8 számjegyeket tartalmazzák" , annak kicsit olyan hangulata van, mintha ott állna mögötte "és csak ezeket" - de nem áll ott. Ha azt mondom: "amelyek tartalmazzák az 5,6,7,8 számjegyeket" , akkor úgy érzem, arról nem szólok, mást tartalmaznak-e, tehát 15678 nyilván megfelel. OFF

Előzmény: [737] Kovács 972 Márton, 2014-11-27 21:55:16

[739] w	2014-11-27 23:16:56
Indirekt: ha a második lenne igaz, akkor felesleges lenne a "mindegyiket legalább egyszer".
Előzmény: [737] Kovács 972 Márton, 2014-11-27 21:55:16

[738] jonas	2014-11-27 22:48:35
Én az elsőre tippelnék.
Előzmény: [737] Kovács 972 Márton, 2014-11-27 21:55:16

[737] Kovács 972 Márton

2014-11-27 21:55:16

Sziasztok!

Szerintetek hogyan kell érteni az alábbi feladatot? Ma volt a 2. kategóriás OKTV, ez volt az első feladat. Én csípőből oldottam meg, nem is gondolkoztam, hogy másképp lehet-e értelmezni, aztán a végén ábrándítottak ki, hogy márpedig igen. Én kitartok a saját igazam mellett. Ti mit gondoltok?

A feladat szövege szóról szóra:

"Tekintsük azokat az ötjegyű számokat, amelyek az 5,6,7,8 számjegyeket tartalmazzák és mindegyiket legalább egyszer. Mennyi ezeknek az ötjegyű számoknak az összege?"

Az én értelmezésem:

A szám jegyei az 5,6,7 és 8 számjegyekből kerülnek ki úgy, hogy mindegyik legalább 1-szer szerepel. (tehát vagy 2 darab 5, vagy 2 darab 6, vagy 2 darab 7, vagy 2 darab 8-cas van)

A többiek szerint:

Valamelyik 4 jegye az 5,6,7 és 8 valamilyen sorrendben, az 5. pedig bármi.

[736] Róbert Gida

2014-03-26 15:22:24

"c'=16 esetén a következő út jó: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8. Így ezt az utat felszorozva c/16-tal megkaptuk a fenti tulajdonságú javító utat"

Van rövidebb javító út is! Géppel meg is lehet találni a legrövidebbet, mindössze egy párt kell felbontanunk: c'=11236-ra egy javító út: 11236,213,11023,5618, ezt &tex;\displaystyle \frac {c}{11236}&xet;-tal felszorozva kapjuk az utat, azaz:

&tex;\displaystyle c,\frac{213c}{11236},\frac{11023c}{11236},\frac c2&xet;.

(Természetesen c egy osztója volt a 11236).

Előzmény: [734] Janyolka, 2014-03-26 07:27:26

[735] Fálesz Mihály

2014-03-26 11:03:04

Ugyanennek az ötletnek egy másik megvalósítása a következő.

Veszünk olyan &tex;\displaystyle a&xet; és &tex;\displaystyle b&xet; páratlan pozitív egészeket, amikre &tex;\displaystyle a^2<c&xet; és &tex;\displaystyle a^2+c=b^2&xet;. Ezután egy párosítás a következő lesz:

&tex;\displaystyle (1,a^2-1)&xet;, &tex;\displaystyle (2,a^2-2)&xet;, ..., &tex;\displaystyle \bigg(\frac{a^2-1}2,\frac{a^2+1}2\bigg)&xet;; ezekben a két tag összege mindig &tex;\displaystyle a^2&xet;,

továbbá &tex;\displaystyle (a^2,c)&xet;, &tex;\displaystyle (a^2+1,c-1)&xet;, ..., &tex;\displaystyle \bigg(\frac{c+a^2-1}2,\frac{c+a^2+1}2\bigg)&xet;, ezekben az összeg mindig &tex;\displaystyle a^2+c=b^2&xet;.

Már "csak" a megfelelő &tex;\displaystyle a&xet; és &tex;\displaystyle b&xet; hiányzik.

Ilyeneket úgy kaphatunk, hogy az &tex;\displaystyle c&xet;-t olyan &tex;\displaystyle b-a&xet; és &tex;\displaystyle b+a&xet; tényezők szorzatára bontjuk, amelyek "közel" vannak egymáshoz, és a legnagyobb közös osztójuk &tex;\displaystyle 2&xet;. Mivel &tex;\displaystyle c=(2\cdot19\cdot53)^{2014}&xet;, a &tex;\displaystyle 19&xet; és a &tex;\displaystyle 53&xet; tényezőket kell elosztanunk a &tex;\displaystyle b+a&xet; és a &tex;\displaystyle b-a&xet; között.

Például a &tex;\displaystyle b+a=2\cdot 19^{327}\cdot 53^{1687}&xet;, &tex;\displaystyle b-a=2^{2013}\cdot 19^{1687}\cdot 53^{327}&xet; választással

&tex;\displaystyle \frac{b+a}{b-a} = 2^{-2012}\cdot\bigg(\frac{53}{19}\bigg)^{1360}\approx1,73<2, &xet;

így &tex;\displaystyle b+a<\sqrt{2c}&xet; és &tex;\displaystyle b-a>\sqrt{c/2}&xet;, tehát

&tex;\displaystyle a<\frac{\sqrt{2c}-\sqrt{c/2}}2<\sqrt{c}.&xet;

Előzmény: [734] Janyolka, 2014-03-26 07:27:26

[734] Janyolka

2014-03-26 07:27:26

3. feladat

Legyen &tex;\displaystyle 2014^{2014}=c&xet;. Megmutatatjuk, hogy van 1, 2, ..., c számoknak olyan teljes párosítása, hogy minden párban az összeg négyzetszám. Ebből már következik, hogy Boglárkának van nyerő stratégiája.

Induljunk ki a (t, c-t) párosításból. Ebben a párosításban minden összeg négyzetszám és 1-től c-ig csak c/2-nek és c-nek nincs párja. Most mutatunk egy javító utat c-ből c/2-be, úgy hogy az út minden élén a végpontok összege négyzetszám, és minden második élén az összeg c. Ekkor az út párosadik éleit kidobva (t, c-t) párosításból és a páratalanadik éleket hozzávéve, egy teljes párosítást kapunk 1, 2, ..., c számokon.

c'=16 esetén a következő út jó: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8. Így ezt az utat felszorozva c/16-tal megkaptuk a fenti tulajdonságú javító utat.

[733] w	2014-03-07 16:32:12
/2. feladat = A.267/
Előzmény: [732] Erben Péter, 2014-03-07 07:43:21

[732] Erben Péter

2014-03-07 07:43:21

A III. kategória döntőjének feladatai. (Ne lőjük le rögtön a megoldásokat.)

1. Adott az ABC háromszög. Bocsássunk merőlegest A-ból a B-beli belső szögfelező egyenesre, és B-ből az A-beli belső szögfelező egyenesre. A talppontokat jelölje D, illetve E. Bizonyítsuk be, hogy a DE egyenes a háromszög AC és BC oldalát a beírt kör érintési pontjában metszi.

2. A p és q pozitív számokra p+q $\le$ 1. Igazoljuk, hogy bármely m,n pozitív egészekre (1-p^m)ⁿ+(1-qⁿ)^m $\ge$ 1.

3. Az 1,2,...,2014²⁰¹⁴ számok közül Aladár és Boglárka felváltva törölnek le egy számot (Aladár kezd), amíg csak két szám marad. Ha a megmaradó két szám összege négyzetszám, akkor Boglárka nyer, egyébként Aladár. Kinek van nyerő stratégiája?

[731] Fálesz Mihály

2013-12-19 21:13:08

Legyen &tex;\displaystyle K&xet; olyan valós szám, ami "elválasztja" az &tex;\displaystyle a_i&xet;-ket a &tex;\displaystyle b_i&xet;-ktől, azaz &tex;\displaystyle a_1,\dots,a_n \le K \le b_1,\dots,b_n&xet;. (Választhatjuk &tex;\displaystyle K=a_n&xet;-et is.) A megoldást egyszerűbb úgy leírni, hogy bevezetjük az &tex;\displaystyle x_1\ge\dots\ge x_n\ge0&xet; és &tex;\displaystyle 0\le y_1\le \dots\le y_n&xet; nemnegatív számokat, amikre &tex;\displaystyle a_i=K-x_i&xet; és &tex;\displaystyle b_i=K+y_i&xet;.

A baloldalt alulról becsüljük így:

&tex;\displaystyle (a_1+\dots+a_n+b_1+\dots+b_n)^2 = \big(2nK+(-x_1-\dots-x_n+y_1+\dots+y_n)\big)^2 \ge &xet;

&tex;\displaystyle \ge (2nK)^2 + 4nK(-x_1-\dots-x_n+y_1+\dots+y_n) = 4nK(nK-x_1-\dots-x_n+y_1+\dots+y_n). &xet;

(1)

A jobboldalon álló tagokra azt a felső becslést írjuk fel, hogy

&tex;\displaystyle a_ib_i = (K-x_i)(K+y_i) = K^2-Kx_i+Ky_i - x_iy_i \le K(K-x_i+y_i). &xet;

(2)

Ha ezt minden &tex;\displaystyle i&xet;-re összegezzük, azt kapjuk, hogy

&tex;\displaystyle a_1b_1+\dots+a_nb_n \le K(nK-x_1-\dots-x_n+y_1+\dots+y_n). &xet;

Így hát

&tex;\displaystyle (a_1+\dots+a_n+b_1+\dots+b_n)^2 \ge 4nK(nK-x_1-\dots-x_n+y_1+\dots+y_n) \ge 4n(a_1b_1+\dots+a_nb_n). &xet;

Egyenlőség akkor állhat fenn, ha (1)-ben &tex;\displaystyle x_1+\dots+x_n=y_1+\dots+y_n&xet;, másrészt (2)-ben &tex;\displaystyle x_i&xet; és &tex;\displaystyle y_i&xet; közül legalább az egyik &tex;\displaystyle 0&xet;. Az &tex;\displaystyle x_i&xet;-k és az &tex;\displaystyle y_i&xet;-k sorrendje miatt az utóbbi azt jelenti, hogy az &tex;\displaystyle x_1,\dots,x_n,y_1,\dots,y_n&xet; számok között van legalább &tex;\displaystyle n&xet; darab szomszédos &tex;\displaystyle 0&xet;. Visszaírva az eredeti számokra: az &tex;\displaystyle a_1,\dots,a_n,b_1,\dots,b_n&xet; számok átlaga &tex;\displaystyle K&xet;, továbbá a számok között legalább &tex;\displaystyle n&xet; darab (szomszédos) egyenlő &tex;\displaystyle K&xet;-val.

Előzmény: [730] Erben Péter, 2013-12-13 15:21:50

[730] Erben Péter	2013-12-13 15:21:50
A mintamegoldások nem foglalkoztak azzal, mikor áll egyenlőség az 5. feladatban. Pedig érdekes.
Előzmény: [726] Erben Péter, 2013-12-01 13:45:56

[729] Erben Péter	2013-12-13 15:20:55
Talán onnan lehet sejteni, hogy címkézett csúcsú "gráfról" van szó, hogy ellenkező esetben izomorfia szerint kellene csoportosítani a lehetséges kapcsolati hálózatokat, az pedig viszonylag ismert, hogy a gráf-izomorfia eldöntése nehéz. (http://en.wikipedia.org/wiki/Graph_isomorphism_problem)
Előzmény: [728] n, 2013-12-02 19:08:26

[728] n	2013-12-02 19:08:26
Megjegyzés: a 4-es feladatnál az emberek megkülönböztethetők (volt, aki másképp értette), különben amúgy - lényegileg - az A002854 OEIS-es sorozatot kapnánk (csak az 1., 3., 5., stb. tagokat 0-ra cserélve), amire viszont nincs (legalábbis én nem tudok ilyenről) szép képlet.
Előzmény: [726] Erben Péter, 2013-12-01 13:45:56

[727] jonas	2013-12-01 19:21:50
Érdekes feladatok, köszönöm, hogy beírtad őket.
Előzmény: [726] Erben Péter, 2013-12-01 13:45:56

[726] Erben Péter

2013-12-01 13:45:56

Az idei specmatos 1. forduló:

1. A P pont végigfut egy kör félkörnél rövidebb AB ívén. Legyen P' a P-vel átellenes pont a körön. Bizonyítsuk be, hogy AP'^.BP'-AP^.BP állandó.

2. Hány N pozitív egészre teljesül, hogy N/5 egy egész szám hetedik, N/7 pedig egy egész szám ötödik hatványa?

3. Legyen P az ABC szabályos háromszög belső pontja, továbbá A₁, B₁ és C₁ a P pont merőleges vetülete rendre a BC, CA, illetve AB oldalon. Bizonyítsuk be, hogy

AC₁^.BA₁+BA₁^.CB₁+CB₁^.AC₁=C₁B^.A₁C+A₁C^.B₁A+B₁A^.C₁B.

4. Adott n ember között hányféle olyan ismeretségi kapcsolatrendszer lehet, hogy mindenki páratlan sok másikat ismer (az ismeretség kölcsönös)?

5. Legyenek a₁ $\le$ a₂ $\le$ ... $\le$ a_n $\le$ b₁ $\le$ b₂ $\le$ ... $\le$ b_n valós számok. Bizonyítsuk be, hogy

(a₁+a₂+...+a_n+b₁+b₂+...+b_n)² $\ge$ 4n(a₁b₁+a₂b₂+...+a_nb_n).

[725] w	2013-03-12 19:57:41
Túl könnyű egy Varga Tamás-verseny döntőre.
Előzmény: [724] Fálesz Mihály, 2013-03-12 17:52:33

[724] Fálesz Mihály	2013-03-12 17:52:33
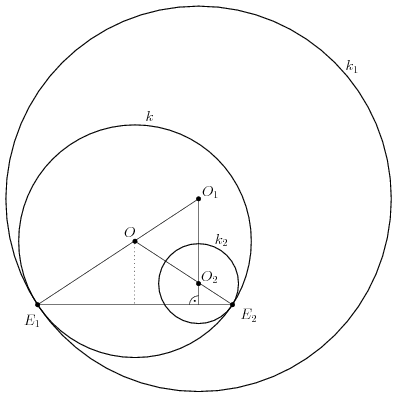
Szerintem az 1. feladat túl könnyű egy spec.matos OKTV döntőre. OE₁=OE₂=r, O₁E₁=r₁, O₂E₂=r₂. Az E₁E₂O háromszög egyenlő szárú, az O₁O₂ szakasz merőleges az E₁E₂ alapra. Ebből következik, hogy az OO₁O₂ háromszög is egyenlő szárú: OO₁=OO₂. Így hát r₁-r=O₁E₁-OE₁=O₁O=OO₂=OE₁-O₂E₂=r-r₂, $r = \frac{r_1+r_2}2.$

Előzmény: [721] Erben Péter, 2013-03-11 22:14:18

[723] Fálesz Mihály

2013-03-12 17:39:54

A 2. feladat teleszkópos összeggel:

$\sum_{k=1}^m\frac{m(m-1)(m-2)\dots(m-k+1)k}{m^{k+1}}=$

$=\sum_{k=1}^m\left(\frac{m(m-1)(m-2)\dots(m-k+1)}{m^k}- \frac{m(m-1)(m-2)\dots(m-k)}{m^{k+1}}\right) = 1-0.$

Előzmény: [722] Róbert Gida, 2013-03-12 17:04:23

[722] Róbert Gida	2013-03-12 17:04:23
2. feladat kombinatorikus megoldása (m>0 egészre): bizonyítandó nyilván ekvivalens ezzel: 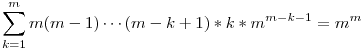$\sum _{k=1}^m m(m-1)\cdots (m-k+1) km^{m-k-1}=m^m$ . Vegyünk m tárgyat, és ezt szeretnénk m színnel kiszínezni, hányféleképpen tehetjük ezt meg? Trivi: m^m féleképpen, hiszen minden tárgyat m féleképpen színezhetünk. Máshogy megszámolva: tegyük fel, hogy az első k tárgy színe mind különböző, de ez (k+1)-re már nem igaz, ekkor m(m-1)^...(m-k+1) féle választás van az első k tárgy színezésére, k lehetőség a k+1-dikre, míg m^m-k-1 a többire. És szorozni kell a lehetőségeket. Itt k mehet 1-től m-ig, továbbá minden színezést pontosan egyszer számoltunk.
Előzmény: [721] Erben Péter, 2013-03-11 22:14:18

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?