| [36] marcius8 | 2014-12-10 10:11:12 |
 Az alábbi táblázat mutatja, hogy ha az &tex;\displaystyle ABC&xet; háromszög oldalát &tex;\displaystyle n&xet; egyenlő részre osztjuk fel, akkor hány esetben metszik egymást egy pontban az &tex;\displaystyle AA_1&xet;, &tex;\displaystyle BB_1&xet;, &tex;\displaystyle CC_1&xet; egyenesek. (A metszéspontok számát nagyobb &tex;\displaystyle n&xet; értékekre is meghatároztam.) Sejtésem, hogy ha &tex;\displaystyle n&xet; páratlan prím hatványa, akkor nincs metszéspont. Felhasználtam, hogy a Ceva-tétel szerint az &tex;\displaystyle AA_1&xet;, &tex;\displaystyle BB_1&xet;, &tex;\displaystyle CC_1&xet; egyenesek pontosan akkor metszik egymást egy pontban, ha a következő egyenlet teljesül:&tex;\displaystyle \frac{AB_1}{B_1C}*\frac{BC_1}{C_1A}*\frac{CA_1}{A_1B}=1&xet;
| n |
metszéspontok száma |
n |
metszéspontok száma |
n |
metszéspontok száma |
n |
metszéspontok száma |
| 1 |
0 |
2 |
1 |
3 |
0 |
4 |
7 |
| 5 |
0 |
6 |
13 |
7 |
0 |
8 |
19 |
| 9 |
0 |
10 |
25 |
11 |
0 |
12 |
31 |
| 13 |
0 |
14 |
37 |
15 |
6 |
16 |
43 |
| 17 |
0 |
18 |
49 |
19 |
0 |
20 |
61 |
| 21 |
0 |
22 |
61 |
23 |
0 |
24 |
91 |
| 25 |
0 |
26 |
73 |
27 |
0 |
28 |
79 |
| 29 |
0 |
30 |
91 |
31 |
0 |
32 |
91 |
| 33 |
0 |
34 |
97 |
35 |
12 |
36 |
103 |
| 37 |
0 |
38 |
109 |
39 |
0 |
40 |
133 |
| 41 |
0 |
42 |
133 |
43 |
0 |
44 |
127 |
| 45 |
42 |
46 |
133 |
47 |
0 |
48 |
187 |
| 49 |
0 |
50 |
145 |
51 |
0 |
52 |
151 |
| 53 |
0 |
54 |
157 |
55 |
12 |
56 |
175 |
| 57 |
0 |
58 |
169 |
59 |
0 |
60 |
235 |
| 61 |
0 |
62 |
181 |
63 |
48 |
64 |
187 |
| 65 |
6 |
66 |
205 |
67 |
0 |
68 |
199 |
| 69 |
0 |
70 |
229 |
71 |
0 |
72 |
283 |
| 73 |
0 |
74 |
217 |
75 |
6 |
76 |
223 |
| 77 |
12 |
78 |
235 |
79 |
0 |
80 |
325 |
| 81 |
0 |
82 |
241 |
83 |
0 |
84 |
283 |
| 85 |
6 |
86 |
253 |
87 |
0 |
88 |
271 |
| 89 |
0 |
90 |
331 |
91 |
12 |
92 |
271 |
| 93 |
0 |
94 |
277 |
95 |
0 |
96 |
343 |
| 97 |
0 |
98 |
289 |
99 |
24 |
100 |
301 |
| 101 |
0 |
102 |
301 |
103 |
0 |
104 |
319 |
| 105 |
90 |
106 |
313 |
107 |
0 |
108 |
319 |
| 109 |
0 |
110 |
349 |
111 |
0 |
112 |
439 |
| 112 |
439 |
113 |
0 |
113 |
0 |
114 |
337 |
| 114 |
337 |
115 |
0 |
115 |
0 |
116 |
343 |
| 116 |
343 |
117 |
12 |
117 |
12 |
118 |
349 |
| 118 |
349 |
119 |
12 |
119 |
12 |
120 |
559 |
| 121 |
0 |
122 |
361 |
123 |
0 |
124 |
367 |
| 125 |
0 |
126 |
457 |
127 |
0 |
128 |
379 |
| 129 |
0 |
130 |
403 |
131 |
0 |
132 |
415 |
| 133 |
0 |
134 |
397 |
135 |
66 |
136 |
409 |
| 137 |
0 |
138 |
409 |
139 |
0 |
140 |
541 |
| 141 |
0 |
142 |
421 |
143 |
24 |
144 |
583 |
| 145 |
0 |
146 |
433 |
147 |
0 |
148 |
439 |
| 149 |
0 |
150 |
451 |
151 |
0 |
152 |
463 |
| 153 |
12 |
154 |
481 |
155 |
0 |
156 |
493 |
| 157 |
0 |
158 |
469 |
159 |
0 |
160 |
613 |
| 161 |
12 |
162 |
481 |
163 |
0 |
164 |
487 |
| 165 |
90 |
166 |
493 |
167 |
0 |
168 |
679 |
| 169 |
0 |
170 |
523 |
171 |
12 |
172 |
511 |
| 173 |
0 |
174 |
517 |
175 |
66 |
176 |
571 |
| 177 |
0 |
178 |
529 |
179 |
0 |
180 |
751 |
| 181 |
0 |
182 |
565 |
183 |
0 |
184 |
547 |
| 185 |
0 |
186 |
553 |
187 |
12 |
188 |
559 |
| 189 |
60 |
190 |
577 |
191 |
0 |
192 |
631 |
| 193 |
0 |
194 |
577 |
195 |
132 |
196 |
583 |
| 197 |
0 |
198 |
637 |
199 |
0 |
200 |
619 |
| 201 |
0 |
202 |
601 |
203 |
6 |
204 |
631 |
| 205 |
0 |
206 |
613 |
207 |
12 |
208 |
655 |
| 209 |
24 |
210 |
847 |
211 |
0 |
212 |
631 |
| 213 |
0 |
214 |
637 |
215 |
0 |
216 |
739 |
| 217 |
0 |
218 |
649 |
219 |
0 |
220 |
721 |
| 221 |
24 |
222 |
661 |
223 |
0 |
224 |
823 |
| 225 |
78 |
226 |
673 |
227 |
0 |
228 |
691 |
| 229 |
0 |
230 |
697 |
231 |
144 |
232 |
691 |
| 233 |
0 |
234 |
739 |
235 |
0 |
236 |
703 |
| 237 |
0 |
238 |
733 |
239 |
0 |
240 |
1111 |
| 241 |
0 |
242 |
721 |
243 |
0 |
244 |
727 |
| 245 |
12 |
246 |
733 |
247 |
24 |
248 |
739 |
| 249 |
0 |
250 |
745 |
251 |
0 |
252 |
967 |
| 253 |
0 |
254 |
757 |
255 |
48 |
256 |
763 |
|
|
| Előzmény: [35] w, 2014-02-11 10:54:03 |
|
| [35] w | 2014-02-11 10:54:03 |
 Adott az ABC háromszög, és az n>1 egész szám. Az ABC háromszög mindegyik oldalát n egyenlő részre osztottuk. Kijelöltük a BC, CA, AB oldalakon egy-egy osztópontot, ezek rendre A1, B1 és C1. Mely n-ekre lehetséges, hogy AA1, BB1 és CC1 egyenesek egy ponton menjenek át? Határozzuk meg n függvényében annak valószínűségét, hogy az AA1, BB1, CC1 egyenesek egy ponton menjenek át.
|
|
| [34] marcius8 | 2014-02-06 12:53:17 |
 Köszönöm az értékes táblázatot! Sajnos nekem is csak számítógéppel sikerült ilyen háromszöget generálni. De még arra is gondoltam, hogy érdemes olyan (szokásos jelölésekkel) "ABC" háromszöget keresni, amelyben a szögek felének koszinusza racionális szám. Ha van ilyen háromszög, akkor van olyan háromszög is, amelyben az oldalak hossza is racionális és a szögfelezők hossza is racionális. Tisztelettel: Bertalan Zoltán.
|
| Előzmény: [30] aaaa, 2014-02-05 14:26:27 |
|
| [33] marcius8 | 2014-02-06 12:46:51 |
 Köszönöm az 1. kérdésemre adott megoldást. nekem másképp sikerült a nemlétezést bizonyítani, lényegesen bonyolultabban. Az itt leírt megoldás bizonyítás lényegesen egyszerűbb. (Nekem sikerült felhasználni azt a tételt, hogy két egész szám negyedik hatványának összege nem lehet egy egész szám negyedik hatványa.) Tisztelettel: Bertalan Zoltán.
|
| Előzmény: [29] aaaa, 2014-02-05 13:28:37 |
|
| [32] aaaa | 2014-02-05 21:09:44 |
 Újabb helyesbítés: a legkisebb egész megoldás a (975,975,546) lesz, a legkisebb nem egyenlőszárú pedig az (5686681,4206125,2826516) háromszög lesz (az eddig megtaláltak alapján, lehet, hogy létezik kisebb).
|
| Előzmény: [30] aaaa, 2014-02-05 14:26:27 |
|
|
| [30] aaaa | 2014-02-05 14:26:27 |
 2-höz vegyük észre, hogy elég, ha a szögfelezők racionális hosszúak, ekkor egy nagyítással egész hosszút kaphatunk belőle. Ismeretes, hogy a szögfelezők hossza: 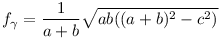 , innét számítógéppel kerestem olyanokat, ahol mindhárom szögfelező racionális hosszú. Ha a , innét számítógéppel kerestem olyanokat, ahol mindhárom szögfelező racionális hosszú. Ha a b b c, akkor 200 c, akkor 200 b esetén a következők jók: b esetén a következők jók:
| a |
b |
c |
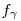 |
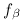 |
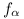 |
| 25 |
25 |
14 |
24 |
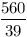 |
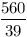 |
| 50 |
50 |
28 |
48 |
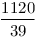 |
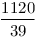 |
| 75 |
75 |
42 |
72 |
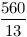 |
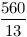 |
| 100 |
100 |
56 |
96 |
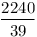 |
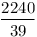 |
| 125 |
125 |
70 |
120 |
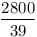 |
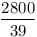 |
| 169 |
125 |
84 |
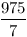 |
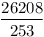 |
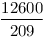 |
| 150 |
150 |
84 |
144 |
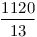 |
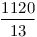 |
| 175 |
175 |
98 |
168 |
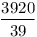 |
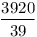 |
| 200 |
200 |
112 |
192 |
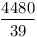 |
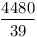 |
| 169 |
154 |
125 |
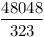 |
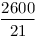 |
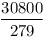 |
| 275 |
169 |
150 |
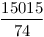 |
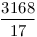 |
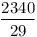 |
| 238 |
169 |
169 |
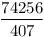 |
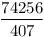 |
120 |
|
Ebből látszik, hogy a legkisebb ilyen ezek közül a (936,560,560) oldalú lesz, a talált legkisebb, nem egyenlőszárú a (4686825,3485664,2028600) oldalakkal rendelkező
|
| Előzmény: [28] marcius8, 2014-02-04 13:12:38 |
|
| [29] aaaa | 2014-02-05 13:28:37 |
 4.-esre 3,4 oldalú téglalap jó.
1-essel a következőre jutottam: Bicentrikus négyszögben 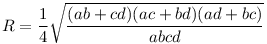 , , 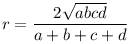 , szimmetrikus trapéznál az oldalhosszak pedig , szimmetrikus trapéznál az oldalhosszak pedig 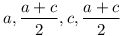 . Némi egyszerűsítés után adódik, hogy . Némi egyszerűsítés után adódik, hogy 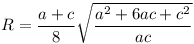 , , 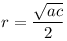 . .
Vagyis r egész voltából adódik, hogy a= e2a12, c= e2a12, c= e2c12 alakba írható, ahol (a,c)= e2c12 alakba írható, ahol (a,c)= e2, e2,  négyzetmentes, és (a1,c1)=1 Ezekkel a jelölésekkel élve: négyzetmentes, és (a1,c1)=1 Ezekkel a jelölésekkel élve:
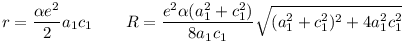
Tehát a12+c12,2a1c1 egy Pithagoraszi számhármas két tagja. (a12+c12,2a1c1)=((a1+c1)2,2a1c1)=f|2 miatt tehát két eset van:
a) Ha f=1, akkor: a12+c12=u2-v2, a1c1=uv, mert 2|uv. Ebből adódik, hogy 2|v, mert a12+c12+v2=u2. A négyszám-tétel alapján ekkor u=xy, v=zw, a1=xz, c1=yw, ahol ezek a számok páronként relatív prímek a feltételeink miatt. Legyen mondjuk z páros, ez felthető. Ekkor
v2+a12+c12-u2=w2(y2+z2)+x2(z2-y2)=0
w2(y2+z2)=x2(y2-z2)
, innét pedig a relatív prímségek miatt, és (2,x)=1 miatt adódik, hogy
y2-z2=w2 y2+z2=x2
Ami lehetetlen, mert két négyzetszám összege és különbsége egyszerre nem lehet négyzetszám. Vagyis ilyenkor nincs megoldás.
b) b) Ha f=2, akkor a1c1=u2-v2=(u-v)(u+v), a12+c12=uv innét az előbbi alapján: u+v=xy, u-v=zw, a1=xz, c1=yw, innét 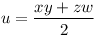 , , 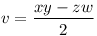 . Ebből kapjuk, hogy: x2(y2-4z2)=w2(4y2+z2), innét a relatív prímségből (y2-4z2,4y2+z2)|17 miatt a következő esetek lehetségesek: y2-4z2=w2, 4y2+z2=x2 vagy 17w2=y2-4z2, 17x2=4y2+z2, ahol x,y,z,w páronként relatív prímek. . Ebből kapjuk, hogy: x2(y2-4z2)=w2(4y2+z2), innét a relatív prímségből (y2-4z2,4y2+z2)|17 miatt a következő esetek lehetségesek: y2-4z2=w2, 4y2+z2=x2 vagy 17w2=y2-4z2, 17x2=4y2+z2, ahol x,y,z,w páronként relatív prímek.
y2-4z2=w2
16y2+4z2=4x2
4y2-16z2=4w2
4y2+z2=x2
Innét x2-4w2=17z2 és 4x2+w2=17y2, szóval a két egyenletpár lényegében ekvivalens egymással. Elég tehát csak az egyiket vizsgálni. Tegyük fel, hogy találtunk egy megoldást, ahol mind a 4 változó páratlan, és páronként relatív prímek. De ekkor z2+4y2=x2 miatt ez egy relatív prím pitagoraszi számhármas, így 2y=2uv, de y páratlan, uv nem, ez ellentmondás. Ekkor sincs megoldás.
|
| Előzmény: [28] marcius8, 2014-02-04 13:12:38 |
|
| [28] marcius8 | 2014-02-04 13:12:38 |
 Tulajdonképpen ez a témakör tökéletesen alkalmas arra, hogy a különböző geometriai indittatású diofantoszi egyenletek megoldását itt megvitassuk. Íme néhány példa:
1. Keressünk olyan szimmetrikus érintőtrapézt, amelynek oldalhosszai, köré írt körének sugara és beírt körének sugara egész számok.
2. Keressünk olyan háromszöget, amelynek oldalainak hossza és belső szögfelezőinek hossza egész számok.
3. Keressünk olyan háromszöget, amelynek oldalainak hossza, belső szögharmadolóinak hossza és a csúcsokból kiinduló belső szögharmadolók által a csúcsokkal szemközti oldalakból kimetszett szakaszok hossza egész számok.
4. Keressünk paralelogrammát, amelynek oldalainak hossza és átlóinak hossza egész számok.
|
|
| [27] marcius8 | 2014-01-31 13:10:14 |
 Korábban már felvetettem a következő problémát Ki tud ebben segíteni?
Középiskolában tanítok matematikát, és például geometriai feladatok akkor könnyen megoldhatóak illetve a geometriai feladatok megoldásai akkor javíthatóak könnyen, ha a feladatok adatai és eredményei egész számok. Például szerencsés olyan derékszögű háromszöggel számolni, amelynek oldalai egész számok --> pitagoraszi számhármasok. A feladat a következő: Keressünk olyan derékszögű tetraédert, amelynek minden éle egész szám. (Egy tetraéder akkor derékszögű, ha van olyan csúcsa, amelyből kiinduló három él páronként egymásra merőleges.) Számítógéppel ilyent könnyű találni: Az "OABC" tetraéder "O" csúcsából kiinduló élek páronként merőlegesek egymásra, és OA=44, OB=117, OC=240, ekkor AB=125, BC=267, CA=244. Lehet ezeket a tetraédereket úgy generálni, mint a pitagoraszi számhármasokat?
Lehetne esetleg úgy meghatározni az "OA", "OB", "OC", "a=BC", "b=CA", "c=AB" szakaszok hosszát, úgy hogy azok egész számok legyenek, de az "OA", "OB", "OC" szakaszok egymással páronként 120°-os szöget zárjanak be? ekkor az "O" pont az "ABC" háromszög izogonális pontja. (Számítógéppel találtam ilyen szakaszokat, tehát biztos hogy van megoldás. De hogyan lehet ilyen megoldásokat még generálni?)
Tisztelettel: Bertalan Zoltán.
|
|
|
|
|
| [23] rizsesz | 2009-03-20 15:52:43 |
 Innen meg már a lineáris megoldás is könnyen jön:
Ha (x;y) jó, akkor (3y-x;y) is; ez pedig könnyen látható, hogy a kezdőérték jó megválasztásával csupa különböző megoldást ad.
|
| Előzmény: [21] Sirpi, 2009-03-20 14:54:12 |
|
| [22] rizsesz | 2009-03-20 15:46:31 |
 Ami gyanúsan látszik, hogy akár már 1 szám rögzítése mellett is végtelen sok megoldás van. Arra gondolok, hogy x = 1 mellett az 1 + x2 + y2 = 3xy egyenletet kielégíti az (x;y) pár, akkor kielégíti az (x,;y,) pár is, ahol (x,;y,) például valamilyen lineáris függvénnyel származtatható az (x;y) párból.
A párhuzamos ötlet a Fibonacci-sorozat elemeivel: (x;y)=(F2k-1;F2k+1), és ezt indukcióval igazolni már könnyű is:
Legyen valamely n számra (pl n = 1 esetén igaz): Fn2 + Fn+22 + 1 = 3 * Fn *Fn+2
Az indukciós lépésben igazoljuk, hogy ez akkor igaz n helyett n + 2 -re is:
Fn+42 + Fn+22 + 1 = 3 * Fn+4 *Fn+2
A két egyenlet különbsége: Fn+42 - Fn2 = 3 * (Fn+4 - Fn)*Fn+2
(Fn+4 - Fn)-gyel leosztva: Fn+4 + Fn = 3 * Fn+2, ez pedig igaz, mert Fn+4 + Fn = Fn+3 + Fn+2 + Fn = 2 * Fn+2 + Fn+1 + Fn= 3 * Fn+2
|
| Előzmény: [21] Sirpi, 2009-03-20 14:54:12 |
|
| [21] Sirpi | 2009-03-20 14:54:12 |
 Igen :-) és tudom, akárhogy folytatódhatna a sorozat, de igazából úgy folytatódik, ahogy elkezdődött. Egyébként ha már kitaláltuk, mi a feladat, bizonyítsuk be, hogy az egyenletnek végtelen sok pozitív egész megoldása van (ebben a lista is segíthet).
|
| Előzmény: [20] rizsesz, 2009-03-20 13:12:13 |
|
|
| [19] Sirpi | 2009-03-20 09:20:01 |
 Na, akkor egy kis segítség: a 3-mal felszorzott számok megoldásai egy f(a,b,c)=g(a,b,c) egyenletnek, ahol f és g szép, egyszerű függvények. Ezek a számok pedig az f(a,b,c)=3g(a,b,c) egyenletnek megoldásai. És igazából az egyik függvény miatt nem véletlen, hogy a pitagoraszi számhármasokhoz raktam be a listát...
|
| Előzmény: [18] Sirpi, 2009-03-19 14:56:36 |
|
| [18] Sirpi | 2009-03-19 14:56:36 |
 Tudom, nem teljesen a témába vág, de még mindig ez volt a legközelebbi téma, amit találtam. A kérdés, hogy mi a közös a következő számhármasokban (a lista persze nem teljes):
Egyébként igazán úgy lenne teljesen korrekt, ha minden számot felszoroznék hárommal (tehát 3 3 3, 3 3 6 stb.) de úgyis mindenki fejben visszaosztaná, mert így könnyebb átlátni, szóval azért választottam a 3-mal leosztott listát.
|
 |
|
| [17] Kóta Béla | 2008-03-09 21:42:00 |
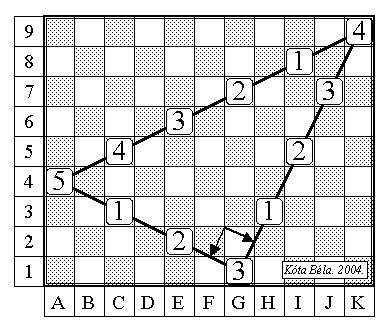
 A tejesség kedvéért. "A Piramisok Tanulsága" dolgozatomhoz összegyűjtöttem 58 hivatkozott irodalmi forrást. Ezeknek az ókori matematikatörténettel is foglalkozó fele egyhangúan állítja, hogy az óegyiptomiak nem ismertél a Pitagorasz tételt. Erre hivatkozva tagadják azt is, hogy használhattak a derékszögek kijelölésére 3-4-5 oldalarányú háromszöget (vagy 12 csomós zsinórt). Erre a 9 × 11 kockás sakktábla szerű négyzethálóra ránézve -- Pitagorasz tétel nélkül is -- belátható, hogy a 3-4-5 oldalarányú háromszög valóban derékszögű.
Induljunk el az A4 kockából HÁROM -1/+2 irányú lóugrással a G1 kockáig. A G1 kockából NÉGY +2/+1 irányú lépéssel eljutunk a K9 sarokba. A K9 sarokból ÖT -1/-2 lóugrással visszaérünk a kiindulási A4 kockába.
Nagyobb táblán, más arányú "lóugrásokkal" az összes Pitagoraszi számhármas kisakkozható.
|
 |
| Előzmény: [16] Kóta Béla, 2008-03-07 23:10:09 |
|
| [16] Kóta Béla | 2008-03-07 23:10:09 |
 Válasz: onnan tudjuk, hogy a félszög tangense racionális mert két természetesm szám y/x hányadosa. A számelméletes levezetés pl - Ja. I. PERELMAN: Szórakoztató algebra. 147-151.o.
Én még maradok a QBasic nyelvnél:
DEFINT A-Z
FOR x = 2 TO 10: FOR y = 1 TO x - 1
a = x * x - y * y: b = 2 * x * y: c = x * x + y * y
PRINT x; y, a; b; c
NEXT y: NEXT x
END
Itt a számhármasok akkor relatív primek, ha x és y közül az egyik páros, a másik páratlan (?).
|
| Előzmény: [15] Fálesz Mihály, 2008-03-07 15:14:04 |
|
| [15] Fálesz Mihály | 2008-03-07 15:14:04 |
 Elnézést a kötekedésért, de szerintem, ha ezt a megoldást tisztességesen leírjuk, nem lesz sokkal kevesebb számelmélet benne, mint a tankönyvi módszerben. (Azt viszont elismerem, hogy ebből az ötletből egy lényegesen különböző megoldást lehet összerakni.)
A megoldás több ponton is kiegészítésre szorul.
Először is, honnan tudjuk, hogy a fél szög tangense racionális? Én ezt onnan látom, hogy 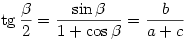 , vagyis trigonometrikus azonosságot használok. (Vagy a szögfelező és a körülírt kör metszéspontját írom fel a befogók által meghatározott koordináta-rendszerben, ami lényegében ugyanaz.) , vagyis trigonometrikus azonosságot használok. (Vagy a szögfelező és a körülírt kör metszéspontját írom fel a befogók által meghatározott koordináta-rendszerben, ami lényegében ugyanaz.)
Másodszor, az a:b:c=(x2-y2):2xy:(x2+y2) aránypárból miért következtethetünk arra, hogy a=x2-y2, b=2xy és c=x2+y2? Ezt csak akkor tehetjük meg, ha tudjuk, hogy az x2 y2 és 2xy számok relatív prímek, ami akkor igaz, ha x és y ellentétes paritásúak, a b oldal pedig osztható 4-gyel. y2 és 2xy számok relatív prímek, ami akkor igaz, ha x és y ellentétes paritásúak, a b oldal pedig osztható 4-gyel.
Harmadszor, egy apróság: az ábrán a középső háromszög felnagyítva szerepel, az oldalai az,bz,cz, ahol 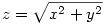 . .
A teljes megoldás menete tehát valami ilyesmi lehetne.
1. Bebizonyítjuk, hogy a fél hegyesszögek tangensei racionálisak.
2. Bebizonyítjuk, hogy valamelyik befogó osztható 4-gyel, a másik kettő páratlan.
3. Felrajzoljuk az ábrát, és leolvassuk, hogy a:b:c=(x2-y2):2xy:(x2+y2).
4. Megállapítjuk, hogy mivel b osztható 4-gyel, x és y közül az egyik páros, ezért x2 y2 páratlan. y2 páratlan.
5. Megállapítjuk, hogy az x2 y2 és 2xy számoknak nem lehet közös prímosztója: sem a 2, sem más. y2 és 2xy számoknak nem lehet közös prímosztója: sem a 2, sem más.
6. Most már tudjuk, hogy mindkét számhármasban olyan pozitív egészek vannak, amiknek a legnagyobb közös osztója 1, tehát a két számhármas ugyanaz.
F.M.
|
| Előzmény: [14] Kóta Béla, 2008-03-06 21:27:58 |
|
| [14] Kóta Béla | 2008-03-06 21:27:58 |
 A Pitagoraszi számhármasok számelmélet-mentes levezetése az alábbi ábra szerint:
Egy derékszögű háromszöget zárjunk körül egy téglalappal úgy, hogy a háromszög egyik hegyesszögének szögfelezője legyen párhuzamos a téglalap egyik oldalával. A félszög tangense két természetes szám hányadosa = y/x, ahol x > y. A többi gyalog algebra... Természetesen a b = 2xy mindig páros.
|
| Előzmény: [13] Kóta Béla, 2008-03-06 21:14:22 |
|
|
|
