Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48]

Szeretnél hozzászólni? Jelentkezz be.

[136] Iván88	2006-01-15 19:39:47
Na most aztán teljesen kifogytam az ötletekből. Lőjük le a megoldást, mert más feladatokról is szeretnék beszélni.
Előzmény: [135] nadorp, 2006-01-11 08:32:32

[135] nadorp	2006-01-11 08:32:32
Még nem,de majdnem. Tehát legyen a₁=1 és a_k=k^.(k-1)^-1, ha 2 $\leq$ k $\leq$ p-1. Ez jónak tűnik, mert a₁...a_k $\equiv$ k mod(p),hiszen k kivételével mindegyik tag inverze is szerepel a szorzatban. Már csak annak a bizonyítása van hátra, hogy ezek a számok különböző maradékot adnak p-vel osztva. Ehhez azt kell belátni, hogy egyrészt az 1 maradék csak egyszer fordul elő, másrészt, hogy az n^.(n-1)^-1 $\equiv$ k^.(k-1)^-1 mod(p) (2 $\leq$ n,k $\leq$ p-1) kongruenciának csak n=k a megoldása. ( az esetszétválasztás azért kell, mert 0-nak nincs inverze).
Előzmény: [134] Iván88, 2006-01-10 20:26:18

[134] Iván88	2006-01-10 20:26:18
Ha jól veszem ki, akkor x=3^-1, de ebben nem vagyok ebben biztos. Eszerint az a_k=k^.(k-1)^-1, de ezzel még nem vagyok kész-szerintem.
Előzmény: [133] nadorp, 2006-01-09 08:43:04

[133] nadorp

2006-01-09 08:43:04

Induljunk ki a Te megoldásodból.Ebben 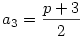$a_3=\frac{p+3}2$ .Ekkor

2a₃=p+3,azaz

2a₃ $\equiv$ 3 mod(p).

Ha most a 2 inverzét ( lásd 125. hozzászólás) jelöli 2^-1, akkor

a₃ $\equiv$ 3^.2^-1 mod(p). Ez egy "szebb" alak,mert általánosítható. Legyen

a₁=1 a₂=2^.1 a₃=3^.2^-1 a₄=4x... Mi az x ? Folytasd a sorozatot.

Előzmény: [132] Iván88, 2006-01-08 16:55:16

[132] Iván88	2006-01-08 16:55:16
Sokat gondolkoztam ezen, de nem találtam meg az ehhez szükséges infókat, magamtól meg egyszerűen képtelen vagyok rájönni.
Előzmény: [131] nadorp, 2005-12-30 20:38:32

[131] nadorp	2005-12-30 20:38:32
Ígéretes elindulás. Általában is igaz, hogy megválasztható a sorrend úgy, hogy a₁a₂...a_k p-vel osztva k-t ad maradékul. Ehhez a konstrukcióhoz minden információ a rendelkezésedre áll a korábbi hozzászólások alapján.
Előzmény: [130] Iván88, 2005-12-30 18:29:22

[130] Iván88	2005-12-30 18:29:22
Egy kicsit kanyarodjunk vissza a B. 3859-re. Az már volágos, hogy (p-1)!+1 osztható p-vel. Ha a sejtésem igaz, akkor a₂=2 és a₃=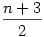 $\frac{n+3}2$ , egyellőre kifogytam az ötletekből, de hátha halakit ez elindít(ott).
Előzmény: [121] Iván88, 2005-12-24 23:14:03

[129] Geg

2005-12-29 14:59:25

A feladatot en javitottam, volt nehany ember, aki hasonloan igyekezett megkozeliteni a feladatot, de csak 1 vagy 2 volt az aki tisztessegesen vegigszamolta geometriaval az egeszet.

Lenyegesen egyszerubb megoldas ha vektorokat hasznalunk: fel kell irni a mozgasegyenletet tetszoleges testnek ugy, hogy az origo a tkp (hiszen nyilvan ekorul forog a rendszer ha a testek egymastol mert tavolsaga idoben allando), ekkor nehany egyszeru atalakitas soran kijon a szogsebesseg es az, hogy az nem fugg az eppen aktualis test tomegetol, csak az ossztomegtol.

Előzmény: [126] lorantfy, 2005-12-28 23:12:10

[128] lorantfy	2005-12-29 11:14:31
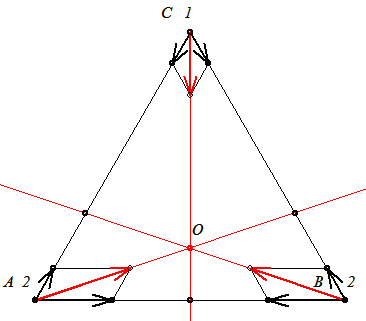
Szia Viktor! A szöveg azt mondja, hogy "bármely kettő közötti távolság megegyezik". Ez a te példád esetében csak úgy lehetne, ha az első két tömegpont egyenlő, a 3. pedig az őket összekötő szakasz felező merőlegesén van úgy, hogy egyenlő oldalú $\Delta$ -t alkossanak. A forgáspont akkor sem lehet az első kettő tömegközéppontjában, mert a grav. erők eredőinek hatásvonalai nem ott metszik egymást.

Előzmény: [127] xviktor, 2005-12-29 01:01:02

[127] xviktor

2005-12-29 01:01:02

Olyan is lehet-e a rendszer, hogy 2 forog egy pont korul atellenben, a 3. meg a ketto sulypontja korul, a masik kettot osszekoto szakaszra meroleges sugarral?

Udv: Viktor

Előzmény: [126] lorantfy, 2005-12-28 23:12:10

[126] lorantfy	2005-12-28 23:12:10
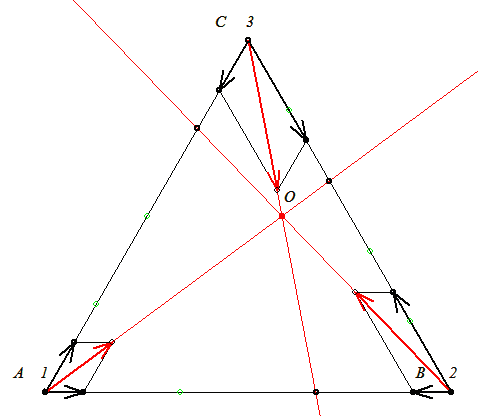
Szia X! P. 3833. Mozoghat-e három különböző tömegű pontszerű test egymás gravitációs terében úgy, hogy bármely kettő közötti távolság megegyezik és a mozgás során állandó marad? Mekkora szögsebességgel forog ez a rendszer? A második kérdés sugallja a választ az elsőre. Forgatni kell a rendszert, méghozzá úgy, hogy a testekre ható gravitációs erők eredője éppen a körmozgást biztosító centripetális erő legyen. A testek egy egyenlő oldalú háromszög csúcspontjaiban vannak. Először keressül meg a forgás középpontját. A testekre ható grav. erők eredőit meghosszabbítva ezek egy pontban metszik egymást, (ugyanis vektori eredőjük nulla, hiszen a komponensek összege is nulla) csak ez a pont lehet a forgás középpontja. F_cp=mr $\omega$ ², így azt kell még belátnunk, hogy ha OA=r₁, OB=r₂,OC=r₃, akkor m₁r₁ : m₂r₂ : m₃r₃ = F₁ : F₂ : F₃ Ezt belátni egy matematikai feladat, remélhetőleg sin-cos tételekkel menni fog!

Előzmény: [123] !X!, 2005-12-27 09:48:16

[125] nadorp

2005-12-28 16:00:33

Azt bizonyították be, hogy a p(x) polinom az x=1,2,...,p-1 helyeken osztható p-vel, azaz ezek a számok a polinom gyökei modulo (p). Viszont ha egy test feletti (p-2)-ed fokú polinomnak (p-1) darab gyöke van, akkor az csak a 0 polinom lehet. Ha ez a bizonyítás nem tetszett, akkor itt egy másik.

Legyen x egy p-nél kisebb pozitív egész és tekintsük a x,2x,3x,...,(p-1)x számokat. Ezek a számok nem oszthatók p-vel és bármely kettő különböző maradékot ad p-vel osztva. Ezért van pontosan egy olyan y, hogy az xy p-vel osztva 1-et ad maradékul. Ezt az y-t a x multiplikatív inverzének nevezzük modulo p. Az is látszik, hogy csak az 1 és a p-1 önmaga inverze ( ha p|x²-1, akkor p|x-1 vagy p|x+1). Az előbbiek szerint a 2,3,...p-2 számok párba állíthatók úgy, hogy a két szám szorzata 1-t ad maradékul p-vel osztva. Ebből viszont az következik, hogy

2^.3^....^.(p-2)=(p-2)! is 1-t ad maradékul mod (p).

Előzmény: [124] Iván88, 2005-12-27 18:57:36

[124] Iván88	2005-12-27 18:57:36
Hogy őszinte legyek, odáig értem, hogy x^p-l-1 osztható p-vel, de a többi nem világos. Hogy jön ide a p(x)?
Előzmény: [122] Csimby, 2005-12-24 23:46:27

[123] !X!	2005-12-27 09:48:16
A P.3833.-as feladatra senki nem tud valami okosat mondani?

[122] Csimby

2005-12-24 23:46:27

Wilson-tétel:

Biz. vázlat:

p(x)=x^p-1-1-(x-1)(x-2)...(x-(p-1))

p(x)-ben az első tag Kis-Fermat tétel szerint 1 maradékot ad p-vel osztva (ha x nem osztható p-vel), ugyanakkor az utolsó tag (a p-1 tényezős szorzat p-1 helyen is 0 maradékot ad p-vel osztva). Tehát p(x)-nek van legalább p-1 inkongruens gyöke. De p(x) foka p-2, hiszen a főtag kiesik. Ekkor a fokszámtétel szerint (Z_p test) p(x)=0-nak legfeljebb p-2 inkongruens megoldása van. Ez ellentmondás, csak az oldja fel, ha p(x) a 0 polinom, vagyis minden együtthatója, így a₀ is 0. Viszont a₀=-1-(-1)^p(p-1)! $\equiv$ 0. Ha p>2 akkor p páratlan, tehát ezt kapjuk: -1 $\equiv$ (p-1)! Ami pont az általad megfogalmazott "sejtés".

Előzmény: [121] Iván88, 2005-12-24 23:14:03

[121] Iván88

2005-12-24 23:14:03

Sziasztok! Elakadtam a B. 3859-es feladattal. Leírom hol: Az biztos, hogy a₁=1, különben két egymást követő érték azonos lesz 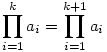$\prod_{i=1}^ka_i=\prod_{i=1}^{k+1}a_i$ , ami ellentmond a feladat állításának (1<k<n). Igaz az is, hogy a_n=n, különben biztosan lesz legalább 2 szorzat, ami n-nel osztható, és ez sem lehet. Na mármost csak olyan n-ekre teljesülhet, ahol (n-1)!=xn NEM teljesül. (x pozitív egész) Iyenek kivétel nélkül a prímszámok, és az 1, meg a 4. Amit nem sikerült tisztáznom: Igaz e, hogy mindem n prímszámra teljesül? 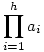az első néhány prímre kipróbáltam, és azt sejtem, hogy igen, mindegyik prímre jó, méghozzá úgy, hogy $\prod_{i=1}^ha_i$ n-nel osztva h maradékot ad (0<=h<n, egész). Igaz e? 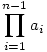Ehhez egy segédlemma: Mivel $\prod_{i=1}^{n-1}a_i$ =(n-1)!, ezért Úgy sejtem, hogy tetszőleges p prímre (p-1)!+1 p-nek egész számú többszöröse (ez ekvivalens azzal, hogy =(p-2)!-1 p-nek az egész számú többszöröse), de ezt se tudom igazolni. Talán valaki ezek után már tudja folytatni.

[120] !X!

2005-12-24 21:41:52

Sziasztok!!!

Aki megtudta csinálni a P.3833.-as feladatot, legyenszíves írja be a megoldását. Köszönöm

Boldog Karácsonyt mindenkinek!!!

[119] lorantfy	2005-12-23 14:25:36
Tükrözzük az ABM $\Delta$ -et az AB egyenesre. Itt is egy ismert tételre kell hivatkoznunk: Adott körbe írt $\Delta$ -ek közül a szabályos $\Delta$ kerülete a legnagyobb.

Előzmény: [116] lorantfy, 2005-12-22 09:37:32

[118] lorantfy	2005-12-23 10:45:33
A P pont az, ahonnan a motor húzza a kötelet. A körmozgás helyett mondhatjuk úgy is, hogy a test vizszintes irányú gyorsulása felbontható egy kötélirányú, a_cp és egy arra merőleges, a_e komponensre.
Előzmény: [117] Iván88, 2005-12-22 17:19:25

[117] Iván88	2005-12-22 17:19:25
Szia Mate! A megoldásod világos, csak azt nem látom, hogy hol van az a P pont ami körül a test körmozgást végez. (Egyébként én is a deriválásos módszerrel próbálkoztam, de semmi nem jött ki, legkevésbé a jó eredmény.)
Előzmény: [108] Mate, 2005-12-20 18:50:12

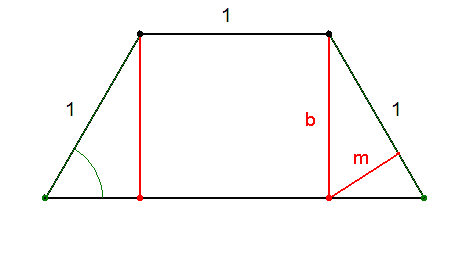
[116] lorantfy	2005-12-22 09:37:32
Hát ha erre lehet hivatkozni, akkor kész vagyunk. Én is gondoltam rá, de ez ugyanaz a szélsőérték probléma, csak ismertebb formában. Gondolod erre megadják a 4 pontot? Egy másik ötlet: Legyen a trapáz magassága b, a részháromszög átfogóhoz tartozó magassága m. Ekkor a trapéz területe: T=b+m. Egységnyi átfogójú derékszögű $\Delta$ -ben mikor max. a befogó és az átfogóhoz tartozó magasság összege?

Előzmény: [115] Mate, 2005-12-21 21:50:48

[115] Mate

2005-12-21 21:50:48

Fizikásként kontárkodom bele a feladatba. Én így oldanám meg a példát:

Keressük egy olyan trapéz alapját, melynek a másik alapja és a két szára 1 egység, úgy, hogy a trapéz területe maximális legyen.

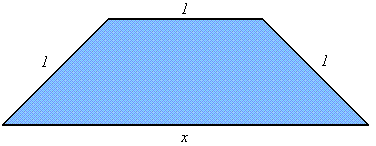
Tükrözzük a trapézt az alapjára! Ekkor visszavezetjük a problémát a következő feladatra: Melyik az az egyenlő oldalú (az egyik átlójára szimmetrikus) hatszög, amelynek területe maximális?

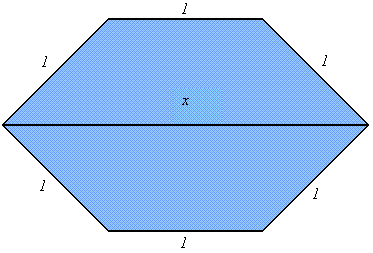
Az viszont ismeretes, hogy adott kerületű (tetszőleges) hatszögek közül a szabályosnak a legnagyobb a területe. Tehát a keresett trapézunk egy szabályos hatszög fele, így x=2.

[114] Yegreg

2005-12-21 16:29:56

Valami tiszta geometriai megoldás engem is érdekelne. (gondolom, hogy van pl. geometriai transzfomációs "hú, tényleg..." szerű megoldás :) ) Ugyanis én eddig senkiről nem tudok, aki így csinálta volna. Én megsejtettem az eredményt, és aztán teljes négyzetekkel bizonyítottam, hogy az a maximum.

Yegreg

[113] lorantfy

2005-12-21 15:28:36

Köszönöm! Még egy deriválós megoldás a B. 3857. feladatra: Egy trapéz egyik alapja és két szára egységnyi. Válasszuk meg a trapéz másik alapját úgy, hogy területe a lehető legnagyobb legyen.

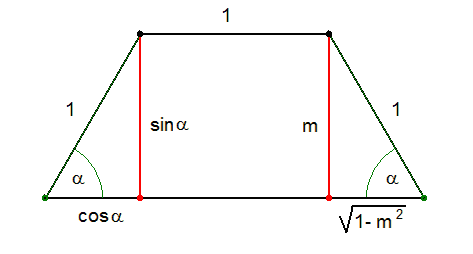
I. Legyen a változónk a trapéz alapon fekvő $\alpha$ szöge. Fejezzük ki a trapéz területét $\alpha$ segítségével.

Az alap a=1+2cos $\alpha$ a magasság m=sin $\alpha$ . A terület és $\alpha$ szerinti első deriváltja:

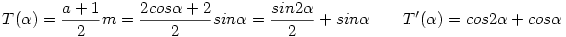
$T(\alpha)=\frac{a+1}{2}m=\frac{2cos\alpha+2}{2}sin\alpha=\frac{sin2\alpha}{2}+ sin\alpha \qquad T'(\alpha)=cos2\alpha+cos\alpha$

A maximum ott lehet, ahol a derivált 0. cos2 $\alpha$ +cos $\alpha$ =0 átalakítva: 2cos² $\alpha$ +cos $\alpha$ -1=0 egyenletet kell megoldanunk. Mivel 0< $\alpha$ <90^o várható, így cos $\alpha$ =1/2, vagyis $\alpha$ =60^o

II. Legyen a változó a trapéz magassága, ekkor a terület m-mel kifejezve és ennek első deriváltja:

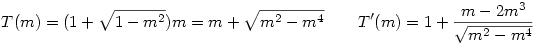
$T(m)=(1+\sqrt{1-m^2})m=m+\sqrt{m^2-m^4}\qquad T'(m)=1+\frac{m-2m^3}{\sqrt{m^2-m^4}}$

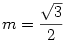Ahol a derivált 0, ott szélsőérték lehet. Ebből rendezve, m $\ne$ 0-val leosztva kapjuk a következő egyenletet: 4m²-3=0, amiből a magasságra: $m=\frac{\sqrt3}{2}$ adódik.

Mivel pont 60^o-nál, illetve 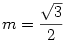$m=\frac{\sqrt3}{2}$ -nél van a maximum, gondolom van szép geometriai megoldás is. Erre sajnos még nem jöttem rá. Örülnék, ha valaki beírná!

Előzmény: [111] Mate, 2005-12-21 12:26:11

[112] Mate	2005-12-21 12:27:26
Egyébként a feladatot én javítom, és eddig mindenki a deriválós megoldást küldte be.

Már regisztráltál?
Új vendég vagy?