|
|
|
| [776] Maga Péter | 2013-03-15 10:30:56 |
 Tehát ha g konstans tagja 0, akkor g(l) n-nél kisebb fokú együtthatói pn-nel oszthatók. Legyen f=g(0)+g(1)+...+g(l-1). Mennyi ekkor g-(f-f*)?
|
| Előzmény: [775] w, 2013-03-15 10:14:24 |
|
| [775] w | 2013-03-15 10:14:24 |
 m=1, k=1: cf0,1(g*) 0 (mod p1) 0 (mod p1)
Tehát már m=2-re működik:
cf0,1(g(2)) 0 (mod p2). 0 (mod p2).
Indukcióval
cf0,1(g(k)) 0 (mod pk). 0 (mod pk).
(1)-ből kiindulva, m=2-re áttérve
cf0,1,2(g(2)) 0 (mod p1), 0 (mod p1),
így m, és "ezen belül" k szerinti indukcióval
cf0,1,...,m-1(g(m+k)) 0 (mod pk). 0 (mod pk).
Az látszik ebből, hogy a minimális  szám, melyre szám, melyre 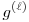 n-nél kisebb fokú együtthatói biztos pn-nel oszthatók, az n-nél kisebb fokú együtthatói biztos pn-nel oszthatók, az  =2n. =2n.
|
| Előzmény: [774] Maga Péter, 2013-03-15 00:23:33 |
|
| [774] Maga Péter | 2013-03-15 00:23:33 |
 Megpróbálom összefoglalni. Ha f olyan, hogy a konstans tagja 0, és benne a k-nál kisebb fokú együtthatók mind oszthatók pm-nel, és a pontosan k fokú együttható osztható pm-1-nel, akkor f*-ban a legfeljebb k fokú együtthatók mind oszthatók pm-nel.
Most azt bizonyítsd be, hogy ha g konstans tagja 0, akkor (rögzített n mellett) ha elég sokszor alkalmazzuk rá a *-ot, egy olyan polinomot kapunk, amelyben az n-nél kisebb fokú együtthatók pn-nel oszthatók. Tehát mondjuk legyen g(0)=g, g(1)=g*, általában g(k)=(g(k-1))*. Bizonyítsd be, hogy ha g konstans tagja 0, akkor elég nagy N-re (n előre rögzített), g(N) n-nél kisebb fokú együtthatói pn-nel oszthatók.
|
| Előzmény: [773] w, 2013-03-14 22:22:49 |
|
| [773] w | 2013-03-14 22:22:49 |
 Jelölje cfi(h) az h polinom i fokú együtthatóját.
Nyilván h=f* és i=1,2,3,...,k-1 esetén ez pm-mel osztható. Tekintsük cfk(f*)-t. A k-adfokú tagot a kisebb fokú tagok hozzák létre ( 0 mod pm), és még hozzáadódik az együtthatóhoz akp, ami ugyanezt teljesíti. cfk+1(f*) következik. Korábbi fokú tagok, ak is benne van, de ak+1p miatt semmit sem tudunk már erről (és nem is kell róla) mondani. 0 mod pm), és még hozzáadódik az együtthatóhoz akp, ami ugyanezt teljesíti. cfk+1(f*) következik. Korábbi fokú tagok, ak is benne van, de ak+1p miatt semmit sem tudunk már erről (és nem is kell róla) mondani.
Érdekes lépés. Végtelen leszállással próbáltam megközelíteni, de túlegyszerűsítettem a dolgot. Úgy látszik, itt is ez lesz.
Az f(x) polinom elég, ha n-edfokú (talán pár nulla "együtthatóval").
|
| Előzmény: [772] Maga Péter, 2013-03-14 16:08:17 |
|
| [772] Maga Péter | 2013-03-14 16:08:17 |
 Tegyük fel, hogy f(x)=aNxN+...+akxk+...+a1x, ahol a1,...,ak-1 mind oszthatók pm-nel, ak pedig nem osztható pm-nel, de osztható pm-1-gyel. Mit tudunk mondani f* kis fokú együtthatóiról a pm-nel való oszthatóságot illetően?
|
| Előzmény: [770] w, 2013-03-14 15:41:55 |
|
| [771] meowmeow | 2013-03-14 16:06:23 |
 B.4521-re első körben F1, F2, F3, M C egy körön vannak: ez trivi, kb szögszámolgatás, innét szerintem legegyszerűbb a C-re való inverzió, ekkor a két kis kör két párhuzamos egyenes lesz, a nagy kör meg ezeket érinti belülről, az érintő kör meg vele egyenlő sugarú lesz, és érinti ezeket. Innét minimális számolással (a C-n átmenő kör egyenes lesz) adódik az állítás.
|
|
|
| [769] w | 2013-03-14 15:41:18 |
 B.4520-hoz nem kell Titu-lemma, van könnyebb megoldás is. Legyen p:=(y+z)/2, q:=(z+x)/2, r:=(x+y)/2. Ha ezekkel számolunk, a közepek közötti becslések nem lesznek olyan élesek. Átírva a feladatbeli kifejezést:
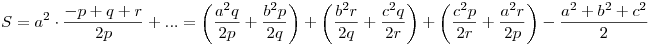
Ezt háromszor AM-GM-mel becsüljük, ekkor a, b, c háromszögoldalak mellett teljesül az összefüggés. (További vizsgálat a hivatalos megoldás szerint.)
|
|
| [768] w | 2013-03-14 15:25:38 |
 B.4515 megoldása.
Tekinthetjük a második dobást (1+2+3+4+5+6)/6=3,5-nek. Ugyanis a nyeremény várható értéke még egy dobás esetén ennek felel meg. Így elég csak az első dobással foglalkozni, illetve annak következményeivel. Feltehető még, hogy a játékos stratégikusan játszik.
Legyen az első dobás eredménye "a", a zseton ára "x". A játékos elméletileg választhat: 100a-x, vagy 350a-2x legyen a nyeresége. Akkor dob másodszor, ha 100a-x<350a-2x, azaz x/250<a.
Innen próbálgatással kapható, hogy 500<x<750. Tehát összességében a következő egyenletet elég megoldani:
100(1+2)-2x+350(3+4+5+6)-8x=0
6600=10x, x=660.
Ha a zseton ára 660 pénzegység, az üzemeltetőnek pont nulla a várható nyeresége. Tehát ennél nagyobb árú zsetonok kellenek.
-
Megjegyzés Róbert Gidának: a pénzegységet én választom meg :P (a játékot nyilván forintra találták ki) amúgy ha szigorúan vesszük igazad van :-) Azért nem így írtam a beküldött dolgozatban.
|
| Előzmény: [765] Róbert Gida, 2013-03-13 22:38:27 |
|
|
|
| [765] Róbert Gida | 2013-03-13 22:38:27 |
 Fent van már a megoldás. Bár attól elég távol van, arról sokat nem ír, hogy hogyan jött ki a megoldás. Javítóként ilyenre 0 pontot adtam volna másolás gyanúja miatt.
Egyébként az általános esetben is mindig van optimális tiszta stratégia, azaz olyan, hogy minden x-re px az nulla vagy egy. (Ezt könnyű látni).
Forintot meg ne írj, a feladat nem beszélt forintról, a megoldás sem.
|
| Előzmény: [763] w, 2013-03-13 17:06:41 |
|
| [764] w | 2013-03-13 19:28:01 |
 Jó nehéz volt a mostani A582. Van arra bizonyításom, hogy g fokszáma p-nél kisebb. Hogyan tovább? Van-e megoldásotok?
|
| Előzmény: [756] w, 2013-02-18 19:52:13 |
|
| [763] w | 2013-03-13 17:06:41 |
 Nem írtak ki a következő feladatra megoldást:
B.4515. Zseton bedobása után a játékautomata feldob egy szabályos játékkockát, majd megmutatja a dobás eredményét. Választhatunk: (1.) felvesszük a nyereményt - ami a dobott szám értékének 100-szorosa - és a játék véget ér, vagy (2.) újabb zsetont dobunk az automatába. Az utóbbi esetben a gép ismét dob, és a nyeremény a két dobott szám szorzatának a 100-szorosa. A játék legkésőbb a második dobás után véget ér. Legalább mennyi legyen a zseton ára, hogy az automata üzemeltetőjének hosszú távon nyeresége legyen?
____________________________________________________________________________________________________________
Tisztázásra vár, hogy mi a feladat helyes megoldása, hogy kell értelmezni a feltételeket. Nekem 660 jött ki, de érdekel a Ti megoldásotok is.
Igazoljuk, hogy ha a zseton ára 650 forint, a matematikus játékos számára nyereséges volna a játék.
Ezenkívül megkérdezném, mi volna, ha 1-től n-ig lehetnek a dobott számok, illetve ha más-más szorzót kap a dobott szám a kétféle körben. Mi van, ha három kör is van?
|
|
| [762] w | 2013-03-13 07:20:17 |
 B.4516. Mivel van 45 fokos szög, ezért TaFb és TbFa oldalfelező egyenesek ---> Euler-vonal.
|
|
|
|
|
| [758] Fálesz Mihály | 2013-02-26 09:08:35 |
 A nagy csendre való tekintettel,
Segítség az A.578.-hoz. Legyen f(x1,...,xk) egész együtthatós polinom, és p1,...,pk különböző prímszámok. Bizonyítsuk be, hogy
(1) Az 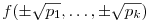 alakú számok szorzata egész szám. alakú számok szorzata egész szám.
(2) Ha 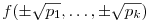 alakú számok közül valamelyik nulla, akkor mindegyik nulla. alakú számok közül valamelyik nulla, akkor mindegyik nulla.
|
| Előzmény: [756] w, 2013-02-18 19:52:13 |
|
|
| [756] w | 2013-02-18 19:52:13 |
 Az A.580 feladat az A.574 feladat továbbgondolása, és az A.574 feladatra is csak 1 helyes megoldás érkezett. Habár az internetre raktak megoldást (A.574-re), szerintem A.580-ra legfeljebb 3 jó megoldás érkezhetett. Úgy tűnik, a szükséges elméleti háttér sajnálatosan mélyen belenyúlik az egyetemi tananyagba.
A.579 is kissé szerencsétlen volt, nem tudom, ki tud(hat) a Sawayama-lemmáról.
A decemberi feladatok jók voltak, szerintem az első kettőre rá lehetett volna jönni (???), de nagyon sokat kellett volna rajtuk gondolkozni.
Az A.572 nem tűnt olyan nehéznek a statisztika alapján, az A.570 és A.578 feladattal együtt örömmel látnék rájuk megoldást.
|
| Előzmény: [755] Róbert Gida, 2013-02-18 17:01:51 |
|
| [755] Róbert Gida | 2013-02-18 17:01:51 |
 Szoros lesz az idén ez a nemhivatalos online A pontverseny. A580-ra vajon hány megoldás érkezett? Nem tűnt valami egyszerűnek a bizonyítás.
|
|




 0 (mod p1)
0 (mod p1)  szám, melyre
szám, melyre 

