|
| [16] Gubbubu | 2004-01-13 20:32:35 |
 Szia!
Valóban, úgy sejtem, a "kvázitökéletes" számok épp a kettőhatványok. A bizonyítást még nem találtam ki, ezért adtam fel a feladatot, hátha valaki gyorsabb nálam. A "segítséget" is épp azért fogalmaztam meg eléggé közvetett, rejtjelezett formában, mivel nem akartam azt mondani, hogy szerintem épp a kettőhatványok a "kvázitökéletesek", mivel fogalmam sincs, igaz-e, bár némi esély látok erre.
Jó munkát, ha még gondolkozol ezen...
Üdv: G
|
| Előzmény: [15] Sirpi, 2004-01-13 13:47:46 |
|
| [15] Sirpi | 2004-01-13 13:47:46 |
 Szia!
Nos, amit írtál igaz: valóban minden pozitív egész felírható "kvázitökéletes" számok összegeként, mert 1+2+...2k=2k+1-1, vagyis minden 2-hatvány ilyen tulajdonságú. És ezek összegeként minden szám előáll, hisz használjuk az n szám kettes számrendszerbeli alakját, ez megadja, melt 2-hatványokra van szükség az összegzéshez. Azt perpillanat nem tudom, van-e még ilyen szám, ez egy érdekes kérdésnek hangzik, de ezek is elegen vannak a számok felírásához.
S
|
| Előzmény: [14] Gubbubu, 2004-01-10 02:59:01 |
|
| [14] Gubbubu | 2004-01-10 02:59:01 |
 Halihó!
Tökéletes számnak a Püthagoreusok azokat a természetes számokat nevezték, melyek "részei" (osztói, az 1-et is beleértve, de magát a kérdéses számot nem) összege épp egyenlő volt a szóban forgó számmal.
Például a 6 tökéletes szám: 6=1+2+3.
Modern terminológiával egy szám pozitív osztóinak összegét - magát a számot is az osztók közé véve -  (n)-nel jelöljük. Például (n)-nel jelöljük. Például
 (1)=1 (1)=1
 (2)=1+2=3 (2)=1+2=3
 (6)=1+2+3+6=12=2x6 (6)=1+2+3+6=12=2x6
stb.
(hát, ez a TEX még nem megy tökéletesen...)
Egy 1-nél nagyobb n szám tehát pontosan akkor tökéletes, ha
 (n)=2n (n)=2n
Az n  (n) függvénynek sok érdekes matematikai tulajdonsága van. Például (gyengén) multiplikatív, azaz ha (a,b)=1, azaz az a, b számok relatív prímek, (n) függvénynek sok érdekes matematikai tulajdonsága van. Például (gyengén) multiplikatív, azaz ha (a,b)=1, azaz az a, b számok relatív prímek,
 (ab)= (ab)= (a) (a) (b) (b)
Viszonylag egyszerű számelméleti képlet megadja a tökéletes számokat. De engedjünk a tökéletességből egy kicsit, és:
3. feladat: Keressük meg csupán az összes "kvázitökéletes" n számot, azaz olyan számokat, melyekre
 (n)=2n-1 (n)=2n-1
.
Segítség: úgy sejtem, bármely pozitív szám felírható kvázitökéletes számok összegeként, de nem vagyok biztos.
|
|
|
|
| [11] Pach Péter Pál | 2003-12-01 21:59:52 |
 Amennyiben komolyabban foglalkoztat (valakit) ez a téma, ajánlom Surányi László: Metaaxiomatikai problémák című könyvét. A könyv első részében kimondottan a nulláról van szó.
|
| Előzmény: [8] Mate, 2003-12-01 12:15:03 |
|
| [10] Rácz Béla | 2003-12-01 13:43:49 |
 Bizonyos esetekben (pl. halmazelmélet, sőt: számítástechnika) a 0-t érdemes természetes számnak tekinteni. Az is emellett szól, hogy amit már egyszerűen meg lehet jelölni mint "pozitív egész számok", annak nem kell még egy név.
Ha azonban kissé igényesebbek vagyunk, akkor filozófiai vagy történeti jelentőséget is tulajdoníthatunk a "természetes számok" elnevezésnek. Ez elég kifejező, hiszen tényleg ez volt az első absztrakt számfogalom. Már a történelem előtti időkben tudtak egyes kultúrák számolni (2-nél tovább is ...) Az igazi mérföldkő az, amikor valaki felismeri, hogy minden számnál van eggyel nagyobb; ez már igazából elég a pozitív egész szám fogalmának tisztázásához.
A 0 azonban egészen más ügy, és csak jóval később találták fel (t.i. ismerték fel, hogy számnak lehet tekinteni), valószínűleg Indiában. Európába csak a középkorban jutott el. A helyiértékes írás ezzel szoros kapcsolatban van; valóban, a görög és a (jól ismert) római számjelölés sem helyiértékes jellegű.
(Bár definíció szintjén a görögök az 1-et sem tekintették számnak, azért nagyon jól "tudták", hogy az, ez kiviláglik pl. a tökéletes szám fogalmából: t.i. hogy az 1-et is az osztók közé kell számítani.)
Ekkorra a tört (pozitív racionális) számok már régóta ismertek voltak (már az ókori Egyiptomban is számoltak törtekkel); tehát a 0 annyira nem "természetes", hogy a törtek természetesebbek nála. (Itt persze az emberi ész járását követtem, nem pedig a szokásos iskolai rekonstrukció menetét, ami rövid és könnyen bizonyítható, nem pedig kifejező szerkezetre törekszik.)
Jogos ellenvetés persze, hogy az 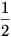 , sőt a 0 is "természetesebb", mint mondjuk a 1020 szám. Azonban fogalmi szinten ez utóbbinak a léte felfogható akkor, ha értjük, hogy minden számnál van eggyel nagyobb, míg a törtek vagy a nulla új felismerést tételeznek fel. , sőt a 0 is "természetesebb", mint mondjuk a 1020 szám. Azonban fogalmi szinten ez utóbbinak a léte felfogható akkor, ha értjük, hogy minden számnál van eggyel nagyobb, míg a törtek vagy a nulla új felismerést tételeznek fel.
Tehát szerintem mérnökies ízű az a megállapodás, hogy a 0 természetes szám; történeti és antropomorf szempontból sokkal előnyösebb, ha nem az.
Ja, természetesen a nulla páros, de - igazából megállapodás alapján - se nem pozitív, se nem negatív.
(Javítson ki nyugodtan akárki, ha valahol hülyeséget írtam.)
|
| Előzmény: [8] Mate, 2003-12-01 12:15:03 |
|
| [9] Sirpi | 2003-12-01 12:37:29 |
 A 0 egy elég érdekes állatfaj. Először is páros (a rulettet nem matematikusok készítették...), hiszen osztható 2-vel (0*2=0). Ezen kívül se nem negatív, se nem pozitív (valahol a ott van a kettő között :-) ), és arról, hogy természetes szám-e, eléggé megoszlanak a vélemények. A Magyar szabvány, meg a számelmélészek és halmazelmélészek szerint igen, de pl. az analisták szerint nem.
Erről van egy vicc is, azt a megfelelő topikba írom.
S
|
| Előzmény: [8] Mate, 2003-12-01 12:15:03 |
|
| [8] Mate | 2003-12-01 12:15:03 |
 Hello Mindenkinek! Azt jóideig nem tudtam, hogy a nulla pozitív vagy negatív, páros vagy páratlan, vagy természetes-e. Arra már rájöttem, hogy se nem páros, se nem páratlan (heszen a ruletten sem fekete, sem piros, hanem zöld), de a másik két kérdésre máig nem tudom a választ... Segítsetek!
|
|
| [7] Rácz Béla | 2003-11-25 22:46:57 |
 Jó, hogy észrevetted a párhuzamosságot a Fibonacci- és a Lucas-számok között. Ez azt jelenti, hogy Csíkvári cikkében már implicite szerepelt ez a tételecske, csak nem vettem észre akkor, hogy átültethető a Fibonacci-sorra.
Azért még jobban örülnék, ha valaki csak jól ismert dolgok felhasználásával írná le a megoldást. Ebből a szempontból szerintem könnyebb az új feltételből bizonyítani a következményt (2*).
|
| Előzmény: [6] zorbb, 2003-11-23 17:22:21 |
|
| [6] zorbb | 2003-11-23 17:22:21 |
 (Sajnos én végképp nem tudok szépen írni ezért elnézést kérek) Leírok egy megoldást a 2. feladatra: A megoldásom nagy mértékben támaszkodik a kömal 2002/1 számának a 13. és 14. oldalán kapott eredményeihez. E cikkben a Lucas sorozatokról volt szó mod n. A cikk elején leírták (amit gondolom sokan ismernek) hogy L(n)=F(n+1)+F(n-1). A 13. oldalon bebizonyítja -Csikvári Péter- a cikk írója hogy L(p) kongruens (mostantól kon-nak rövídítem) 1 (p). És a 14. oldalon pedig hogy ha p=5k+1 vagy p=5k-1 akkor L(p-1)kon 2 (p) és ha p=5n+2 vagy p=5k-2 akkor L(p+1) kon -2 (p). Most én csak azt az esetet fogom belátni amikor p=5k+1 v. p=5k-1 amásik eset bizonyítása teljesen hasonló. Tudjuk hogy L(p-1)=F(p-2)+F(p)=2F(p)-F(p-1)kon 2 (p). És L(p)=F(p-1)+F(p+1)=F(p)+2F(p-1)kon 1 (p) vagyis 2F(p)+4F(p-1)kon 2 (p) most a két kongruenciát kivonva egymásból kapjuk hogy: 5F(p-1)kon 0 (p) és mivel p>5 ezért F(p-1) osztható p-vel. Elnézést hogy ilyen hosszúra sikeredett majd legközelebb megpróbálom rövidebben. Ablonczy Dávid
|
| Előzmény: [3] Rácz Béla, 2003-11-21 02:11:01 |
|
| [5] Rácz Béla | 2003-11-22 21:20:43 |
 Azt hiszem, így a 2. feladat túlságosan technikai jellegű. Szóval módosítom:
2*. feladat:
mint 2., csak:
ha van olyan a szám, hogy a*a - 5 osztható p-vel, akkor F(p-1) osztható p-vel
különben F(p+1) osztható p-vel.
|
|
| [4] Pach Péter Pál | 2003-11-21 18:23:09 |
 Kíváncsi voltam, hogy az 1. feladatra milyen megoldást fog valaki beírni, olyat, ami oszthatóságon alapszik, vagy olyat, ami a nagyságrenden múlik (tulajdonképpen azon, hogy a négyzetszámok „kevesen” vannak). Ezek szerint az utóbbi tippem jött be. Béla, ugye 22n+1 alakú számokra gondolsz, nem pedig 22n+1 alakúakra? Először nem értettem, mert azt hittem, hogy az utóbbira, aztán leesett.
Leírok egy olyan megoldást, ami oszthatóságon alapszik. A számok:
3,3.4,3.42,…,3.4n,…
Ha a legkisebb kiválasztott tag 3.4k, akkor az összeg 22k(4l+3) alakú, ami nyilvánvalóan nem lehet négyzetszám. (Miért?) A 2. egyébként vicces példa, nem írok rá semmit, mert Béla már feladta nekünk egy matektáborban. :-)
|
| Előzmény: [2] Rácz Béla, 2003-11-21 02:01:42 |
|
| [3] Rácz Béla | 2003-11-21 02:11:01 |
 Ha már számelmélet, kitűzöm ezt a kis példát. Biztos, hogy ismert tétel, ezért mikor kijött, meglepődtem, hogy még sehol nem találkoztam vele. Szóval:
2. feladat
Legyen F(n) a Fibonacci-sor, F(0) = 0, F(1) = 1. Legyen p>5 prímszám. Bizonyítandó, hogy:
- ha p 1 vagy 4 maradékot ad 5-tel osztva, akkor F(p-1) osztható p-vel.
- ha viszont 2 vagy 3 maradékot ad, akkor F(p+1) osztható p-vel.
|
|
| [2] Rácz Béla | 2003-11-21 02:01:42 |
 (Elnézést, nem tudok szépen írni. Szóval az egyszerű egymás után írás most a hatványozást fogja jelenteni.)
Az 1. feladatra:
Simán vannak ilyen számok. Most csak a létezésüket látom be, de explicite meg is lehet adni egy ilyen halmazt, ha valaki akarja.
Szóval válasszunk sorra n2 + 1 alakú számokat a következőképpen:
Először válasszuk ki az 1-et. Majd minden lépésben egy olyan n2 + 1 alakú számot, hogy ehhez az összes előzőt hozzáadva az összeg még (n+1)2-nél kisebb legyen.
Mindezt tegyük a végtelenségig. Könnyen látható, hogy tényleg nincs a kiválasztott számok között néhány olyan, hogy összegük teljes négyzet legyen: ezek között lenne egy legnagyobb, mondjuk k2 + 1. Így az összes összeadandó összege nagyobb, mint k2, de a k megválasztása miatt kisebb, mint (k+1)2, tehát nem négyzetszám.
Azt hiszem, hogy pl. a 2(2n) + 1 alakú számok, ahol n=1, 2, ... teljesítik a feltételeket.
|
| Előzmény: [1] Sirpi, 2003-11-20 08:56:16 |
|
| [1] Sirpi | 2003-11-20 08:56:16 |
 Sziasztok!
Mivel a biliárdgolyós témában elég sok számelméleti dolog merült fel, amik igazából ott nem tisztázhatók kellő mélységben, ezért arra gondoltam, hogy itt külön lehetne őket tárgyalni.
Első észrevételem pedig az ott vázolt "párosítófüggvénnyel" kapcsolatban lenne, mégpedig, hogy igazából nem párosítófv.-re van szükségünk, mert nem kell, hogy minden szám elő is álljon függvényértékként.
És hogy álljon itt egy számelmélet feladat is, jöjjön a következő:
1. feladat:
Van-e olyan végtelen részhalmaza a pozitív egészeknek, melyből bárhogy választunk ki véges sok elemet, azok összege nem négyzetszám?
S
|
|
