| [51] Fálesz Mihály | 2013-01-28 13:56:59 |
 Ha a hiperbolikus síkot a projektív síkba (elliptikus geometriába) ágyazzuk be a Klein-modellel, akkor egy görbének látszanak.
Ha viszont a hiperbolikus síkot az inverzív síkba (gömbi geometriába) ágyazzuk be valamelyik Poincaré-modellel, akkor különböző görbének látszanak.
|
| Előzmény: [47] Vonka Vilmos Úr, 2013-01-28 12:23:00 |
|
|
| [49] Vonka Vilmos Úr | 2013-01-28 13:40:19 |
 A húrnégyszögek tételének ez a hiperbolikus általánosa igen szép (és úgy látom, elég friss) eredmény (én legalábbis 2009-es és 2011-es hivatkozásokat találtam rá).
Tisztázni kell azonban előtte, hogy mit is értünk a hiperbolikus síkon húrnégyszögön. Ahhoz, hogy ilyen tételt fogalmazhassunk meg, a húrnégyszögeket a következő módon érdemes definiálni: olyan négyszög, amelynek csúcsai egy körre, horociklusra, vagy egy ekvidisztáns görbe egy ágára illeszkednek.
|
| Előzmény: [48] marcius8, 2013-01-28 13:29:25 |
|
| [48] marcius8 | 2013-01-28 13:29:25 |
 Sokan hivatkoznak a CK-modellre, ami nem baj. De szerintem az igazi nem-euklideszi geometria az, ha a tételeket közvetlenül, nem pedig modell alapján bizonyítjuk, azaz mintha nem-euklideszi síkra születtünk volna.
Más: Korábbi hozzászóló kérdezte a húrnégyszögek tételét: tetszőleges geometriában egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének az össszege egyenleő a négyszög másik két szemközti szögének összegével. Euklideszi geometriában ennél több is igaz: Egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének az összege 180° és a négyszög másik két szemközti szögének az összege 180°. Ennek bizonyítását nem írom ide, de ha az említett hozzászóló kéri, elküldöm e-mail-ben a tétel bizonyítását.
Bertalan Zoltán (marcius8)
|
|
|
|
| [45] Fálesz Mihály | 2013-01-28 12:10:16 |
 Nekem azért fenntartásaim vannak ezzel.
Arról van ugye szó, hogy az egyenes két oldalán két, állandó görbületű görbét (távolsággörbe, hiperciklus stb.) alkotnak azok a pontok, amik az egyenestől adott távolságra vannak. Ha akarjuk, és a Klein/modellben nézzük, akkor ez a két görbe valójában egy, hasonlóan az euklieszi hiperbola két ágához. Ha viszont valamelyik Poincaré/modellben nézzük, akkor kiderül, hogy két látványosan különböző görbéről van szó. A félgöbbmodell mutatja legjobban, hogy mi az oka ennek a kettősségnek. Ezt majd lerajzolom.
* * *
De mindez csak a lényegről elterelő mellékszál, és kb. annak a kérdésnek felel meg, hogy a euklideszi háromszög köré írt kört általánosítja-e az a három párhuzamos egyenespár, ami szintén tartalmazza-e a csúcsokat.
Inkább térjünk vissza a kérdéshez: láttuk, hogy minden háromszög köré írható egy állandó görbületű, összefüggő görbe, ami lehet kör, vagy paraciklus (angolban ikább horociklusnak nevezik), vagy hiperciklus. Kérdés a topiknyitóhoz: Hogy is volt az a dolog a húrnégyszögekkel?
|
| Előzmény: [44] Vonka Vilmos Úr, 2013-01-28 11:35:06 |
|
| [44] Vonka Vilmos Úr | 2013-01-28 11:35:06 |
 A hiperbolikus háromszög mindhárom középvonala egy-egy ilyen ekvidisztáns görbe tengelye. (Ennek a ténynek a megfelelője az euklideszi síkon is igaz: mindegyik oldalegyenes és a szemköztes csúcson át azzal húzott párhuzamos, mint párhuzamos egyenespár, egy ilyen ekvidisztáns görbe.)
A bizonyítás elemi úton pl. Coxeter Non-Euclidean Geometry c. könyvében megtalálható (9.67.). Érdekes az előző hozzászólásomban említett projektív megközelítés is: például ebben a jegyzetben a 144. oldalon található meg három pontra illeszkedő, adott kúpszeletet kettősen érintő kúpszelet szerkesztése. Ha a k kúpszelet a Klein-modell határköre, akkor éppen a hiperbolikus sík adott háromszöge köré írt ekvidisztáns görbe meghatározását jelenti a feladat. A jegyzet ábráján adódó X és Y pontok ekkor pontosan a megfelelő háromszögoldalak felezőpontjai (a hiperbolikus felezőpont a modellben ugyanis éppen egy olyan pontpár belső eleme, ami konjugált a határkörre nézve és harmonikusan választja el a szakasz végpontjait). Tehát a jegyzetben olvasható szerkesztés éppen azt mutatja, hogy a középvonalak mindig egy-egy megfelelő ekvidisztáns görbe tengelyei. A negyedik ekvidisztáns görbe pedig pontosan akkor jön létre, ha az ábrán szereplő X'Y' szakasz metszi a modellkört. Mivel X'Y' éppen a felezőmerőlegesek által alkotott sugársor tartópontjának polárisa, ez pontosan akkor igaz, ha a felezőmerőlegesek közös pontja "kívül esik a hiperbolikus síkon" - tehát ha a háromszög köré nem írható kör.
|
| Előzmény: [43] jonas, 2013-01-28 10:16:28 |
|
|
| [42] Vonka Vilmos Úr | 2013-01-26 16:39:52 |
 Valóban, a hiperbolikus geometria tételeit legegyszerűbben a modellekben bizonyíthatjuk be. Például az említett Klein-modellben csak le kell fordítani a szóban forgó tételt a projektív geometria "nyelvére", és azzal a gazdag eszköztárral már jóval könnyebb a tételeket bizonyítani. (Persze ehhez azt is tudnunk kell, hogy a hiperbolikus síknak izomorfia erejéig egyetlen modellje van - ennek belátásához kell az említett kiegészítés az ideális elemekkel.) Érdekes feladat például a háromszögek oldalfelező-merőlegeseire vonatkozó említett tételt megfogalmazni a Klein-modellben és a kapott állítást projektív geometriai úton bebizonyítani.
Ha egy háromszög köré nem írható kör, abban az esetben is írható köré másféle ciklus (ez egy rögzített pontnak egy sugársor elemeire vett tükörképeinek halmaza). Tulajdonképpen ez az állítás szoros összefüggésben van azzal, hogy a felezőmerőlegesek sugársort alkotnak. Ha ugyanis ennek a sugársornak a tartópontja éppen a modellkörön van, akkor a háromszög köré ún. paraciklus ("végtelen sugarú kör") írható. Ha pedig a sugársor tartópontja a modellkörön kívül esik, a háromszög köré nem 3, hanem 4 ekvidisztáns görbe írható. (Ezek egy adott egyenestől adott távolságra levő pontok halmazai, amik a hiperbolikus síkon nem egyenesek, hanem a Klein-modellben a modellkört kettősen érintő ellipszisek.) Szintén érdekes feladat lehet (haladóknak...) a háromszög köré írható ekvidisztáns görbék szerkesztését a modellben a projektív geometria módszereivel elvégezni. A szerkesztésből ugyanis leolvasható, hogy éppen akkor van 4 megoldás, ha a felezőmerőlegesek által alkotott sugársor tartópontja a modellkörön kívül esik, egyébként a megoldások száma 3.
|
| Előzmény: [40] Fálesz Mihály, 2013-01-24 16:06:41 |
|
|
| [40] Fálesz Mihály | 2013-01-24 16:06:41 |
 Pont az ilyen megállapítások mutatják, hogy milyen nagy szükség van a modellekre. Sugársorról sokkal könnyebb beszélni akkor, ha a hiperbolikus síkot kiegészítjük ideális (végtelen távoli, sőt végtelenen túli) elemekkel.
Például a Klein-modellben a hiperbolikus síkot (teret) beágyazzuk a valós projektív síkba (térbe). A látszólag három különböző sugársor típus csak abban különbözik, hogy a közös pontjuk a modell belsejében, a modell határán vagy a modellen kívül van.
De még mindig van mit rágni a kérdésen: mi mondhatunk akkor, ha egy háromszög köré nem lehet kört írni?
|
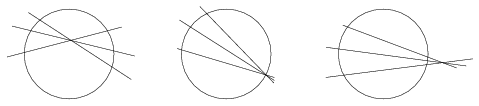 |
| Előzmény: [38] Vonka Vilmos Úr, 2013-01-24 10:57:46 |
|
| [39] Zilberbach | 2013-01-24 14:39:06 |
 Ha a definíciód szerinti alfa szög csúcsa A pont, a béta szög csúcsa B pont, akkor az egyenesen az A és B pont közötti C, harmadik "csúcspont" az elfajult háromszögbe írható kör középpontja. Indoklás: a beírható körnek érintenie kell mindhárom oldalt.
|
| Előzmény: [37] Alma, 2013-01-24 03:04:00 |
|
| [38] Vonka Vilmos Úr | 2013-01-24 10:57:46 |
 A hiperbolikus sík háromszögeinek oldalfelező merőlegeseivel kapcsolatban érdemes megjegyezni, hogy bár valóban nem mindig van közös pontjuk, az mindig teljesül, hogy sugársort alkotnak. Ez azt jelenti, hogy a következő esetek valamelyike áll fenn:
- van közös pontjuk;
- határpárhuzamosak;
- van közös merőlegesük.
|
| Előzmény: [31] marcius8, 2013-01-23 12:29:11 |
|
| [37] Alma | 2013-01-24 03:04:00 |
 Még egy apró kiegészítés: Ha a sorozatbeli háromszögek körülírható körének és beírható körének középpontjának koordinátáiból képezünk sorozatokat, akkor a beírható kör középpontjának koordinátáiból álló sorozatok konvergensek lesznek, míg a körülírható kör középpontjának (legalább) egy koordinátájának sorozata nem lesz konvergens, "a körülírható kör középpontja a végtelenben van".
Gondolkodj el azon, hogy hol van az elfajult háromszög beírható körének középpontja az én definícióm szerint!
|
| Előzmény: [36] Alma, 2013-01-23 23:52:04 |
|
| [36] Alma | 2013-01-23 23:52:04 |
 Ezeket a "maszatolásokat" meg lehet fogalmazni (legalább félig) korrektül is. Vegyünk egy olyan háromszögekből álló sorozatot, amelyeknek egyik oldala fix hosszúságú, és az azon lévő két szög ( és és  ) egyre kisebb lesz. Ha vesszük az ) egyre kisebb lesz. Ha vesszük az  -kból álló, illetve a -kból álló, illetve a  -kból álló sorozatokat, akkor legyenek ezek konvergensek, és határértékük legyen nulla. Így a háromszögekből álló sorozat olyan lesz, amely (bizonyos értelemben "konvergens") és "határértéke" egy olyan "háromszög", amelynek három csúcsa egy egyenesre esik. -kból álló sorozatokat, akkor legyenek ezek konvergensek, és határértékük legyen nulla. Így a háromszögekből álló sorozat olyan lesz, amely (bizonyos értelemben "konvergens") és "határértéke" egy olyan "háromszög", amelynek három csúcsa egy egyenesre esik.
Na most fogadjuk el a következő definíciót:
Legyen a limeszként kapott "háromszög" (melynek csúcsai egy egyenesre esnek)
a) körülírható körének sugara az a szám, amely a sorozatbeli háromszögek körülírható köreinek sugaraiból képzett sorozat határértéke,
b) beírható körének sugara az a szám, amely a sorozatbeli háromszöget beírható köreinek sugaraiból képzett sorozat határértéke.
Belátható, hogy az a)-beli határérték nem létezik, "a körülírható kör sugara végtelen". A b)-beli sorozatnak létezik határértéke, és ez 0, a beírható kör sugara 0.
Tömören: ha valahogy értelmezni akarod az elfajult háromszöged beírható és körülírható körének a sugarát, akkor a beírható kör sugara 0, a körülírható köré végtelen. Ettől még persze nem lesz jól definiált a körülírható kör, a beírható körrel szerintem nincs gond, bár én nem vagyok járatos a matematikában, ez ilyen fizikus definíció volt. :)
|
| Előzmény: [34] Zilberbach, 2013-01-23 22:03:20 |
|
|
|
| [33] Zilberbach | 2013-01-23 21:24:05 |
 Ha elfogadjuk hogy akkor tekinthető egy kör a háromszög köré írható körnek, ha mindhárom csúcsát érinti - illetve hogy egy végtelen sugarú kör egy darabja azonos lehet az egyenes egy szakaszával, akkor belátható hogy érintheti a háromszög mindhárom pontját a végtelen sugarú kör egy az adott egyenessel a háromszög három pontján egybeeső körszelete.
Elnézést kérek a fönti maszatolós elmeszüleményért, de sajnos szerintem sok hasonló akad az elfogadott geometriában és matematikában is.
|
| Előzmény: [32] Zilberbach, 2013-01-23 20:59:05 |
|
| [32] Zilberbach | 2013-01-23 20:59:05 |
 "Ennek speciális esetét érzékelhetjük az euklideszi geometriában is, amikor a háromszög csúcsai egy egyenesen vannak, - elfajult háromszög - akkor ebben az esetben sincs a háromszögnek köré írható köre." - írod.
Mint laikus érdeklődő sokszor érzem maszatolásnak a végtelenben elpattanó egyeneseket, és a még távolabbi végtelenben elpattanó egyeneseket, valamint azt is amikor egy háromszög csúcsai egy egyenesre esnek.
Akkor maszatolnék én is egy kicsit a végtelennel: ha egy háromszög csúcsai egy egyenesre esnek, akkor a köré írható (elfajult) kör sugara végtelen.
|
| Előzmény: [31] marcius8, 2013-01-23 12:29:11 |
|
| [31] marcius8 | 2013-01-23 12:29:11 |
 "FM" kérdése nagyon jó!!! A hiperbolikus síkon nem minden háromszögnek van köré írható köre. Ez adódik abból, hogy tetszőleges geometriában két adott ponttól egyenlő távol levő pontok halmaza egyenlő a két adott pont által meghatározott szakasz felezőmerőlegesével. Ebből következik, hogy tetszőleges geometriában van egy háromszögnek köré írható köre, akkor a háromszög köré írható kör körének középpontja - amely egyenlő távol van a háromszög csúcsaitól - rajta kell legyen a háromszög oldalfelező merőlegeseinek metszéspontján. Ennek a tételnek a bizonyítása a középiskolás bizonyítással megegyezzően történik. Viszont a hiperbolikus síkon a háromszög oldalfelező merőlegesei nem mindig metszik egymást, ezért nem minden háromszögnek van köré írható köre. Ennek speciális esetét érzékelhetjük az euklideszi geometriában is, amikor a háromszög csúcsai egy egyenesen vannak, - elfajult háromszög - akkor ebben az esetben sincs a háromszögnek köré írható köre.
|
|
| [30] w | 2013-01-21 21:58:40 |
 A hiperbolikus és elliptikus sík tehát valóban egy térbeli görbefelület? Hogyan értelmezhetjük akkor a rajta haladó egyeneseket stb.? Bolyai az egészet a párhuzamossági axióma újragondolásával indította, de ez hogyan vezethető le a nyeregfelületig? Le tudnátok írni alaposabban, hogy mi ezeknek a különböző változatoknak az alapja? Gondolom, enélkül értelmetlen volna a különböző tételek leírása.
|
|
| [29] Fálesz Mihály | 2013-01-21 20:25:35 |
 Ez így túl sok egyszerre. Haladjunk kisebb lépésekben. :-)
Kezdjük a háromszög köré írt körrel. Mi történik akkor, ha a háromszög oldalfelező merőlegesei nem metszik egymást?
|
| Előzmény: [28] marcius8, 2013-01-21 15:34:31 |
|
| [28] marcius8 | 2013-01-21 15:34:31 |
 Tisztelt eddigi hozzászólók!
Köszönöm az eddigi hozzászólást mindenkinek. Úgy látom, hogy a hozzászólások leginkább a hiperbolikus sík modellezéséről szólnak (nyeregfelület). Azonban a nem-euklideszi geometria másik ága a gömbi (elliptikus) geometria, az a sík ahol a gömbi geometria valósul meg, az az elliptikus sík, ennek modellezéséről eddig nem esett szó.
Amit még hiányolok, az hogy egyszerűbb középiskolás tételek, amelyek euklideszi geometriában érvényesek, hogyan szólnak nem euklideszi geometriában. 1. Például a háromszög köré írható körének középpontja egyenlő a háromszög oldalfelezőinek metszéspontjával, ez a tétel érvényes akármilyen geometriában. 2. Például euklideszi geometriában egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének összege 180°, ez csak az euklideszi geometriában érvényes, nem euklideszi geometriában egy négyszög pontosan akkor húrnégyszög, ha a négyszög két szemközti szögének összege egyenlő a négyszög másik két szemközti szögének összegével. Érdemes egyszerűbb térgeometriai tételeket is végiggondolni (például tetraéder magasságpontjára vonatkozó tétel), de aki "haladó" szinten tudja a nemeuklideszi geometriát, az egyszerűbb számolásokat is tud végezni. (Például Pitagorasz-tétel, kör kerülete, kör területe, téglatest átlója,..mind ez mindenféle geometriában, és érdemes megnézni, hogy a kapott eredmények hogyan vannak összhangban egymással...)
Mindenkinek sikeres fejtörést kívánok: Bertalan Zoltán (marcius8)
|
|
| [27] Solaris | 2013-01-19 20:18:24 |
 Nincs gond, sőt, köszönöm! Majd legközelebb a traktrix-szal kínálom meg Zilberbachot, hogy készítsen vele forgásfelületet. A traktrix forgatásával keletkező pszeudoszférán biztosan interpretálható a hiperbolikus geometria, kivéve a szinguláris pontjait. :)
A házi feladat szerintem túlzó. Ha elkészítené a modellt, akkor rájönne.
|
| Előzmény: [23] Fálesz Mihály, 2013-01-19 16:55:19 |
|
