Fórum: Projektív geometria

[1] [2] [3] [4] [5] [6]

Szeretnél hozzászólni? Jelentkezz be.

[7] sakkmath

2013-01-23 01:17:52

Ezt írod:

"(Megjegyzés: a levezetésben az osztóviszony jelölését használom. (ABC)=AB/BC, ahol A, B, C kollineáris pontok,..."

Szerintem az osztóviszony helyesen:

(ABC)=AC/CB.

Előzmény: [3] w, 2013-01-22 21:38:42

[6] m2mm

2013-01-23 00:13:56

Igen. A feladatok bizonyítása nem lesz nehéz általában, de szükséges ismeretük a későbbiekben.

Most jöjjön egy puszta alkalmazás:

3.feladat:Legyen ABCD konvex négyszög. Legyen e az A-t átmenő, BD-vel párhuzamos egyenes és f a B-n átmenő, AC-vel párhuzamos egyenes, e és f metszéspontja E. Biz. EC BD-t ugyanolyan arányban vágja el, mint ED AC-t.

A,B,C,D pontokat harmonikus pontnégyesnek nevezünk(és a,b,c,d egy ponton áthaladó egyeneseket harmonikus sugársornak), ha (ABCD)=-1(illetve (abcd)=-1). Ekkor A és C egymás harmonikus társa.

4. feladat:Bizonyítsuk be, hogy ha B,C,D pontok egy egyenesen vannak, akkor egyértelműen létezik az egyenesen harmonikus társa C-nek. (röviden harmonikus társ egyértelmű) Az is igaz, hogy ha a kettősviszonya 3 ismert és 1 ismeretlen pontnak adott, akkor az ismeretlen is ismert.

Egy újabb alkalmazás, ezt az eredményt tudni nem szükséges a továbbiakhoz:

5.feladat:Az ABC háromszögben AB=BC. ABC’, BCA’, CAB’ hasonló háromszögeket emeljük a háromszög oldalaira kifelé (AB:BC:CA=AC’:BA’:CB’=BC’:CA’:AB’). Biz. AA’, BC’, CB’ egy ponton mennek át.

Vegyük észre, hogy egy szakasz két végpontja, felezőpontja és az ideális pont(a szakaszhoz, mint egyeneshez tartozóé) harmonikus pontnégyest határoznak meg . Ez nagyon lényeges, ezért emeltem ki.

6. feladat: Ha A,B,C,D pontok ebben a sorrendben egy egyenesen vannak és harmonikus pontnégyest határoznak meg, akkor tetszőleges I pontra a síkon(leszámítva AB egyenes pontjait), pontosan akkor lesz 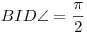$BID\angle=\frac{\pi}{2}$ , ha AIB $\angle$ =BIC $\angle$ .

[5] w	2013-01-22 22:02:20
Egy kevésbé nyilvánvaló vetítési lehetőség:

[4] w	2013-01-22 21:59:59
A 2. feladat nyilvánvalóan következik a Papposz-Steiner-tételből (1. feladat), mert a vetítésnél a P-nél lévő szögek, azaz a PA, PB, PC, PD egyenesek kettősviszonya nem változik, és ezzel az e-n és f-en lévő pontok kettősviszonya is megmarad.

[3] w	2013-01-22 21:38:42
1. feladat megoldása. A szinusztétel szerint $\frac{AC}{sinac}=\frac{AP}{sinACP<}$ , $\frac{CB}{sincb}=\frac{BP}{sinBCP<}$ . A kettőt egymással leosztva kapjuk: $(ABC):(abc)=\frac{AP}{PB}$ , hiszen ACP< és BCP< (előjeles szögek) különbsége 180 fok. (Ezt az összefüggést lehetne általánosított szögfelezőtételnek nevezni.) Ugyanitt c-t (C-t) d-vel (D-vel) helyettesítve ugyanúgy érvényben marad: $(ABD):(abd)=\frac{AP}{PB}$ . A két kapott egyenlőséget egymással leosztva: $\frac{(ABC)}{(ABD)}=\frac{(abc)}{(abd)}$ , azaz (ABCD)=(abcd). (Megjegyzés: a levezetésben az osztóviszony jelölését használom. (ABC)=AB/BC, ahol A, B, C kollineáris pontok, és (efg)=sineg/singf, ahol e, f, g egy ponton áthaladó egyenesek.)

Előzmény: [2] m2mm, 2013-01-22 13:58:23

[2] m2mm

2013-01-22 13:58:23

Versenyeken általában a projektív geo elméletét használjuk és nem egy-egy tételt kiragadva. Általában, ha proj geoval oldunk meg valamit, akkor a kettősviszonytartóságát kihasználva megfelelő vetítésekkel tudunk megoldani vele feladatot. A megfelelő vetítések alatt lehet azt érteni, hogy elküldünk pontot ideálisba/egyeneseket párhuzamossá teszünk, vagy ismert kettősviszonyú pontnégyesbe visszük. Az ismert kettősviszonyokra pedig további tételek vannak.

Így, legelőször a különböző vetítések kettősviszonyát célszerű belátni. Na de kezdjük a fogalmakkal(nem axiómákból építem fel...):

Vetítésből többféle van, vegyük először a legegyszerűbbet. Síkon adott e és f egyenes, valamint a P pont. Ha az e egyenest vetítjük f-re P-n keresztül, akkor e A pontjának a képe f és PA metszéspontja. Ekkor két dolog nincs rendben: ha P-n keresztül párhuzamost húzunk f-fel, és ez e-t metszi M-ben, akkor mi M képe? Erre vezetjük be az ideális pont elnevezést, amit a hatásvadászok néhol végtelen távoli pontnak neveznek. Minden egyenesen van egy ideális pont, egyetlen egy.

A másik kérdés, hogy minek a képe az a pont, ahol a P-n átfutó e-vel párhuzamos metszi f-et? Az e egyenes ideális pontjáé. Így a kiegészített síkon a vetítés e és f között bijekció(azért ellenőrizze mindenki, hogy tényleg más a képe különböző pontoknak).

Kettősviszonyt "elsőként" 4 pont esetén szoktunk nézni, általában kúpszeleten/egyenesen. Az A,B,C,D pontok kettősviszonya $(ABCD)=\frac{AC}{CB}:\frac{AD}{DB}$ , ahol a távolságok előjelesen értendők.

Érdemes hallani róla, hogy pl. (ABCD)=(BADC)=(DCBA).

Kettősviszonyt azonban egy ponton átmenő egyenesekre is értelmezünk, $(abcd)=\frac{\sin ac}{\sin bc}:\frac{\sin ad}{\sin db}$ , ahol a szögek ugyancsak előjelesen értendőek.

A következők lehetnek az első feladatok

1. feladat(Papposz-Steiner-tétel):Ha a,b,c,d egyenesek egy ponton mennek át és az e egyenes A,B,C,D pontokban metszi őket, akkor (ABCD)=(abcd).

2. feladat:A fentebb megadott(e->f) vetítés kettősviszonytartó.

Előzmény: [1] w, 2013-01-22 11:17:21

[1] w

2013-01-22 11:17:21

Ebben a témában írhatunk a projektív geometria fontos tételeiről és azoknak alkalmazásairól. Azért nyitom meg, mert ez a témakör az utóbbi időben igen mellőzött volt (illetve azért, mert kíváncsi vagyok, mekkora jelentősége van ezeknek a tételeknek).

A projektív geometria tételei nem igazán ismertek, ezért esetleg azzal lehetne kezdeni, hogy a továbbiakban alkalmazandó tételeket (lehetőleg elemi) bizonyítással leírjuk.

[1] [2] [3] [4] [5] [6]

Már regisztráltál?
Új vendég vagy?