Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[216] lorantfy

2004-12-05 09:56:51

Az előző egyenletrendszernek nem volt nagy sikere. Ez most jóval könnyebb:

62. feladat:

x²+xy+y²=200

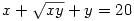
$x+ \sqrt {xy}+y=20$

[215] lorantfy	2004-11-28 16:15:29
Persze, igazad van! A (0,0,0) ránézésből megoldás, aztán még egy számhármas van.
Előzmény: [214] Lóczi Lajos, 2004-11-28 13:10:55

[214] Lóczi Lajos	2004-11-28 13:10:55
:-) A (0,0,0) is megoldás ám!
Előzmény: [213] lorantfy, 2004-11-28 11:12:05

[213] lorantfy

2004-11-28 11:12:05

Kedves Lajos!

Nekem egy valós számhármas jött ki (1,1/2,1/3) és úgy látszik nem is lehet több. Azért mertem az ujjgyakorlatok közé tenni, mert 2-3 húzással nagyon trivi formára lehet hozni.

Előzmény: [212] Lóczi Lajos, 2004-11-28 02:02:58

[212] Lóczi Lajos	2004-11-28 02:02:58
Érdekes feladat, 2 valós megoldást (számhármast) találtam, de emellett 6 komplex számhármast is, amelyek kissé bonyolult (egyváltozós) hatodfokú egyenletek megoldásaiból jönnek. Ugye nem ezekre gondoltál? :)
Előzmény: [211] lorantfy, 2004-11-27 20:59:39

[211] lorantfy

2004-11-27 20:59:39

61. feladat: Oldjátok meg az alábbi egyenletredszert:

x²-y = x²y

8y²-3z = 12y²z

18z²-x = 9z²x

[210] lorantfy

2004-11-18 09:12:44

60. feladat megoldása: Könnyű belátni, hogy

(a,b)^.[a,b]=a^.b

hiszen a lkkt-t pont úgy kapjuk, hogy a két szám szorzatából kihagyjuk a közös prímtényezőket. Ezek szorzata meg pont a lnko. Így aztán a^.b=b^.c=a^.c amiből a=b=c.

Előzmény: [208] Gubbubu, 2004-11-17 22:38:15

[209] Gubbubu	2004-11-17 22:55:33
Hát, egyelőre nemigen tudok rájönni. Sajnos, az eredeti papíromat talán egy hónapja is, hogy kidobtam, és nagyon kevés az időm, hogy újra rekonstruálni próbáljam. Na mindegy, ha valaki ki tudja valahogy javítani, csak nyugodtan, ha meg nem, hagyjuk a fenébe.
Előzmény: [207] Gubbubu, 2004-11-17 22:29:37

[208] Gubbubu

2004-11-17 22:38:15

Addig is egy új szellemes kis feladat, amiből (többek közt) ma zéháztam: 60. feladat Az a,b,c>0 egész számokra teljesül

(a,b)=(b,c)=(c,a)

és

[a,b]=[b,c]=[c,a]

(azaz lnko-ik és lkkt-ik páronként egyenlőek).

Igazoljuk, hogy a=b=c !

[207] Gubbubu	2004-11-17 22:29:37
Aha... kösz, hogy szólsz, megnézem, hogy elszámoltam-e vagy elírtam-e valamit.
Előzmény: [204] nadorp, 2004-11-10 13:31:48

[206] Gubbubu

2004-11-17 22:28:33

Igen, az a trükk, hogy a szélső tényezőket kell egymással szorozni (az elsőt a hatodikkal, a másodikat az ötödikkel, a harmadikat a negyedikkel), ekkor szinte azonos másodfokú polinomok szorzatát kapjuk, ami új változó bevezetésével szép harmadfokú egyenletté redukálható - mely utóbbit pl. "racionális gyökteszttel" lehet megoldani megfelelő n-ekre.

Köszönöm a megoldásokat.

Előzmény: [198] lorantfy, 2004-11-09 09:30:55

[205] lorantfy

2004-11-10 23:30:04

Kedves Károly!

Ügyes kis példa, de egy prímszám tábla nem árt hozzá: itt

59. feladat megoldása: A bal oldalból (p-q) kiemelhető, a 83805 minden osztója páratlan. Két prímszám különbsége csak akkor lehet páratlan, ha egyik 2.

Tehát q=2. Ezt visszaírva:

p(1+p+p³)=83827=17^.4931

Ebből p=17 és 1+p+p³ pont 4931 lesz.

Előzmény: [202] Hajba Károly, 2004-11-10 08:10:13

[204] nadorp

2004-11-10 13:31:48

Kedves Gubbubu !

Az 56. példát valahogy nem értem, mert nem igaz pld szabályos háromszögre, ui. legyen a=b=c. Ekkor szerinted

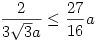$\frac{2}{3\sqrt3a}\leq\frac{27}{16}a$ , ami nyilván nem igaz minden a-ra.

Előzmény: [191] Gubbubu, 2004-10-08 09:48:03

[203] lorantfy

2004-11-10 10:01:43

Kedves Károly!

Kösz a megoldást! Valóban ennyi az egész.

Előzmény: [201] Hajba Károly, 2004-11-10 07:59:11

[202] Hajba Károly

2004-11-10 08:10:13

59. feladat:

Oldjuk meg az alábbi egyenletet, ha p és q prímek:

p+p²+p⁴-q-q²-q⁴=83.805

[201] Hajba Károly

2004-11-10 07:59:11

57. feladathoz:

m_AB+m_CD=m_Bc+m_DA=1

Azaz egy-egy pont a háromszögeket két egyenlő összterületű részre bontja, s mivel kilenc egyforma területet nem lehet két egyenlő részre bontani, így ilyen elrendezést sem fogunk tudni találni.

Előzmény: [195] lorantfy, 2004-11-09 08:45:18

[200] Hajba Károly

2004-11-09 09:48:05

Kedves KL!

Valóban. Az otthoni vázlatomból rossz sort másoltam ide. Köszi a Kemény-féle kritikát. :o)

Előzmény: [199] Kemény Legény, 2004-11-09 09:38:18

[199] Kemény Legény	2004-11-09 09:38:18
Kedves Onogur!Szerintem az A számod nem (x-3)(x-4) hanem (x-2)(x-5)=x*x-7x+10,ekkor a további folytatás jó.(Bár a megoldásokat nem ellenöriztem le..)
Előzmény: [197] Hajba Károly, 2004-11-09 08:59:01

[198] lorantfy

2004-11-09 09:30:55

Kedves Károly!

Köszönöm! Hát erről van szó. Ha megfelelően párosítjuk a szorzótényezőket az x-ek száma megegyezik, csak konstansban különböznek. Így biztos 3-ad fokú lesz belőle, ami megfelelő n-ekre szépen szorzattá alakítható.

Előzmény: [197] Hajba Károly, 2004-11-09 08:59:01

[197] Hajba Károly

2004-11-09 08:59:01

Egy kis zárójel lemaradt.

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

A=(x-3)(x-4)=x²-7x+10

(A-4)A(A+2)+16=0

A³-2A²-8A+16=0

$(A-2\bf)\rm(A-2\sqrt{2})(A+2\sqrt{2})=0$

x₁=1,246463...;x₂=1,438447...;x₃=5,753536...;x₄=5,561552...

Előzmény: [196] Hajba Károly, 2004-11-09 08:56:26

[196] Hajba Károly

2004-11-09 08:56:26

Kedves László!

Én is megoldottam, csak Lajos beelőzött. :o)

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

A=(x-3)(x-4)=x²-7x+10

(A-4)A(A+2)+16=0

A³-2A²-8A+16=0

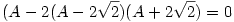
$(A-2(A-2\sqrt{2})(A+2\sqrt{2})=0$

x₁=1,246463...;x₂=1,438447...;x₃=5,753536...;x₄=5,561552...

Előzmény: [195] lorantfy, 2004-11-09 08:45:18

[195] lorantfy	2004-11-09 08:45:18
Kedves Lajos! Gratula! Szép a szorzattáalakítás, de a trükköt is megoszthatnád velünk! Felteszek még egy ábrát az 57. feladathoz hátha valakinek megtetszik!

Előzmény: [194] Lóczi Lajos, 2004-11-09 02:56:16

[194] Lóczi Lajos

2004-11-09 02:56:16

Ha "csak úgy bele a közepibe", akkor

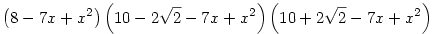$\left( 8 - 7x + x^2 \right) \left( 10 - 2 {\sqrt{2}} - 7x + x^2 \right) \left( 10 + 2 {\sqrt{2}} - 7x + x^2 \right)$ .

Gyártottam még néhány feladatot erre a kaptafára, ezek kivétel nélkül másodfokúak szorzatára bonthatók:

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+n=0, ahol n $\in$ {...,-189,-96,-35,-5,9,15,16,21,64,135,...}.

Persze a tényezők számának és az 1,2,3,4,5,6 számoknak semmi szerepük sincs, pl. (x+1)(x-2)(x+5)(x+4)(x+2)+160=0 egy másodfokú és egy harmadfokú szorzatára bomlik... stb. stb. stb.

Előzmény: [193] Gubbubu, 2004-11-08 19:37:04

[193] Gubbubu

2004-11-08 19:37:04

58. feladat (ezt én Mosóczi András egyetemi hallgatótól ismerem)

Oldjuk meg az alábbi egyenletet:

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

Nem kell megijedni ettől a jó kis hatodfokú egyenlettől. Ügyesen kell szorozgatni és alakítgatni, nem csak úgy bele a közepibe... :-))

[192] lorantfy

2004-11-07 20:00:53

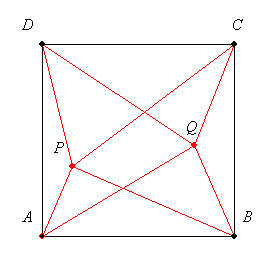
57.feladat: Egy négyzet belsejében úgy vettünk fel két pontot, hogy az ezeket a négyzet négy csúcsával összekötő szakaszok a négyzetet kilenc, közös belső pont nélküli sokszögre darabolják.

Lehet-e a kilenc sokszög területe ugyanakkora?

(Varga Tamás verseny 1998.)

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?