Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[24] Pach Péter Pál

2003-12-04 22:29:34

Igazad van, így tényleg egyszerűbb. :-) De lehet, hogy ha a kilencedikesek a szögfüggvényeket sem ismerik, akkor még a Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel sem volt dolguk. :-)

Persze át lehet írni olyan formára, ahol csak azt használjuk, hogy 0 $\le$ x², de így a CSB-egyenlőtlenségnek éppen azt a tulajdonságát veszítjük el, ami alapján könnyen észre lehet venni a megoldást.

Maga a megoldás természetesen gyors és korrekt. :-)

Előzmény: [19] Kós Géza, 2003-12-04 14:11:14

[23] Pach Péter Pál

2003-12-04 22:24:55

Kedves László!

A körülírás alapján azt hittem, hogy az 1993./3. feladatról van szó.

8. feladat

Legyen n adott pozitív egész szám. Határozzuk meg a valós számokon értelmezett

f(x)=x²ⁿ+2x^2n-1+3x^2n-2+…+(2n+1-k)x^k+…+2nx+2n+1

polinom minimumát.

Előzmény: [20] lorantfy, 2003-12-04 15:45:19

[22] Suhanc

2003-12-04 21:40:43

A teljes négyzetek:

(a-b/2)²+(c-1)²+3/4*(b-2)²<=0

Nyilván c=1, b=2 a=1

[21] lorantfy

2003-12-04 20:15:31

7. feladat:

Mely egész a, b, c, számokra igaz:

a²+b²+c²+4 $\leq$ ab+3b+2c

(1965. évi Kürschák példa alapján)

[20] lorantfy

2003-12-04 15:45:19

Az 5. feladatnál: Ha valaki persze nem akar nagyon trükközni, emelje csak négyzetre mindkét oldalt (ha a bal oldal negatív az egyenlőtlenség úgyis igaz) és alakítsa teljes négyzetté:

9x²+24xy+16y² $\leq$ 25x²+25y²

0 $\leq$ 16x²-24xy+9y²

0 $\leq$ (4x-3y)²

Láttam én már olyan Kürschák feladatot, ahol a megoldáshoz semmi más nem kellett csak ügyesen teljes négyzetekké alakítani.(Előkeresem!)

Előzmény: [17] nadorp, 2003-12-04 13:36:32

[19] Kós Géza

2003-12-04 14:11:14

Lényegében ugyanaz, de talán kicsit egyszerűbb megtalálni a megoldást Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel:

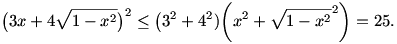
$\big(3x+4\sqrt{1-x^2}\big)^2\le\big(3^2+4^2)\bigg(x^2+\sqrt{1-x^2}^2\bigg)=25.$

Egyenlőség akkor áll, ha 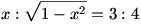$x:\sqrt{1-x^2}=3:4$ .

Azzal maximálisan egyetértek, hogy az ilyen trükköket hasznos megtanulni és begyakorolni.

Előzmény: [14] Pach Péter Pál, 2003-12-04 11:06:48

[18] lorantfy

2003-12-04 14:09:36

Kedves Nádor P.!

Nagyon gyors voltál és persze nagyon ügyes!

Most aztán megoldásod alapján rögtön általánosíthatjuk is a feladatot:

6.feladat:

Legyenek a,b,c egy derékszögű háromszög oldalai.

Bbh. 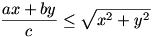$\frac{ax+by}{c}\leq \sqrt{x^2+y^2}$ .

(Más módszerrel oldjuk meg!)

Előzmény: [17] nadorp, 2003-12-04 13:36:32

[17] nadorp

2003-12-04 13:36:32

Megoldás az 5. feladatra.

Legyenek p és q pozitív egész számok, melyek értékét majd később adjuk meg. Ekkor a számtani és a négyzetes közép közötti összefüggés miatt

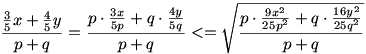
$\frac{\frac{3}{5}x+\frac{4}{5}y}{p+q}=\frac{p\cdot\frac{3x}{5p}+q\cdot\frac{4y}{5q}}{p+q}<=\sqrt{\frac{p\cdot\frac{9x^2}{25p^2}+q\cdot\frac{16y^2}{25q^2}}{p+q}}$

Ebből

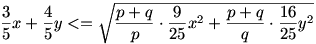
$\frac{3}{5}x+\frac{4}{5}y<=\sqrt{\frac{p+q}{p}\cdot\frac{9}{25}x^2+\frac{p+q}{q}\cdot\frac{16}{25}y^2}$

Látszik, hogy a p=9 q=16 választással épp a kívánt egynelőtlenséget kapjuk.

Előzmény: [15] lorantfy, 2003-12-04 13:01:55

[16] Hajba Károly	2003-12-04 13:25:06
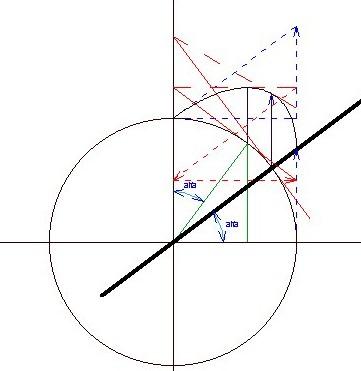
Kedves László! Én a geometria oldaláról közelítve találtam egy "csűrcsavarta" megoldást. A maximumhely X koordinátájának keresésekor nem számít, ha az egész függvényt elosztom 4-gyel. Így egy origón átmenő, 0,75 meredekségű egyenes és origó központú egység sugarú kör összegét kapjuk. Torzítsuk el képzeletben a körív minden pontját úgy, hogy az egyenes és X tengely közötti távolsággal távolítsuk az X tengelytől el. Ez a függvény képe és egyben egy ellipszis is. Szerkesszük meg a kőr és a hozzá tartozó ellipszis pontokhoz illesztett, összetartozó érintőket. Ezen érintők az Y tengelyen metszik egymást, mivel ott az eltolás 0. Az ellipszis maximumhelyéhez tartozó érintő párhuzamos az X tengellyel. Könnyen belátható, hogy e két érintő által bezárt szög $\alpha$ , így a kör ezen érintőpontját az eredeti egyenes y=x tengelyre történő tükrözött egyenessel képzett metszéspont adja. Ezt visszatéve a függvényekre, a megoldást a kör és az egyenes inverzének metszéspontja adja. 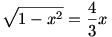$\root\of{1-x^2} = \frac43x$ Ennek eredménye éppen 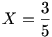$X=\frac35$ HK

Előzmény: [11] lorantfy, 2003-12-03 18:28:14

[15] lorantfy

2003-12-04 13:01:55

Na ez már igen!

Kedves Péter!

Köszönöm a megoldást!

Érdemes a "közepek" közötti összefüggéseket jól begyakorolni, mert versenyfeladatoknál és néha-néha még KÖMAL feladatokban is nagy hasznát vehetjük!

Akkor próbálkozzatok ezzel:

5.feladat Bbh. 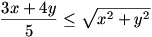$\frac{3x+4y}{5}\leq \sqrt{x^2+y^2}$

Előzmény: [14] Pach Péter Pál, 2003-12-04 11:06:48

[14] Pach Péter Pál

2003-12-04 11:06:48

Megoldás a 4. feladatra

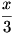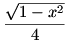Írjuk fel a számtani és a négyzetes közepek közti egyenlőtlenséget 9 darab $\frac{x}{3}$ -ra és 16 darab $\frac{\sqrt{1-x^2}}{4}$ -re:

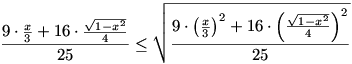
$\frac{9\cdot\frac{x}{3}+16\cdot\frac{\sqrt{1-x^2}}{4}}{25}\le\sqrt{\frac{9\cdot\left(\frac{x}{3}\right)^2+16\cdot\left(\frac{\sqrt{1-x^2}}{4}\right)^2}{25}}$

Mindkét oldalt egyszerűbb alakra hozva:

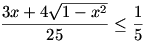
$\frac{3x+4\sqrt{1-x^2}}{25}\le\frac15$

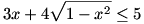
$3x+4\sqrt{1-x^2}\le5$

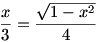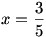Így a kifejezés maximuma 5, amit pontosan akkor vesz fel, ha $\frac{x}{3}=\frac{\sqrt{1-x^2}}{4}$ , azaz, ha $x=\frac35$ .

Előzmény: [11] lorantfy, 2003-12-03 18:28:14

[13] lorantfy

2003-12-04 00:16:58

Kedves Attila!

Szép a megoldás. Köszönet érte!

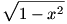$\sqrt{1-x^2}$ -ből adja magát ez a helyettesítés, de sajnos a 9-edikesek még nem tanulták matekból a szögfgv-ket. Kérdés a tankönyvírók hogy gondolták a megoldást? Hátha valakinek van még más ötlete.

Előzmény: [12] evilcman, 2003-12-03 22:47:58

[12] evilcman

2003-12-03 22:47:58

4. megoldás:

kikötés: 1>=x>=-1

ha ez az intervallum, akkor x-et helyettesíthetjük sin ( $\alpha$ ) -val

így-ha A a maximuma a függvénynek:

A=3sin ( $\alpha$ )+4cos ( $\alpha$ )

elosztjuk mindket oldalt 5-tel

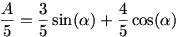
$\frac{A}{5} = \frac35\sin(\alpha) + \frac45\cos(\alpha)$

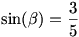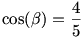
legyen $\sin(\beta) = \frac35$ ezért $\cos(\beta) = \frac45$

így addíciós képlettel:

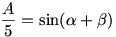
$\frac{A}{5} = \sin(\alpha+\beta)$

a sinus függvénynek a maximuma 1, vagyis az eredeti függvény maximuma 5

Innen pedig már ki lehet számolni x-et, az eredeti egyenlet egyetlen gyöke 3/5.

[11] lorantfy

2003-12-03 18:28:14

4.feladat: Keressük a maximum helyét és értékét, de semmi deriválás, kilencedikesek vagyunk!

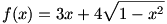
$f(x)=3x+4 \sqrt{1-x^2}$

(Sokszínű Matek 9-ből van!)

[10] Sirpi	2003-12-02 14:14:56
a^lg b=(10^lg a)^lg b=10^{lg a^.lgb}, ami szimmetrikus a-ban és b-ben, tehát C=1.
Előzmény: [9] lorantfy, 2003-12-02 14:11:11

[9] lorantfy

2003-12-02 14:11:11

Kedves Fórumosok!

Nézzetek be ide is mert kihal a téma!

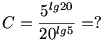
$C= \frac {5^{lg20}}{20^{lg5}}=?$

[8] Suhanc	2003-11-27 18:03:42
Igen, tényleg elírtam! Nem szerencsés:(

[7] lorantfy

2003-11-26 22:04:42

Kedves Suhanc!

Szépen elvagyunk itt ketten ebben a témában. Beírok egy megoldást - de szerintem elírtad a 4c²-et!

2. feladat megoldása: Belátjuk, hogy

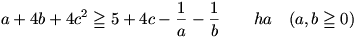
$a+4b+4c^2 \geqq 5+4c- \frac{1}{a}- \frac {1}{b}\qquad ha\quad (a,b \geqq 0)$

A 4c²-ből és a 4c-ből látszik, hogy bal oldalon egy különbség négyzete lesz, amihez kell még, hogy mindkét oldalhoz 1-et adjunk:

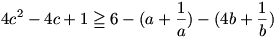
$4c^2-4c+1 \geqq 6 -(a+ \frac{1}{a})-(4b+ \frac {1}{b})$

Jobb oldalon a jól ismert egyenlőtlenség:

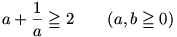
$a+ \frac{1}{a} \geqq 2 \qquad (a,b \geqq 0)$

és a második tag is ilyen lesz, ha kiemelünk 2-t:

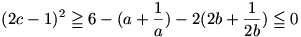
$(2c-1)^2 \geqq 6 -(a+ \frac{1}{a})- 2(2b+ \frac {1}{2b}) \leqq 0$

Előzmény: [1] Suhanc, 2003-11-23 19:04:38

[6] Suhanc

2003-11-26 18:24:56

Hahó!

Szakkörön kaptunk két érdekes feladatot, a témakört nem árulom el, elég könnyen kiderül. Az egyik tényleg villámkérdés, a másikról a szakkörvezető ennyit mondott: "aki ismeri a trükköt, annak trivi, aki még nem, annak lesz min gondolkodnia" :)

4. Bizonyítsuk be, hogy tekintve 2 ; 3; és 5 n. hatványainak összegét, van olyan két szám, melyek különbsége osztható 1237-tel. (ígérem, nemsokára megtanulom a képletszerkesztést)

5. Tekintsünk 512 egész számot! Bizonyítsuk be, hogy ki tudunk választani közülük néhányat, hogy összegük 512-vel osztható legyen! (leglább 1-et választunk ki, de akár az összeset is)

[5] lorantfy

2003-11-26 14:57:05

Kedves Suhanc!

Jól gondolod, pont a sarokház az ellenpélda a b)-nél.

A d)-nél szigorú értelemben igazad van. De ha azt mondjuk, hogy testvérek azok, akiknek legalább egyik szülője közös, akkor már nem.

Szóval tágabb értelemben egyik sem tranzitív.

Előzmény: [4] Suhanc, 2003-11-25 20:16:51

[4] Suhanc

2003-11-25 20:16:51

Kedves Lórántfy!

Ha valóban ennyire "nagy" az érdeklődés, akkor én is leírom a 3. feladatra az ötleteimet.

d)nyilván tranzitív. c) Nem tranzitív./sajnos a suli számos ellenpéldát hoz a tranzitivitásra :( /

a) ha A és B szomszédok, valamint B és C szomszédok, úgy A és C B két oldalán laknak, így nem lehetnek szomszédok (eltekintve egy olyan speciális elhelyezéstől, amelyben a 3 házat egy kör alakú utca veszi körül/

Szándékosan cseréltem fel a sorrendet, mert számomra a b) nem egyértelmű. Mi van, ha B egy sarokházban lakik. Vehetem úgy, hogy mindkét utca lakója? Ugyanis szerintem függ ettől a tranzitivitás.

Ja, az első két feladatról: az 1. Egy "Urbán: Matek+" című könyvben találtam,(egyben könyvajánlás; szerintem érdekes feladatokat rejt, egyedi megoldásokal), a második feladat pedig egy régi Arany Dani példa volt.

[3] lorantfy

2003-11-24 23:43:18

Mivel a fiatalok nem nyüzsögnek, beírom az elsőt:

1. feladat megoldása: Legyen „a” pozitív egész szám, összes pozitív osztója: p₁,p₂,p₃,...p_n.

A következő tört értékét keressük:

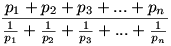
$\frac {p_1+p_2+p_3+...+p_n} {\frac {1}{p_1}+\frac {1}{p_2}+\frac {1}{p_3}+...+ \frac {1}{p_n}}$

Szorozzuk be a számlálót és nevezőt is a-val.

A nevezőben lévő összeg:

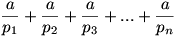
${\frac {a}{p_1}+\frac {a}{p_2}+\frac {a}{p_3}+...+ \frac {a}{p_n}}$

nem más mint „a” pozitív osztóinak összege, hiszen p_i azért osztója „a”-nak, mert létezik p_j, hogy p_ip_j=a, vagyis 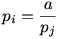$p_i=\frac {a} {p_j}$ .

Így a tört értéke: „a” .

(Persze szóban is elintézhettem volna: Ha az osztók reciprokösszegét „a”-val megszorozzuk, az osztók összegét kapjuk. Gyakoroltam kicsit a törtek beírását.)

Előzmény: [1] Suhanc, 2003-11-23 19:04:38

[2] lorantfy

2003-11-23 21:57:19

Kedves Suhanc!

Ügyes a két példa! Nem írom be a megoldást, gondolkodjon más is rajta. (Érdemes különben belenézni a TeX-be – én kimásoltam Word-be, igy folyamatosan lapozható – mert egy négyzetreemelés vagy pl. a törtek nagyon könnyen beírható és sokkal jobban mutat a képlet!)

Egy tényleg villám feladat:

3. Tranzitív egy reláció ha A $\mapsto$ B és B $\mapsto$ C $\implies$ A $\mapsto$ C

Tranzítív-e:

a) az A szomszédja B-nek

b) az A egy utcában lakik B-vel

c) az A barátja B-nek

d) az A testvére B-nek

reláció?

[1] Suhanc

2003-11-23 19:04:38

Sziasztok!

Néha túl fáradt vagyok, hogy egy-egy feladat megoldásába mélyebben elmerüljek, vagy sokáig foglalkozzam vele, és otthagyom. Gondolom, ez ismerős dolog másoknak is. Ezért szerintem jó lenne egy hely, ahova olyan feladatok kerülnek, amelyek megoldása nem igényel 10-15 percnél hosszabb elmélyülést, azonban a megoldás szép, nem darálós fajta. Kezdetnek itt van 2 -valóban ujjgyakorlatni:)-feladat:

1. Egy pozitív egész szám pozitív osztóinak összegét elosztottuk a pozitív osztók reciprokösszegével. Mennyi a hányados?

2. Ha a; b nemnegatív valós számok és c tetszőleges valós szám, bizonyítsd be, hogy:

a+4b+(4c)*(4c)>= 5+4c -1/a -1/b

(bocsi, a képletszerkesztés nem az erősségem)

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?