Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[361] Lóczi Lajos	2005-10-24 21:21:54
Pedig lehet. Segítség: cáfoljuk meg a megoldás létezését, hogy az egyenletet egy alkalmas maradékosztály felett nézzük.
Előzmény: [359] jonas, 2005-10-24 21:12:05

[360] jonas

2005-10-24 21:20:47

Ha már a pitagoraszi számhármasokról van szó, mutatok egy módszert, ahogy elő lehet állítani őket. Legyen a,b egészek.

|b+ai|=|a+bi|

ezért

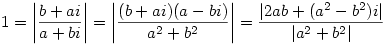
$1 = \left|\frac{b + ai}{a + bi}\right| = \left|\frac{(b + ai)(a - bi)}{a^2 + b^2}\right| = \frac{|2ab + (a^2 - b^2)i|}{|a^2 + b^2|}$

tehát a számláló és a nevező négyzete egyenlő:

(2ab)²+(a²-b²)²=(a²+b²)²

Ez persze nem bizonyítja, hogy csak ilyen alakúak lehetnek (konstans szorzótól eltekintve).

Előzmény: [358] nadorp, 2005-10-24 10:11:01

[359] jonas

2005-10-24 21:12:05

Átrendezve x⁴+y⁵=1728.

Ez érdekes egyenlet: nem tudom modulusokkal megcáfolni, de megoldást sem találtam rá (próbálgatással). Kis megoldás úgy tűnik nincs egyikre sem.

Előzmény: [353] Lóczi Lajos, 2005-10-23 17:10:39

[358] nadorp

2005-10-24 10:11:01

Itt egy érdekes adalék az eredeti problémához.

Legyenek a,b,c pitagoraszi számhármasok, azaz a²+b²=c². Ekkor

(ab)⁴+(ac)⁴+(bc)⁴=a⁴b⁴+c⁴(a⁴+b⁴)=a⁴b⁴+c⁴((a²+b²)²-2a²b²)=a⁴b⁴-2a²b²c⁴+c⁸=(c⁴-a²b²)²

Tehát a x⁴+y⁴+z⁴=t² egyenletnek végtelen sok megoldása van, ellentétben az x⁴+y⁴=t² egyenlettel,aminek egy sincs.

[357] Lóczi Lajos	2005-10-23 20:48:12
Igen, direkt szerepeltettem olyan számokat, amelyek utalnak taxicab-number-ekre, de ezt csak szándékos megtévesztésnek szántam :-), szerintem köbszámokhoz az egésznek nincs sok köze.
Előzmény: [355] Káli gúla, 2005-10-23 20:01:59

[356] Lóczi Lajos	2005-10-23 20:42:22
Természetesen próbálgattam. (A nemlineáris diofantoszi egyenletek elmélete tele van ad hoc módszerekkel, és szerintem a legnehezebb matematikák közé tartozik. Elképzelhető persze, hogy az algebrai görbék vagy varietások elméletével lehetne valamit mondani általában, de ehhez nem konyítok, messze meghaladja a képességeimet.)
Előzmény: [354] Csimby, 2005-10-23 19:49:34

[355] Káli gúla	2005-10-23 20:01:59
Érdekes szám ez, főleg így rendszám alakba normálva :) A problémás modulus köbe többféleképp írható fel három pozitív köbszám összegeként?
Előzmény: [353] Lóczi Lajos, 2005-10-23 17:10:39

[354] Csimby	2005-10-23 19:49:34
A 13 honnan jött? Elkezdtél próbálgatni vagy van valami okosabb módszer?
Előzmény: [352] Lóczi Lajos, 2005-10-23 16:43:09

[353] Lóczi Lajos

2005-10-23 17:10:39

Akkor én is generáltam egy egyenletet, ami megoldandó az egészek körében:

x⁴+y⁵+1=10³+9³.

[352] Lóczi Lajos

2005-10-23 16:43:09

Nem a kicsiség számít, hanem a maradékosztályok :)

Az egyenletnek nincs egész megoldása, ugyanis nézzünk mindent modulo 13:

egy negyedik hatvány 13-mal maradékosan osztva négyféle maradékot adhat, nevezetesen {0,1,3,9} valamelyikét,

egy harmadik hatvány 13-mal maradékosan osztva ötféle maradékot adhat: {0,1,5,8,12} valamelyikét,

viszont 19¹⁹ maradékosan osztva 13-mal 7-et ad.

És a 7 nem áll elő két olyan szám összegeként, amelyben az első tag az első halmazból, a második a másodikból van véve.

Előzmény: [351] Káli gúla, 2005-10-23 16:20:51

[351] Káli gúla	2005-10-23 16:20:51
75. feladat. Van-e egész számokból álló megoldása az x⁴+y³=19¹⁹ egyenletnek? (Valamivel kisebb a jobb oldal, mint az előző feladatban:)

[350] jonas	2005-10-23 15:29:27
Izé, ezt zárójelezni kéne, vagyis 2682440⁴+15365639⁴+18796760⁴= (-18796760)⁴+2682440⁴+15365639⁴= (-15365639)⁴+2682440⁴+18796760⁴= (-18796760)⁴+(-15365639)⁴+2682440⁴= (-2682440)⁴+15365639⁴+18796760⁴= (-18796760)⁴+(-2682440)⁴+15365639⁴= (-15365639)⁴+(-2682440)⁴+18796760⁴= (-18796760)⁴+(-15365639)⁴+(-2682440)⁴= 2061567⁴
Előzmény: [349] jonas, 2005-10-23 15:24:41

[349] jonas

2005-10-23 15:24:41

Még néhány megoldást az első alapján könnyű találni, hiszen

2682440⁴+15365639⁴+18796760⁴= -18796760⁴+2682440⁴+15365639⁴= -15365639⁴+2682440⁴+18796760⁴= -18796760⁴+-15365639⁴+2682440⁴= -2682440⁴+15365639⁴+18796760⁴= -18796760⁴+-2682440⁴+15365639⁴= -15365639⁴+-2682440⁴+18796760⁴= -18796760⁴+-15365639⁴+-2682440⁴= 20615673⁴

Előzmény: [348] Lóczi Lajos, 2005-10-23 13:56:18

[348] Lóczi Lajos	2005-10-23 13:56:18
Egy megoldást tehát találtunk, de ezzel nem szabad megelégedni. Most megkérdezem a kitűzőt, hogy árulja el az ÖSSZES TÖBBI megoldását az egyenletének, vagy mutassa meg, hogy nincs más :-)

[347] lorantfy

2005-10-23 13:54:48

Kedves Lajos!

Gratulálok! Erről van szó. A Fermat sejtés bizonyításakor komoly problémát jelentettek az Euler sejtést cáfoló számítógépes megoldások. Ezért ezeket meg lehet találni az interneten, vagy pl. Simon Signh: A nagy FERMAT sejtés c. könyvében.

2682440⁴+15365639⁴+18796760⁴=20615673⁴

Előzmény: [345] Lóczi Lajos, 2005-10-23 13:36:55

[346] Lóczi Lajos

2005-10-23 13:46:50

Á, némi internetes keresgélés után rátaláltam:

2682440⁴+15365639⁴+18796760⁴=20615673⁴

[345] Lóczi Lajos

2005-10-23 13:36:55

Euler azt sejtette (miután már tudták, hogy az x³+y³=z³ egyenletnek csak triviális megoldásai vannak a természetes számok körében), hogy az analóg x⁴+y⁴+z⁴=w⁴ egyenletnek is csak triviális megoldásai vannak. Azonban a számítógépes korszakban kiderült, hogy tévedett, mert

95800⁴+217519⁴+414560⁴=422481⁴.

[344] Lóczi Lajos	2005-10-23 13:26:50
Azt sejtem, hogy csak akkor van megoldás, ha két szám 0, a harmadik pedig a megadott (vagy az ellentettje), de a Fermat egyenleten kívüli nevezetes, ehhez hasonló egyenlet nem jut eszembe.
Előzmény: [343] lorantfy, 2005-10-23 11:15:27

[343] lorantfy	2005-10-23 11:15:27
Bocsánat Lajos! Ez a gyanútlan megoldó átverése. Nagyon nehéz, de lehet rá megoldást találni. Úgy kell elindulni, hogy elgondolkodsz milyen híres egyenlet jut róla eszedbe!
Előzmény: [342] Lóczi Lajos, 2005-10-22 23:51:25

[342] Lóczi Lajos	2005-10-22 23:51:25
Nekem ez nehéznek tűnik, a jobb oldali 4. hatvány értéke túl nagy. Hogy lehet benne elindulni?
Előzmény: [341] lorantfy, 2005-10-21 23:20:31

[341] lorantfy

2005-10-21 23:20:31

Úgy látszik mások nem járnak erre, vagy csak nincs kedvük beírni a megoldást.

Legyen egy kicsit nehezebb: 74. feladat: x<y<z egész számok, oldjuk meg az egyenletet!

x⁴+y⁴+z⁴=20615673⁴

Előzmény: [340] jonas, 2005-10-15 15:26:46

[340] jonas	2005-10-15 15:26:46
Azt is mondhatod, de a három is logikus, ha ismered a pontos feltételt a prímtényezőkkel.
Előzmény: [337] Sirpi, 2005-10-14 11:11:53

[339] Sirpi	2005-10-14 13:26:43
Na, ennek már több megoldása van. Pont annyival, mint ahányan mi vagyunk tesvérek :-) (ha csak a lényegesen kül. megoldásokat tekintjük).
Előzmény: [338] nadorp, 2005-10-14 11:40:52

[338] nadorp	2005-10-14 11:40:52
Szerintem egy dologról beszélünk, pld tekintsük a b) változatot: x²+y²=1989
Előzmény: [337] Sirpi, 2005-10-14 11:11:53

[337] Sirpi	2005-10-14 11:11:53
Eredetileg is sejtettem, csak nem állt össze a kép. Nem lenne helyesebb amúgy, ha azt mondanám, hogy 9-en vagyunk testvérek? :-) / már ha arra gondolok, amire Te /
Előzmény: [336] nadorp, 2005-10-14 11:06:52

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?