Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[766] Hajba Károly

2012-09-22 15:29:49

Ez működik más számokkal is? S ha igen, miért?

:o)

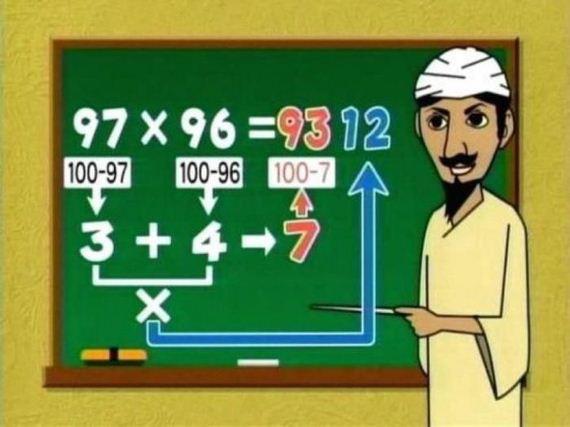[765] lorantfy

2012-08-26 21:17:35

USA versenyfeladat volt. Az orosz Duma-ra volt kiírva, aztán átfogalmazva javasoltam is B-be, persze nem a magyar parlamentre igazítva.

Tegyük fel, hogy az orosz parlamentnek 1000 tagja van és minden tag ad egy pofont pontosan egy másik tagnak. Bizonyítsuk be, hogy egy képviselő alakíthat a parlamentben egy olyan 334 tagú bizottságot amelynek egyik tagja sem adott pofont egy másik tagnak! (USA, Matematikai Tehetségkutató Verseny)

Egy internetes klubnak pontosan 1000 tagja van. Tegyük fel, hogy minden tag küld egy e-mailt pontosan egy másik tagnak. Bizonyítsuk be, hogy a tagok közül kiválaszthatunk egy olyan 334 tagú csoportot, amelynek egyik tagja sem küldött e-mailt egy másik tagnak!

Előzmény: [763] Róbert Gida, 2012-08-25 13:40:18

[764] jonas	2012-08-25 13:50:57
Ez a feladat tetszik.
Előzmény: [763] Róbert Gida, 2012-08-25 13:40:18

[763] Róbert Gida	2012-08-25 13:40:18
A 386 fős Parlamentben mindenki pontosan 1 képviselőtársát pofozta fel. Bizonyítsuk be, hogy fel lehet állítani egy 129 fős bizottságot úgy, hogy tagjai közül senki sem pofozott fel másik tagot! Továbbá lássuk be, hogy a korlát éles, azaz 130 fős ilyen bizottság nem mindig létezik.

[762] juantheron

2012-07-24 11:35:28

If x³(x+1)=(x+k)(x+2k) and 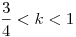$\frac{3}{4}<k<1$ ,

Then Find

(i) Number of Real Roots.

(ii) Greatest Real Root.

(iii) Least Real Root.

[761] Róbert Gida	2012-06-13 17:16:00
$\frac{D(4,5)*D(3,2)}{D(7,7)}=\frac{5675}{16213}$ a valószínűség, ahol D(i,j)-re lásd: http://oeis.org/A008288
Előzmény: [756] N.Hai, 2012-06-10 23:56:29

[760] jonas	2012-06-12 18:34:35
Úgy tűnik, hogy a pontos válasz 17025/48639 $\approx$ 0.35, ami jóval kevesebb, mint amit én becsültem.
Előzmény: [756] N.Hai, 2012-06-10 23:56:29

[759] jonas	2012-06-12 18:25:33
Hmm, a becslés nehéz. Én mondjuk 1/2-et mondok becslésnek.
Előzmény: [756] N.Hai, 2012-06-10 23:56:29

[758] Tóbi	2012-06-12 11:39:20
35%-ot tippelek.
Előzmény: [756] N.Hai, 2012-06-10 23:56:29

[757] Róbert Gida	2012-06-11 22:42:26
$\frac {\sqrt 6}{2}$
Előzmény: [755] Lóczi Lajos, 2012-06-09 21:48:27

[756] N.Hai

2012-06-10 23:56:29

Adott egy sakktábla, melynek bal alsó sarkában (A1) egy bábú áll. Ez a bábú a következőképpen mozoghat. Vagy egyet lép felfele, vagy egyet lép jobbra, vagy egyet lép átlósan a jobb felső sarokba (tehát úgy lép, mint egy király, ami folyamatosan a jobb felső sarokba tart). A király a mozgása során valamilyen úton az A1-ből a H8-ba kerül. Tegyük fel, hogy felsoroltuk az összes utat, és véletlenszerűen választunk egy útvonalat. (Tehát minden útvonal választásának az esélye ugyanakkora, függetlenül az út hosszától.) Mennyi az esélye annak, hogy egy olyan utat választottunk, amely érinti az F5 mezőt?

A feladat megoldása előtt megkérnélek titeket arra, hogy becsüljétek meg az intuíciótok alapján, hogy mekkora lehet ez a szám.

[755] Lóczi Lajos

2012-06-09 21:48:27

Egy számolás során bukkant fel az alábbi kifejezés, amely kicsit megfeküdte a gyomromat: természetesen az a cél, hogy minél egyszerűbb alakban írjuk fel. (Arra jutottam, hogy a végeredmény leírható 2 elemi művelettel és két egész számmal.)

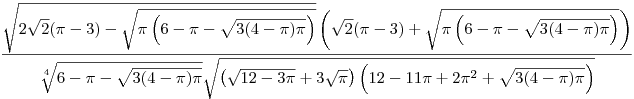
$\frac{\sqrt{2 \sqrt{2} (\pi -3)-\sqrt{\pi \left(6-\pi -\sqrt{3 (4-\pi ) \pi }\right)}} \left(\sqrt{2} (\pi -3)+\sqrt{\pi \left(6-\pi -\sqrt{3 (4-\pi ) \pi }\right)}\right)}{\root4\of{6-\pi -\sqrt{3 (4-\pi ) \pi }} \sqrt{\left(\sqrt{12-3 \pi }+3 \sqrt{\pi }\right) \left(12-11 \pi +2 \pi ^2+\sqrt{3 (4-\pi ) \pi }\right)}}$

[754] sakkmath	2012-06-06 14:38:47
Elindulhatunk így is (analízis indukcióval, a Lagrange - féle multiplikátoros módszer használatával): Először bizonyítsuk be az alábbi segédtételt.

Előzmény: [750] Lóczi Lajos, 2012-06-02 22:33:25

[753] Fálesz Mihály

2012-06-03 15:31:31

Próbálkozzunk a Hölder-egyenlőtlenség következő változatával:

Ha c_1,1,...,c_1,K,...,c_N,1,...,c_N,K nemnegatív valós számok, akkor

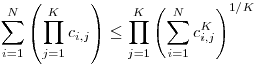
$\sum_{i=1}^N \left(\prod_{j=1}^K c_{i,j}\right) \le \prod_{j=1}^K \left(\sum_{i=1}^N c_{i,j}^K\right)^{1/K}$

(Úgy is mondhatnánk, hogy nemnegatív számokból álló táblázatban az oszlopokban vett mértani közepek átlaga legfejlebb akkora, mint a sorátlagok mértani közepe.)

Előzmény: [750] Lóczi Lajos, 2012-06-02 22:33:25

[752] juantheron	2012-06-03 13:11:05
Thanks Róbert Gida and Sakkmath.

[751] juantheron

2012-06-03 13:09:57

(1) The number of solution of sin (sin (sin x))=cos (cos (cos x))

where x $\in$ [0,2 $\pi$ ]

(2) all ordered pairs (a,b) in 5a²+5b²+5ab=5a+7b

where a,b $\in$ W

[750] Lóczi Lajos	2012-06-02 22:33:25
Akkor (ha addig nem érkezik megoldás) néhány nap múlva adhatsz számunkra tippet az elinduláshoz (pl. egy nagyon speciális esetet konkávitással beláttam, de nem látom, hogy lehet-e az általánosabb esetekben is ezzel érvelni).
Előzmény: [749] sakkmath, 2012-06-02 19:11:24

[749] sakkmath

2012-06-02 19:11:24

Kiegészítések:

1. Maradjunk a feladat eredeti szövegénél:

Az a_i-k pozitív valós számok.

Bizonyítsuk be továbbá, hogy az egyenlőtlenségben egyenlőség akkor és csak akkor áll fenn, ha a₁=a₂=...=a_n .

2. E feladat (is) inkább a "Nehezebb matematikai problémák" fejezetbe való. :( / :)

Előzmény: [748] sakkmath, 2012-06-01 15:21:23

[748] sakkmath

2012-06-01 15:21:23

Egy könnyebb feladat:

Bizonyítsuk be, hogy: ha a₁,a₂,...,a_n nemnegatív valósak, akkor

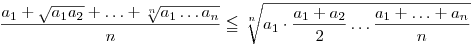
$\frac{a_1+ \sqrt{a_1a_2}+\dots + \root{n}\of{a_1\dots a_n}}{n}\leqq\root{n}\of{a_1\cdot\frac{a_1+a_2}{2}\dots\frac{a_1+\dots+a_n}{n}}$

[747] Lóczi Lajos	2012-06-01 13:49:17
:-)
Előzmény: [746] HoA, 2012-06-01 11:32:56

[746] HoA	2012-06-01 11:32:56
Akkor lehet, hogy ez sem az a tipikus "ujjgyakorlat" feladat egy középiskolások lapjának fórumán?
Előzmény: [744] Csimby, 2012-05-31 02:43:57

[745] Lóczi Lajos	2012-05-31 16:42:14
Köszönöm. (A Veljan-Korchmáros keresőkifejezésre egyébként egész sok érdekes cikket és általánosítást lehet találni, többek között a Yang S.--Wang J. kínai szerzőpáros cikkeit a 90-es évek közepéről, vagy a V. Volenec--D. Veljan--J. Pecaric hármas cikkét '98-ból.)
Előzmény: [744] Csimby, 2012-05-31 02:43:57

[744] Csimby

2012-05-31 02:43:57

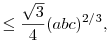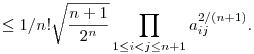a,b,c oldalú háromszög területe $\leq \frac{\sqrt{3}}{4} (abc)^{2/3},$ egyenlőség acsa, ha szabályos a háromszög. Ezt a becslést lehet általánosítani (indukcióval) n-dim szimplexre (ez az n most egy másik n mint az előző hsz-emben - konrétan 1-gyel kisebb): Ha a_ij az A_i és A_j csúcs közti él hossza, akkor a térfogat $\leq 1/n! \sqrt{\frac{n+1}{2^n}}\prod_{1\leq i < j \leq n+1} a_{ij}^{2/(n+1)}.$ Ez D. Veljan sejtése volt, a bizonyítás amit ismerek Korchmáros Gábortól származik, sajnos nem tudom linkelni, de el tudom küldeni ha érdekel (olaszul vagy németül).

Az egyenlőtlenség ebből jön ki (ez az olasz cikkben van), ha a₁,...a_n+1 poz. valósak akkor azt mondod legyen a_ij²=a_i+a_j.

De itt még kell, hogy van ilyen oldalhosszakkal szimplex. Ezt úgy lehet csinálni hogy 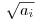$\sqrt{a_i}$ -ket felmérünk az n+1-dim tér tengelyeire és akkor ez az n+1 pont jó lesz szimplexnek.

Előzmény: [743] Lóczi Lajos, 2012-05-28 16:46:29

[743] Lóczi Lajos	2012-05-28 16:46:29
Van az egyenlőtlenség megoldására valakinek tippje? (Egyelőre csak n=3-ra van bizonyításom, de abból nem tudok továbblépni nagyobb n-ekre. Valamint tudom, hogy az állítás igaz n=4-re.)
Előzmény: [735] Csimby, 2012-05-22 20:27:55

[742] sakkmath

2012-05-27 12:37:42

I was wrong, sorry.

WolframAlpha computational knowledge engine

Előzmény: [741] Róbert Gida, 2012-05-26 22:10:59

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?