Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[847] Niels Bohr

2013-08-18 12:15:52

Sziasztok!

Beleütköztem egy hiperbola seregbe.

14x2 - 25xy + 11y2 = -6*9 = -54 19y2 - 33yz + 14z2 = -6*25 = -150 11z2 - 30xz + 19x2 = -6*64 = -384

x=17, y=20, z=25 egy megoldása.

Az ilyen típusú többismeretlenes másodfokú egyenletrendszernek hol találom a megoldás levezetését?

A segítéget előre is köszönöm.

[846] w	2013-08-18 10:21:28
Igen, így van. Kicsit érdekesebb a helyzet, de nem sokkal, ha 2013 helyére 2014-et írunk (ekkor a max. szorzat 2-vel is osztható lesz).
Előzmény: [845] aaaa, 2013-08-18 08:49:25

[845] aaaa	2013-08-18 08:49:25
3⁶⁷¹, mert jól ismert: n>4-re n<2(n-2), 4-re 2^.2=4, és 2^.2^.2<3^.3, k=k-ból indulva ez alapján cserélve az összegben a tagokat a szorzat nő, végül pedig max 2 db 2-es lehet, a többi 3-as.
Előzmény: [844] w, 2013-08-17 18:12:06

[844] w	2013-08-17 18:12:06
Néhány pozitív egész összege 2013, legfeljebb mennyi a szorzatuk?
Előzmény: [843] R.R King, 2013-08-17 08:07:45

[843] R.R King	2013-08-17 08:07:45
Szép feladat. Igaz, hogy kicsit körülményesebben, de pl. végtelen leszállással is kijön.

[842] w	2013-08-16 13:52:22
Kicsit szebben is lehet: xy\|x²-y². lnko(x,y)=d, x=da,y=db, (x,y)=1 $\implies$ d²ab\|d²(a²-b²) $\implies$ a\|b²,b\|a² $\implies$ \|a\|=\|b\|=1,\|x\|=\|y\| $\implies$ x²-y²=0=2\|xy\|z=2x²z $\implies$ x=y=0 vagy z=0 és ezek megoldások is.
Előzmény: [841] aaaa, 2013-08-16 12:45:10

[841] aaaa	2013-08-16 12:45:10
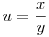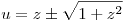x=0 ekvivalens y=0-val, ekkor z tetszőleges. Egyébként $u=\frac{x}{y}$ -ra megoldva kapjuk, hogy $u=z\pm\sqrt{1+z^2}$ , innét z=0, és \|x\|=\|y\| kell. Szóval a megoldások (0,0,n), ( $\pm$ n, $\pm$ n,0) és n tetszőleges egész.
Előzmény: [840] w, 2013-08-14 10:40:49

[840] w

2013-08-14 10:40:49

Itt egy diofantszi egyenlet:

x²-y²=2xyz.

[839] w

2013-05-23 19:25:07

Igen. Valóban ennyi, a feladat csak arról szól, hogy értsük meg :)

Írnék még három gyakorlatot.

1. Legyen n zsák pénzünk, mindegyik zsákban 1000 érmével. Tudjuk, hogy vannak hamis érmék, amik a) 1g-mal könnyebbek, b) 1g-mal eltérő tömegűek a jó érméktől. Egy zsákon belül ugyanolyan nehéz érmék vannak. Mennyi lehet az n, ha egykarú mérleggel két mérés elegendő az egyes zsákokban lévő érmék tömegének meghatározására?

2. Kétkarú mérleggel mérnénk meg egy m gramm tömegű tárgyat. Rendelkezésünkre áll 6 db 1 grammos, 6 db 7 g-os, 3 db 50 g-os, 3 db 350 g-os súly. Tudjuk, hogy m $\in$ Z_>0 és m $\le$ 1200. Meg bírjuk-e mérni a tárgyat (pontosan)?

Előzmény: [838] Micimackó, 2013-05-23 09:44:09

[838] Micimackó

2013-05-23 09:44:09

Nincs, indirekt: Legyen a a első számjegye, t a számrendszer, n a jegyei száma, x a szám, y a jegyei szorzata. Ekkor:

x $\ge$ a*t^n-1>a*(t-1)^n-1 $\ge$ y

Hiszen minden jegy maximum (t-1)

Előzmény: [836] w, 2013-05-20 18:10:34

[837] w	2013-05-20 18:40:50
Ez a link a bizonyítást is tartalmazza.
Előzmény: [835] w, 2013-05-20 18:07:42

[836] w

2013-05-20 18:10:34

Leírnék egy saját feladatot. Nagyon aranyos, Kömalban egyik pontversenybe sem illene.

Létezik-e olyan számrendszer, amelyben van olyan többjegyű szám, amely egyenlő számjegyeinek szorzatával?

[835] w	2013-05-20 18:07:42
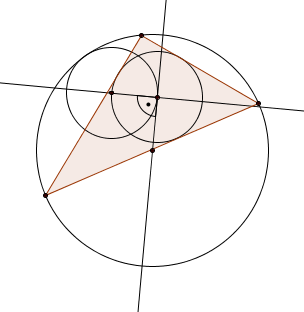
Az Euler-féle formula szerint - ami koordinátákkal igazolható - a két középpont távolságának négyzetéhez a beírt kör sugarának négyzetét hozzáadva, a kapott szám négyzetgyöke éppen a két kör sugarának különbsége, ami az érintést igazolja.
Előzmény: [834] Sinobi, 2013-05-06 23:50:51

[834] Sinobi	2013-05-06 23:50:51
Egy háromszögben a k beírt kört eltolom a beírt-körülírt körök centrálisára merőleges sugárnyi hosszú vektorral, hogy a középpontja a beírt körön legyen (lásd ábra). Bizonyítsd be, hogy az így kapott kör érinti a körülírt kört.

[833] w

2013-05-02 15:29:43

Ha valamely két szám egyenlő, akkor a kezdeti kifejezés nem értelmezhető. :-)

Nekem a nadorp-féle hozzáállás nagyon tetszik, a kifejezésről ordít az interpolációs képlet, csak felfedezni nem véltem ilyet. Amúgy az interpolációs feladatot valahol ki is tűztem a fórumon, csak válasz nem érkezett.

Előzmény: [830] Lóczi Lajos, 2013-05-02 14:53:56

[832] jonas	2013-05-02 15:11:28
Aha, értem. Szóval te most Fálesz Mihály megoldásához hasonlót szeretnél kapni.
Előzmény: [829] nadorp, 2013-05-02 14:52:23

[831] nadorp	2013-05-02 14:56:36
Így kevesebbet kellett írni. :-)
Előzmény: [830] Lóczi Lajos, 2013-05-02 14:53:56

[830] Lóczi Lajos

2013-05-02 14:53:56

>>> Tekintsük a következő p(x) polinomot. ( a $\neq$ b $\neq$ c )

És mi van, ha a=c ? :)

Előzmény: [826] nadorp, 2013-05-02 13:44:57

[829] nadorp	2013-05-02 14:52:23
a,b és c adott valós számok. A nevezőben nincs "x". p miért nem polinom?
Előzmény: [827] jonas, 2013-05-02 14:36:48

[828] Lóczi Lajos	2013-05-02 14:51:41
Mert nincs x a nevezőben.
Előzmény: [827] jonas, 2013-05-02 14:36:48

[827] jonas	2013-05-02 14:36:48
De honnan tudod, hogy p polinom (vagyis nincs nevezője)?
Előzmény: [826] nadorp, 2013-05-02 13:44:57

[826] nadorp

2013-05-02 13:44:57

Remélem, ez már jó megoldás lesz.

Tekintsük a következő p(x)polinomot. ( a $\neq$ b $\neq$ c)

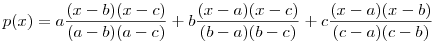
$p(x)=a\frac{(x-b)(x-c)}{(a-b)(a-c)}+b\frac{(x-a)(x-c)}{(b-a)(b-c)}+c\frac{(x-a)(x-b)}{(c-a)(c-b)}$

Látszik, hogy a p(x)=x egyenletnek az a,b és c különböző gyökei. Mivel egy másodfokú egyenletnek csak két különböző gyöke lehet, ez csak úgy lehet, ha a p(x)=x egyenlet azonosság, tehát minden x-re

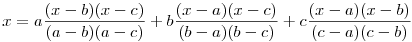
$x=a\frac{(x-b)(x-c)}{(a-b)(a-c)}+b\frac{(x-a)(x-c)}{(b-a)(b-c)}+c\frac{(x-a)(x-b)}{(c-a)(c-b)}$

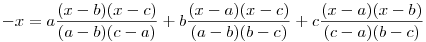
$-x=a\frac{(x-b)(x-c)}{(a-b)(c-a)}+b\frac{(x-a)(x-c)}{(a-b)(b-c)}+c\frac{(x-a)(x-b)}{(c-a)(b-c)}$

Behelyettesítve az x=a+b+c értéket

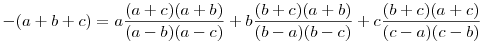
$-(a+b+c)=a\frac{(a+c)(a+b)}{(a-b)(a-c)}+b\frac{(b+c)(a+b)}{(b-a)(b-c)}+c\frac{(b+c)(a+c)}{(c-a)(c-b)}$

Előzmény: [825] nadorp, 2013-05-02 13:29:00

[825] nadorp	2013-05-02 13:29:00
Bocs, az előző megoldás hibás, még finomításra szorul
Előzmény: [824] nadorp, 2013-05-02 13:24:21

[824] nadorp

2013-05-02 13:24:21

Tekintsük a p(x)=x polinomot. Ekkor p(a)=a, p(b)=b és p(c)=c. Írjuk fel a Lagrange interpolációs képletet. Kapjuk, hogy minden x-re

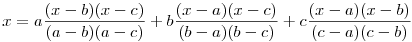
$x=a\frac{(x-b)(x-c)}{(a-b)(a-c)}+b\frac{(x-a)(x-c)}{(b-a)(b-c)}+c\frac{(x-a)(x-b)}{(c-a)(c-b)}$

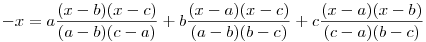
$-x=a\frac{(x-b)(x-c)}{(a-b)(c-a)}+b\frac{(x-a)(x-c)}{(a-b)(b-c)}+c\frac{(x-a)(x-b)}{(c-a)(b-c)}$

Behelyettesítve az x=a+b+c értéket

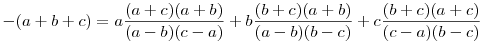
$-(a+b+c)=a\frac{(a+c)(a+b)}{(a-b)(c-a)}+b\frac{(b+c)(a+b)}{(a-b)(b-c)}+c\frac{(b+c)(a+c)}{(c-a)(b-c)}$

Előzmény: [807] w, 2013-04-29 16:36:16

[823] Fálesz Mihály

2013-04-30 23:50:11

Ennek mintájára, hozzuk egyszerűbb alakra ezt a kifejezést:

$f(x_1,\dots,x_n) = \sum_{i=1}^n \left(x_i \cdot \prod_{j\ne i}\bigg(1+\frac1{x_i-x_j}\bigg)\right)$

Ja, és ha lehet, fejben.

Előzmény: [820] Fálesz Mihály, 2013-04-30 23:02:25

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?