Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[885] w

2014-07-15 18:22:52

Legyen &tex;\displaystyle f(x)=x^{1/x}&xet;. Ekkor &tex;\displaystyle f&xet; deriváltja:

&tex;\displaystyle f'(x)=-x^{\frac 1x-2}(\ln x-1).&xet;

(Hisz láncszabállyal &tex;\displaystyle (\ln(f))'=\ln'(f)\cdot f'=\frac{f'}{f}&xet;, ahonnan

&tex;\displaystyle f'=f\cdot (\ln (f))'=x^{1/x}\cdot \left(\frac 1x \ln x\right)'=x^{1/x}\cdot \left[-\frac1{x^2}\ln x+\frac 1{x^2}\right].)&xet;

Ebből adódik, hogy &tex;\displaystyle x>e&xet; esetén &tex;\displaystyle f'(x)<0&xet;, vagyis &tex;\displaystyle f&xet; az &tex;\displaystyle [e;\infty)&xet; intervallumon monoton csökken. Tehát

&tex;\displaystyle x_i^{\frac1{x_i}}\ge (x_i+\dots+x_n)^{\frac1{x_i+\dots+x_n}},&xet;

átalakítva

&tex;\displaystyle x_i^{\frac{x_i+\dots+x_n}{x_i}}\ge x_i+\dots+x_n.&xet;

Ezt &tex;\displaystyle i=1&xet;-től &tex;\displaystyle n&xet;-ig összegezve a bizonyítandót kapjuk. (Egyenlőség pedig nem állhat fenn.)

Előzmény: [884] Cogito, 2014-07-04 21:39:42

[884] Cogito

2014-07-04 21:39:42

Remélem, nem volt még:

Legyenek &tex;\displaystyle x_1&xet;, &tex;\displaystyle x_2&xet;, . . . , &tex;\displaystyle x_n&xet; &tex;\displaystyle \ge&xet; &tex;\displaystyle e&xet;.

Bizonyítsuk be, hogy

&tex;\displaystyle x_1^{\frac{x_1 + x_2 + ... + x_n}{x_1}} + x_2^{\frac{x_2 + x_3 + ... + x_n}{x_2}} + ... + x_{n-1}^{\frac{x_{n-1} + x_n}{x_{n-1}}} + x_n \ge x_1 + 2x_2 + ... + (n - 1)x_{n-1} + nx_n&xet; .

[883] w

2014-06-24 10:26:26

Igen, tényleg, de szerintem érdekes átfogalmazás. :)

Az előbbi feladatom megoldását valaki lelőné?

Előzmény: [882] HoA, 2014-06-23 16:18:40

[882] HoA	2014-06-23 16:18:40
Egy igazi ujjgyakorlat: Igazoljuk, hogy a Geometria téma [1845] -ben kitűzött feladat egyenértékű a B 4639. KöMaL feladattal.

[881] HoA	2014-06-19 20:14:32
Ujjgyakorlatnak kicsit erősnek vélem.
Előzmény: [877] w, 2014-06-11 22:58:23

[880] w	2014-06-19 00:05:13
A Fermat-számoshoz képest a relatív prímséget igazoló utolsó lépés kicsit összetettebb (és szebb is).
Előzmény: [879] jonas, 2014-06-18 22:45:01

[879] jonas	2014-06-18 22:45:01
Ezt a feladatot ismerem az &tex;\displaystyle a = 2 &xet; esetben, és tetszik. Más &tex;\displaystyle a &xet;-ra még nem gondolkodtam el rajta, de szerintem ugyanaz a bizonyítás megy.
Előzmény: [877] w, 2014-06-11 22:58:23

[878] csábos	2014-06-12 21:41:02
Aranyos feladat, várom az elemi megoldást.
Előzmény: [876] emm, 2014-06-01 01:16:28

[877] w

2014-06-11 22:58:23

Legyen &tex;\displaystyle a>1&xet; adott egész szám, és legyen

&tex;\displaystyle a_n=\frac{a^{a^{n+1}}-1}{a^{a^n}-1}.&xet;

Bizonyítsuk be, hogy az &tex;\displaystyle (a_n)_{n=1,2,\dots}&xet; sorozat tagjai páronként relatív prímek.

[876] emm

2014-06-01 01:16:28

Ha viszont feltesszük, hogy folytonos a függvény &tex;\displaystyle [0,2e]&xet;-n, akkor már igaz. Lagrange-féle középértéktétellel: &tex;\displaystyle \exists \xi_1\in (0,e),\xi_2\in(e,2e)&xet;:

&tex;\displaystyle 0<f'(\xi_1)=\frac{f(e)-f(0)}{e-0}\implies f(e)=f(0)+ef'(\xi_1)&xet;

(1)

&tex;\displaystyle 0<f'(\xi_2)=\frac{f(2e)-f(e)}{2e-e}\implies f(2e)=f(e)+ef'(\xi_2)&xet;

(2)

&tex;\displaystyle (1)&xet; és &tex;\displaystyle (2)&xet; összevetéséből:

&tex;\displaystyle f(2e)-f(0)=e(f'(\xi_1)+f'(\xi_2))>0&xet;

Előzmény: [875] Lóczi Lajos, 2014-05-30 20:27:09

[875] Lóczi Lajos	2014-05-30 20:27:09
Igen, én is ugyanerre gondoltam.
Előzmény: [874] emm, 2014-05-30 17:00:23

[874] emm	2014-05-30 17:00:23
Ellenpélda: &tex;\displaystyle \frac{1}{e-x}&xet;, ha &tex;\displaystyle x\neq e&xet;, és &tex;\displaystyle 0&xet; különben. &tex;\displaystyle f(0)>0>f(2e)&xet;.
Előzmény: [873] Lóczi Lajos, 2014-05-29 11:07:35

[873] Lóczi Lajos	2014-05-29 11:07:35
Legyen &tex;\displaystyle f&xet; egy olyan valós függvény, amely a &tex;\displaystyle (0,2e)&xet; intervallumon van értelmezve. Azt is tudjuk, hogy &tex;\displaystyle f'(x)>0&xet; minden &tex;\displaystyle x\in (0,2e)\setminus \{e\}&xet; esetén. Bizonyítsuk be, hogy ekkor &tex;\displaystyle f(0)<f(2e)&xet;.

[872] koma	2013-12-27 18:12:58
köszönöm szépen a válaszokat:)

[871] nadorp	2013-12-27 10:17:16
Te voltál a gyorsabb :-)
Előzmény: [869] Ménkűnagy Bundáskutya, 2013-12-27 10:12:24

[870] nadorp

2013-12-27 10:16:38

A térfogat tetszőlegesen kicsi lehet. Legyen a három él x,x és 45-2x, ahol x-et később választjuk meg. Ekkor a térfogatra

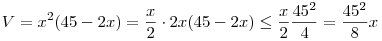
$V=x^2(45-2x)=\frac x2\cdot2x(45-2x)\leq \frac x2\frac{45^2}4=\frac{45^2}8x$

Innen látszik, hogy ha x elég kicsi, akkor a térfogat is kicsi, azaz a térfogatnak nem elfajuló téglatest esetében nincs minimuma, de tetszőlegesen közel lehet 0-hoz.

Előzmény: [868] koma, 2013-12-27 09:52:30

[869] Ménkűnagy Bundáskutya	2013-12-27 10:12:24
Ha a téglalapot elfogadod lapos téglatestnek, akkor a,45-a,0 (0 $\leq$ a $\leq$ 45) élekkel 0 a minimális térfogat. Ha nem, akkor nincs minimális térfogat: a,a,45-2a (0<a<22,5) élekkel a térfogat tetszőlegesen kicsi pozitív lehet (amint a mondjuk nagyon közel van 0-hoz).
Előzmény: [868] koma, 2013-12-27 09:52:30

[868] koma

2013-12-27 09:52:30

Sziasztok,

Egy téglatest egy csúcsából kiinduló éleinek összege 45 cm. Mekkora lehet legfeljebb a téglatest térfogata?

Ez számomra világos AM-GM-el egyszerűen oldható.

Viszont a minimális térfogatot hogyan tudnám meghatározni? Ezt nem látom jelenleg.

Kellemes ünnepeket mindenkinek!

[867] w

2013-10-30 19:44:47

Nem, én kérek bocsánatot, nem figyeltem. :-)

Így már világos.

Előzmény: [866] csábos, 2013-10-30 17:46:30

[866] csábos	2013-10-30 17:46:30
Bocsánat, ez 847-re volt válasz.
Előzmény: [857] w, 2013-10-25 18:19:41

[865] w

2013-10-29 19:29:11

Igen. Amire eredetileg gondoltam, az lényegében ezt a gondoltatmenetet csomagolja be, és egyáltalán nem induktív.

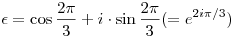Legyen $\epsilon$ harmadik komplex egységgyök, azaz $\epsilon=\cos\frac{2\pi}{3}+i\cdot\sin\frac{2\pi}3(=e^{2i\pi/3})$ . Most csak annyira lesz szükségünk, hogy létezik olyan $\epsilon$ szám, melyre $\epsilon$ ²+ $\epsilon$ +1=0.

Jelöljük f_k(n)-nel azon n-jegyű pozitív egészek számát, amelyek k maradékot adnak 3-mal osztva. Ekkor mivel nyilván $\epsilon$ ³=1, ezért $\epsilon$ ^a= $\epsilon$ ^a+3b tetszőleges a,b egész számokra. Emiatt meggondolhatjuk, hogy

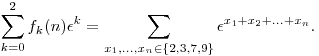
$\sum_{k=0}^2 f_k(n)\epsilon^k=\sum_{x_1,\dots,x_n\in\{2,3,7,9\}}\epsilon^{x_1+x_2+\dots+x_n}.$

Utóbbi összeg viszont nyilván nem más, mint ( $\epsilon$ ²+ $\epsilon$ ³+ $\epsilon$ ⁷+ $\epsilon$ ⁹)ⁿ, ahol $\epsilon$ ²+ $\epsilon$ ³+ $\epsilon$ ⁷+ $\epsilon$ ⁹= $\epsilon$ ²+1+ $\epsilon$ +1=1. Vagyis

f₀(n)+f₁(n) $\epsilon$ +f₂(n) $\epsilon$ ²-1=0.

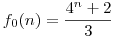Ez egy $\epsilon$ -ban másodfokú egyenlet; megoldásai: $\epsilon$ és $\epsilon$ ². Viszont x²+x+1 is olyan másodfokú polinom, melynek gyökei $\epsilon$ és $\epsilon$ ², ezért a két szóban forgó polinom igazából egymás többszöröse. Ebből adódik, hogy f₀(n)-1=f₁(n)=f₂(n), ahol viszont f₀(n)+f₁(n)+f₂(n)=4ⁿ, ezért $f_0(n)=\frac{4^n+2}{3}$ .

A fent leírt módszer általánosabb feladatok megoldására is alkalmas: például keressük meg, hány n-jegyű számnak lesznek a számjegyei 1,3,4,5,6,9 kozüliek, és 7-tel oszthatók.

Egy másik gyakorló feladat például a következő. Hány p-elemű részhalmaza van az {1,2,...,2p} halmaznak, melynek elemeinek összege p-vel osztható, ahol p páratlan prímszám?

(De ezek már tényleg nem ujjgyakorlatok.)

Előzmény: [863] Róbert Gida, 2013-10-28 17:50:03

[864] nadorp	2013-10-28 19:35:23
Elegáns
Előzmény: [863] Róbert Gida, 2013-10-28 17:50:03

[863] Róbert Gida	2013-10-28 17:50:03
Elmondom kevesebb betűvel: legyen a(n) azon n jegyűek száma melyek oszthatóak 3-mal és csak a 2,3,7,9 jegyeket tartalmazzák. Mivel 2,3,7 teljes maradékrendszer mod 3, ezért tetszőleges n-1 hosszú szám pontosan egyféleképpen egészíthető ki a 2,3,7 jegyekkel, hogy osztható legyen 3-mal, ez ad 4^n-1 lehetőséget. Ha 9-cel is ki tudjuk egészíteni, akkor ez csak úgy lehetséges, hogy már az n-1 hosszú szám is osztható volt 3-mal, azaz írhatjuk: a(n)=a(n-1)+4^n-1 és triviálisan a(1)=2, innen (mértani sorozat miatt): 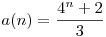$a(n)=\frac{4^n+2}{3}$ .
Előzmény: [859] nadorp, 2013-10-28 11:05:14

[862] nadorp	2013-10-28 14:34:22
Vagy [855] :-)
Előzmény: [861] nadorp, 2013-10-28 14:33:49

[861] nadorp	2013-10-28 14:33:49
Igen, elnéztem. A [255] hozzászólásra válaszoltam.
Előzmény: [860] HoA, 2013-10-28 13:30:41

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?