Fórum: Nehezebb matematikai problémák

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34]

Szeretnél hozzászólni? Jelentkezz be.

[734] kurthyg

2013-11-17 00:44:52

A következő feladatot szeretném megosztani (persze, lehet, hogy már volt, kb 15 éve olvastam KöMaL-t utoljára, még gimnáziumban).

Adott egy nxn-es négyzetrács csupa fehér négyzettel. Válasszuk ki valamelyik négyzetet, ekkor a kiválasztott négyzet, a tőle jobbra és balra, alatta és fölötte lévők feketévé változnak. És minden egyes későbbi kiválasztás ellentétes színűre változtatja a kiválasztott négyzetet és a szomszédait.

Feladat olyan utat találni, amelynek végén az összes négyzet fekete lesz. Hogyan adható meg általános megoldás?

(Pl.: 1x1-es nél triviális. 2x2-esnél minden négyzetet ki kell választani. 3x3-asnál a sarkokat és a középső négyzetet.)

A probléma általánosítása: az nxn-es négyzetrács néhány négyzete fehér, néhány négyzete fekete. Milyen út vezet csupa fekete négyzethez? Hogyan kereshető meg a megoldás? Van-e mindig megoldás?

[733] w

2013-10-25 23:07:23

A következő egy rendkívül érdekes, a pozitív valós számokra bizonyítandó egyenlőtlenség (négyzetreemelve a valósokra is érvényes marad!). Annál inkább érdekes, hogy milyen egyszerű alakú, negyedfokú egyenlőtlenség.

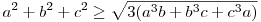
$a^2+b^2+c^2\ge\sqrt{3(a^3b+b^3c+c^3a)}$

Különösen szokatlan az egyenlőség-esete, amit mindenképpen érdemes előre megfigyelni.

(A feladat egyébként valamennyire ismert, egy idő múlva majd elárulom, hol találtam.)

[732] Sinobi	2013-10-20 01:38:34
mármint l:=-9/14*m.
Előzmény: [731] Sinobi, 2013-10-20 01:36:18

[731] Sinobi

2013-10-20 01:36:18

Bocsánat, nem ilyen alakra kell a végén hozni. Ezt még tovább kell alakítanod, hogy l:=-14/9*m, s akkor azt kapod, hogy:

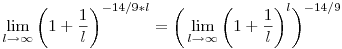
$\lim_{l\to\infty} \bigg( 1 + \frac{1}{l} \bigg) ^{-14/9*l}= \bigg( \lim_{l\to\infty} \bigg( 1 + \frac{1}{l} \bigg) ^{l} \bigg) ^{-14/9}$

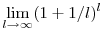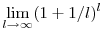Amiben még mindig ott van n a kitevőben. De azzal nem tudsz semmit se kezdeni. Igazából már Euler se tudott vele semmit kezdeni, csak feltűnt neki, hogy az olyan kifejezéseknek, melyekben n a kitevőben van, a limesze gyakran $\lim_{l\to\infty} (1+1/l)^l$ -lel és algebrai műveletekkel megadható, ezért a $\lim_{l\to\infty} (1+1/l)^l$ -et elnevezte magáról e-nek. Azóta általában az a feladat, hogy a kapott sorozatokat valahogy leredukáljuk erre a kifejezésre.

Előzmény: [730] Sinobi, 2013-10-20 01:12:11

[730] Sinobi

2013-10-20 01:12:11

Mit tanultatok már határértékből? Szerintem valami ilyesmi kell legyen:

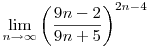
$\lim_{n\to\infty} \bigg( \frac{9n-2}{9n+5} \bigg) ^{2n-4}$

kicsit alakítjuk a limesz mögött álló formulát:

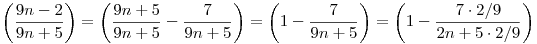
$\bigg( \frac{9n-2}{9n+5} \bigg) = \bigg( \frac{9n+5}{9n+5} - \frac{7}{9n+5} \bigg) = \bigg( 1 - \frac{7}{9n+5} \bigg) = \bigg( 1 - \frac{7 \cdot 2 / 9}{2n+5 \cdot 2/9} \bigg)$

bevezetjük az 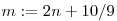$m:=2n+10/9 \frac{}{}$ változót. Ekkor a képletünk:

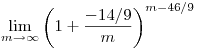
$\lim_{m\to\infty} \bigg( 1 + \frac{-14/9}{m} \bigg) ^{m-46/9}$

amit szétbontva két limesz szorzatára (majd megnézzük, hogy léteznek):

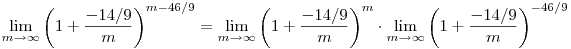
$\lim_{m\to\infty} \bigg( 1 + \frac{-14/9}{m} \bigg) ^{m-46/9} = \lim_{m\to\infty} \bigg( 1 + \frac{-14/9}{m} \bigg) ^{m} \cdot \lim_{m\to\infty} \bigg( 1 + \frac{-14/9}{m} \bigg) ^{-46/9}$

A szorzat jobb oldala 1-hez tart, a bal oldala e^-14/9-hez, tehát az eredeti is e^-14/9-hez, ami tényleg kb 0.2110.

Előzmény: [729] wartburg, 2013-10-19 23:16:25

[729] wartburg

2013-10-19 23:16:25

Kedves Topictársak, sehogy sem boldogulok az alábbi határérték feladattal: keressük az alábbi sorozat határértékét: [(9*n-2)/(9*n+5)]#(2*n-4) (a # jel hatvány jelet takarna, tehát a (2*n-4) a tört kitevője) Nem bírom a hatványt "levarázsolni" a kifejezésből, s a tört számlálóját és nevezőjét is leosztva n-nel én egyet kapnék határértéknek, ami viszont bármilyen kitevővel egy lenne. Ugyanakkor persze az Excel függvény ábrázolás szerint 0,22XXXX lenne valahol a határérték, de nekem nem jön ki ez "tudományosan". Előre is köszönöm a segítséget!

[728] nadorp	2013-10-09 15:56:10
Arra gondoltam, hogy legyen "valódi" lineáris függvény:-)
Előzmény: [727] Lóczi Lajos, 2013-10-09 14:27:42

[727] Lóczi Lajos	2013-10-09 14:27:42
Érdekes, hogy így megbonyolítottad, és nem szimplán azt írtad, hogy f(x):=0, ha x racionális.
Előzmény: [726] nadorp, 2013-10-09 12:42:30

[726] nadorp

2013-10-09 12:42:30

Ettől persze az állítás nem igaz. Legyen f(x) a következő

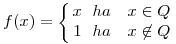
$f(x)=\left\{\matrix{x \cr 1}\right.\matrix{ha& x\in Q \cr ha& x \notin Q}$

Ekkor f(x) a racionális számok között additív, viszont tetszőleges r irracionális számra

f(r+1)=1 $\neq$ 2=f(r)+f(1)

Előzmény: [725] nadorp, 2013-10-09 09:26:56

[725] nadorp	2013-10-09 09:26:56
A hivatkozott link azt bizonyítja szerintem, hogy létezik az egyenletnek nemlineáris megoldása.
Előzmény: [723] w, 2013-10-08 14:56:22

[724] Ménkűnagy Bundáskutya

2013-10-09 08:45:17

2. (valós) Legyen A azon valós számok halmaza, melyeknek tizedestört alakja

*,*11...110s0a₁0a₂0a₃0a₄...,

vagyis valahonnan kezdve minden második jegy 0, előtte pedig néhány (esetleg 0 darab) 1-es áll (ez üres feltétel, csak így világosabb lesz). A függvény legyen A-n kívül 0, egy A-beli elemre pedig vegyük az első olyan pontot, ahonnan ez fennáll: x=*,*0s0a₁0a₂..., és s előtt három jeggyel nem 0 áll. A 0s előtt közvetlenül álló egyesek száma legyen N. Ekkor legyen f(x)=(-1)^s^.N,a₁a₂a₃....

Legyen [a,b] tetszőleges nemelfajuló intervallum, y pedig tetszőleges valós szám. Kezdjünk felírni egy valós számot. Az első sok jegyét állítsuk be úgy, hogy azok garantálják, hogy [a,b]-be esik. Ezután tegyünk le száz darab 2-est, majd |y| egész része darab 1-est, ezután lőjük be az előjelet, majd írjuk be y tizedesjegyeit 0-kal összefésülve. Az így kapott szám f-értéke y.

(komplex) Legyen f egy jó valós-valós függvény. Legyen hozzá F:C $\rightarrow$ C a következő: F(x+iy)=f(x)+if(y). Tetszőleges kicsi négyzetben, körben stb van tengelypárhuzamos téglalap, és ha F(x+iy)=u+iv a cél, akkor legyen x a téglalap valós vetületéből olyan, hogy f(x)=u, y pedig a képzetes vetületből olyan, hogy f(y)=v. Ekkor F(x+iy)=f(x)+if(y)=u+iv.

Előzmény: [722] marcius8, 2013-10-08 12:41:31

[723] w	2013-10-08 14:56:22
1. A válasz: nem igaz. Lásd itt.
Előzmény: [722] marcius8, 2013-10-08 12:41:31

[722] marcius8

2013-10-08 12:41:31

Ha valaki tud, segítsen:

1. Egy f(x) függvény additív, ha minden "p" és "q" számra teljesül, hogy f(p+q)=f(p)+f(q). Igaz-e hogy ha egy függvény a racionális számok halmazán additív, akkor ez a függvény a valós számok halmazán is additív?

2. Keressünk olyan R-->R függvényt, amely minden intervallumon minden valós számot felvesz. Illetve keressünk olyan C-->C függvényt, amely minden "négyzet alakú tartományon" (vagy "minden kör alakú tartományon") minden komplex számot felvesz.

Mindenkinek köszönöm a segítségét. Bertalan Zoltán.

[721] Zilberbach	2013-10-08 00:42:47
Pontosítok: 2 és 3 között is van egy hirtelen (föl)ugrás a függvény értékében, 3 és 4 között pedig több mint egy hirtelen (föl)ugrás.
Előzmény: [720] Zilberbach, 2013-10-07 20:38:32

[720] Zilberbach	2013-10-07 20:38:32
A függvényről még annyit, hogy a továbbiakban egyre kisebb és egyre gyakoribb "ugrálással" emelkedve, aszimptotikusan közelíti a 74 százalék kitöltési tényezőt.
Előzmény: [718] Zilberbach, 2013-10-03 13:32:27

[719] izsák	2013-10-07 09:46:14
Érdekes, hogy két "amatőr" beszélget szimpla matek problémáról, a matematikusok hallgatnak, vagy (ha az eddig válaszolók azok,) akkor hamis válaszokat adnak. Senki nem tudja a választ?
Előzmény: [718] Zilberbach, 2013-10-03 13:32:27

[718] Zilberbach

2013-10-03 13:32:27

Igen, a maximuma x=1 -nél van, akkor a kitöltési tényező = 100

X=1 -től x=1,999... -ig monoton csökken.

x=2 -nél a kitöltési tényező értéke hirtelen fölugrik, majd ismét monoton csökken egészen 3 -ig, ahol megint hirtelen megnő, majd ismét monoton csökken 4 -ig.

A függvény azután is ugrál: egy ideig monoton csökken, azután hirtelen megugrik, majd megint monoton csökken, de már nem csak egész számonként, hanem egyre gyakrabban.

Előzmény: [717] izsák, 2013-10-03 08:32:28

[717] izsák	2013-10-03 08:32:28
Igaz! Ott minimuma van a függvénynek. A maximuma milyen x értéknél lehet? X=1 ? A kettő között és x>2 esetén hogyan alakulhat? Milyen lehet a függvény alakja?
Előzmény: [716] Zilberbach, 2013-10-02 20:24:42

[716] Zilberbach

2013-10-02 20:24:42

Hátha mégis érdekel valakit a válasz (habár így már nyilvánvaló, hogy ez nem nehéz matematikai probléma):

x = 1,9999... értéknél kapjuk a legalacsonyabb kitöltési tényezőt.

Előzmény: [715] Zilberbach, 2013-10-02 11:32:06

[715] Zilberbach

2013-10-02 11:32:06

Ehhez kapcsolódva lenne nekem is egy kérdésem.

Ha a kitöltendő nagy gömb sugara = r, és a kitöltéshez használt kisebb gömbök sugara = r/x, akkor milyen x értéknél kapjuk a legalacsonyabb kitöltési tényezőt?

Előzmény: [705] izsák, 2013-09-25 08:05:38

[714] Erben Péter

2013-10-01 11:55:11

Itt van egy elég alapos történeti áttekintés: http://bib.irb.hr/datoteka/402976.main1.pdf

Ha jól értem, az 1828-as Möbius cikk olyan - elég magas fokszámú - polinomot ad meg, amely kapcsolatot termet az oldalak hossza, a köréírt kör sugara, és a sokszög területe között. (Általában n-oldalú húrsokszögekkel foglalkozott.)

A Robbins-cikket még nem találtam meg, így azt nem tudtam megnézni, hogy adott-e explicit formulát n=5 esetén.

Előzmény: [713] marcius8, 2013-10-01 10:49:59

[713] marcius8	2013-10-01 10:49:59
Köszönöm, hogy foglalkoztál az általam felvetett kérdéssel. Az az igazság, hogy akármit is csináltam, mindig az lett a vége, hogy egy ötödfokú egyenletet kell megoldani. Valószínűleg az általad felírt egyenlet is ötödfokúra vezethető vissza. Tisztelettel: Bertalan Zoltán
Előzmény: [712] w, 2013-09-30 20:11:49

[712] w

2013-09-30 20:11:49

Leírom, hogy szerintem meddig jutottál. :-) Ha egy oldal az r sugarú kör középpontjából $\alpha$ szögben látszódik, akkor hossza 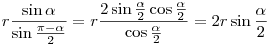$r\frac{\sin\alpha}{\sin\frac{\pi-\alpha}2}=r\frac{2\sin\frac\alpha2\cos\frac\alpha2}{\cos\frac\alpha2}=2r\sin\frac\alpha2$ lesz a szinusz-tétel szerint, vagyis arra van szükség, hogy az a, b, c, d, e oldalakhoz r olyan legyen, hogy

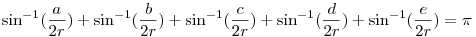$\sin^{-1}(\frac a{2r})+\sin^{-1}(\frac b{2r})+\sin^{-1}(\frac c{2r})+\sin^{-1}(\frac d{2r})+\sin^{-1}(\frac e{2r})=\pi$ fennálljon.

Ez csúnya trigonometriai egyenlet, majd ezt valamelyik algebrista részletezi.

Előzmény: [710] marcius8, 2013-09-30 14:11:41

[711] marcius8

2013-09-30 14:22:12

Ha valaki tud, akkor segítsen a következő feladat megoldásában: Tegyük fel, hogy Európában az UEFA-nak 54 tagállama van (ez majdnem igaz is). Az UEFA a tagállamokat az esedékes labdarugó európa-bajnokság miatt 9 darab selejtező csoportba sorolja, mindegyik csoportban 6 tagállam szerepel. (A csoportokon belül minden tagállam válogatottja játszik minden tagállam válogatottjával otthon is és idegenben is, és csoportokon belül elért eredmények alapján vehetnek részt vagy nem vehetnek részt az európa-bajnokságon.) A következő esedékes labdarugó európa-bajnokság miatt az UEFA a tagállamokat újra 9 darab selejtező csoportba sorolja, mindegyik csoportban továbbra is 6 tagállam szerepel. Mennyi annak a valószínűsége, hogy nincs két olyan tagállam, amely mind a két selejtezősorozatban egymás ellen játszik?

[710] marcius8	2013-09-30 14:11:41
Ha valaki tud, akkor segítsen a következő feladat megoldásában: Ismertek egy húrötszög oldalai, mekkora a húrötszög köré írható kör sugara? Előre is köszönöm bárkinek is a segítségét!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34]

Már regisztráltál?
Új vendég vagy?