|
| [19] lorantfy | 2004-01-12 08:35:54 |
 Kedves Tmbjg!
Alapszabály, hogy kitűzütt feladatokról nem beszélünk itt a fórumon. Általánosságban azt tudom hozzáfűzni az ilyen értelmezésbeli problémákhoz, hogy ha a feladat nem zár ki egy értelmezést akkor azt a lehetőséget is meg kell vizsgálni a megoldásban. Tehát, ha nem vagy biztos benne, hogy a léc csak téglalap keresztmetszetű lehet, akkor vizsgáld meg pl. a trapéz esetet is.
|
| Előzmény: [18] tmbjg, 2004-01-11 21:24:38 |
|
| [18] tmbjg | 2004-01-11 21:24:38 |
 Kedves László, nem tudom jó helyen kopogtatok-e, de egyszerűen nem tudom értelmezni a C.642-es feladatot, ott az áll, hogy egy farönkből vágunk ki "léceket" veszteség nélkül. Eddig úgy tudtam a "léc" keresztmetszete téglalap, de mi van ha trapézre gondolt a feladat írója? Vagy nincs is két párhuzamos oldala?? (Azért nem szeretem az olyan feladatokat amelyek vmilyen konkrét dologról szólnak, amellett hogy ezek állnak legtávolabb a valóságtól, mert mindig nyitva marad egy kérdés ami az egészet zavarossá teszi(: Egy Elkeseredett Versenyző
|
|
| [17] lorantfy | 2004-01-11 11:21:59 |
 Kedves Nádorp!
Nagyon tetszik a megoldásod! A Jensen-egyenlőtlenség nem középiskolás tananyag, de a versenyzők biztosan találkoztak már vele. A könyvajánlóba felteszek egy ügyes kis könyvecskét, amiben többek között ez is szépen le van írva.
Nem haragszol ha kicsit átalakítom a megoldásodat?
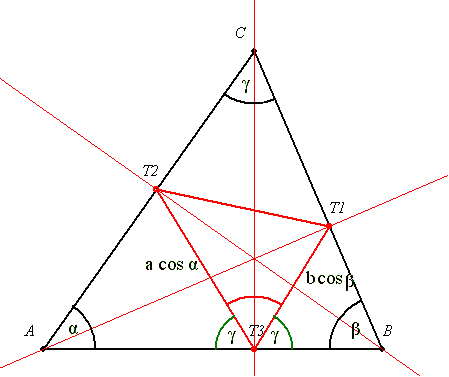
Mivel a levágott háromszögek hasonlóak az eredeti háromszöghöz a talpponti háromszögben:
T2T3=acos  T1T3=bcos T1T3=bcos  AT3T2 AT3T2 =BT3T1 =BT3T1 =180o-2 =180o-2
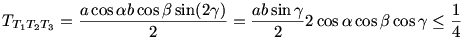
Tehát azt kell csak belátnunk, hogy
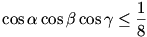
Ehhez pedig elegendő belátni, hogy
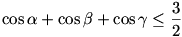
Ugyanis ebből a számtani-mértani közép egyenlőtlenség felhasználásával már következik a szorzatra vonatkozó állítás.
Ez volt a Pest megyei matekverseny utolsó feladata is a 11. évfolyamosoknak:
7. feladat Biz. be, hogy ha  , , , , egy háromszög szögei, akkor egy háromszög szögei, akkor
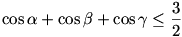
( A Jensen-egyenlőtlenség felhasználása nélkül!)
|
 |
| Előzmény: [16] nadorp, 2004-01-06 12:33:28 |
|
| [16] nadorp | 2004-01-06 12:33:28 |
 Kedves László!
Van egy megoldásom a 6. feladatra, de nem túl szép. A Te ábrád jelöléseit fogom követni, mert az Euklides ( legalábbis a shareware verzió) nekem nem nyerte el a tetszésemet.
Először is könnyű látni, hogy a CT2T1 háromszög hasonló az ABC háromszöghöz, mert a szögeik egyenlőek. (Az ABT1T2 négyszög húrnégyszög, ezért a CAB szög és a T2T1C szögek egyenlőek). Ha  jelöli a C-nél levő szöget, akkor CT2=CBcos jelöli a C-nél levő szöget, akkor CT2=CBcos , ezért a területekre , ezért a területekre 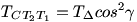 . Ugyanezt megcsinálva az A és B csúcsra is, kapjuk . Ugyanezt megcsinálva az A és B csúcsra is, kapjuk
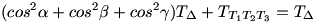 . .
Felhasználva azt a könnyen belátható összefüggést a háromszög szögeire, hogy
(cos2 +cos2 +cos2 +cos2 +cos2 )=1-2.cos )=1-2.cos cos cos cos cos kapjuk, hogy kapjuk, hogy
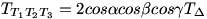
Mivel a cosinus függvény hegyesszögekre pozitív és konkáv, ezért alkalmazva a számtani és mértani közép közti összefüggést utána meg a Jensen egyenlőtlenséget,kapjuk
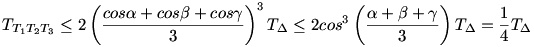
|
| Előzmény: [15] lorantfy, 2004-01-04 13:44:20 |
|
| [15] lorantfy | 2004-01-04 13:44:20 |
 Kedves Fórumosok!
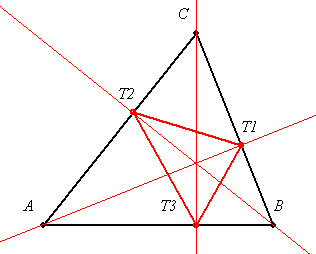
A 3. feladat bizonyításához szükségem lenne egy háromszög és tapponti háromszögének területarányára. Egyenlőre vizsgáljunk hegyesszögű háromszöget!
6. feladat
Biz. be, hogy egy hegyesszögű háromszög talpponti háromszögére:
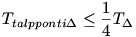
Megjegyzés: A tapponti háromszöget a magasságok tappontjai alkotják.
Egy nevezetes tulajdonsága: A háromszög különböző oldalain lévő három pont által alkotott háromszögek közül ennek a legkisebb a kerülete.
|
 |
| Előzmény: [7] Pach Péter Pál, 2003-12-08 20:11:31 |
|
| [14] lorantfy | 2003-12-30 22:12:51 |
 Kedves Suhanc!
Nagyon jó a térbeli hatszöges példád. Ebből már csak egy lépés az ötszög. Vegyük ki a térbeli hatszög egy élét és a szabadon maradt szakaszvégeket próbáljuk összeérinteni úgy, hogy a többi él között megmaradjon a derékszög. Ezt mutatja a [10] hozzászólás ábrája. A CDE szöget kelleni kiszámítani! A zölddel jelölt szakaszok 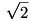 hosszúak. hosszúak.
Azt hiszem ez a versenyfeladatok téma akkor lehetne népszerűbb, ha részeredményeket, ötleteket is megosztanánk egymásssal.
|
| Előzmény: [13] Suhanc, 2003-12-29 17:54:50 |
|
| [13] Suhanc | 2003-12-29 17:54:50 |
 Nem sok eredményem van, de látom, más se küldött megoldást... Az 1. feladat második kérdésére, a térbeli hatszögre a válasz:igen! Tekintsük egy kocka egyik testátlóját. A testátlóhoz tartozó 2 csúcsot, valamint a belőlük kiinduló éleket tüntessük el. A maradék 6 csúcs, és az azokat összekötő 6 él egy olyan térbeli hatszöget határoz meg, amelyre teljesülnek a feladat feltételei.
Az ötszögre egyenlőre nincs ötletem (sejtés: nem lehet), majd gondolkodom rajta...
|
|
| [12] lorantfy | 2003-12-11 13:08:19 |
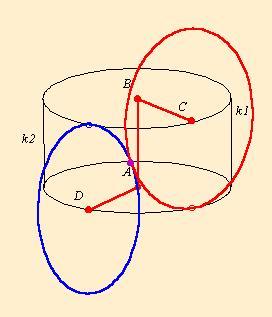
 Ha már megvan az ábra kitaláltam hozzá egy új feladatot. Versenyfeladatnak talán túl könnyű, egy kis térlátási gyakorlat.
5. feladat:
Az ábra szerinti szakaszok AB=BC=AD=r.
k1 egy r sugarú körfűrész, középpontja C. k2 r sugarú körlap, középpontja D.
Milyen idomot vág ki a körfűrész a körlapból, ha
a) a k1 kör C középpontja a B középpontú körön halad végig és közben k2 áll?
b) k1 áll és k2 kör D középpontja az A középpontú körön halad végig, k2 pedig a B középpontú körön gördül?
|
 |
|
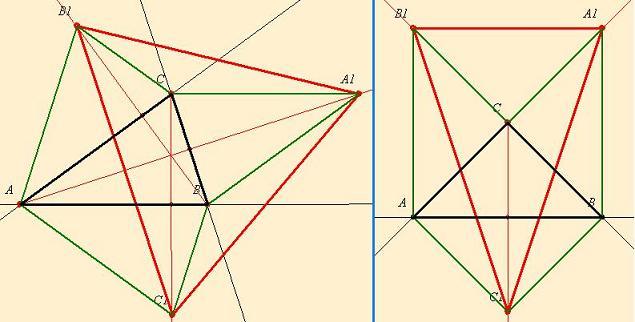
| [11] lorantfy | 2003-12-10 22:09:30 |
 Spec. esetek a 3. feladatnál.
|
 |
|
| [10] lorantfy | 2003-12-10 22:03:47 |
 Kedves Fórumosok!
Jó lenne ha megoldások is érkeznének. Teszek fel pár ábrát az 1. és 3. feladatokhoz, hátha valaki kedvet kap...
|
 |
|
| [9] Rácz Béla | 2003-12-08 22:57:06 |
 Hihetetlen mennyiségű versenyfeladat található meg a következő címen (angolul, sok esetben kidolgozott megoldásokkal):
www.kalva.demon.co.uk
|
|
|
| [7] Pach Péter Pál | 2003-12-08 20:11:31 |
 Még két régi Kürschák-példa:
2. feladat Bebizonyítandó, hogy ha egy háromszög a,b,c oldalaira és szemközti  , , , , szögeire szögeire
a(1-2cos  )+b(1-2cos )+b(1-2cos  )+c(1-2cos )+c(1-2cos  )=0, )=0,
akkor a háromszög szabályos.
3. feladat Egy háromszög csúcsait tükrözzük a velük szemközti oldalegyenesekre. Bizonyítsuk be, hogy az így kapott három pont által alkotott háromszög területe kisebb az eredeti háromszög területének ötszörösénél.
|
|
| [6] lorantfy | 2003-12-08 18:22:51 |
 1. Feladat:
Van-e olyan térbeli ötszög, melynek oldalai egyenlők, és bármely két szomszédos oldala derékszöget alkot? És térbeli hatszög ?
|
|
| [5] lorantfy | 2003-12-07 19:23:15 |
 Kedves Evilcman!
Lehet, hogy igazad van. A "Számelméleti érdekességek" már régebben kivált a fő topicból, meg a biliárdgolyós téma is. Ha neked pl.kedvenced a gráfelmélet nyíss egy külön témát és ha van elég érdeklődő menni fog...Én biztos ott leszek, mert ebben a témában el vagyok maradva.
|
| Előzmény: [4] evilcman, 2003-12-07 18:24:04 |
|
| [4] evilcman | 2003-12-07 18:24:04 |
 Szerintem jobb lenne olyan felosztas hogy pl.:Számelméleti feladatok, Gráfelméleti feladatok stb. mivel úgyis az Érdekes feladatok téma feladatainak a többsége is versenyfeladat volt, és egy ilyen tematikus rendezés sokkal áttekinthetőbb mint több nagyjából ugyanolyan célú topic.
|
|
|
| [2] SchZol | 2003-12-07 14:06:39 |
 Kedves László!
Én is egyet értek veled és Gyurival is, tényleg jobb egy külön téma a versenyfeladatoknak.
Ide csak matek példákat gondoltatok vagy fizikákat is? Csak, mert az Izsák és a Cornides versenynek is voltak fizikából kitűzött feladatai, amit szívesen megosztanék a többiekkel, ha van rá igény, de azokat akkor nem az Érdekes fizika feladatok témába írnám.
Üdv, Zoli
|
| Előzmény: [1] lorantfy, 2003-12-07 13:45:46 |
|
| [1] lorantfy | 2003-12-07 13:45:46 |
 Azért nyitom ezt a témát, mert egyetértek Gyurival abban, hogy:
"Talán attól Érdekes egy feladat, hogy valami szellemesség, csalafintaság, meglepő eredmény vagy humor fűszerezi."
Ez a téma lenne az új és régebbi versenyfeladatoké, kivéve persze az OKTV feladatokat és a lejárt határidejű KÖMAL feladatokat, mert ezeknek már van saját témájuk.
(Arany Dániel, Kürschák József Matematika verseny, Megyei Matekversenyek... jöhetnek ide!)
Ettől föggetlenül persze mindenki abba a témába teszi fel a feladatait, ahová jónak látja!
|
|
