|
| [96] Sirpi | 2009-04-21 15:03:32 |
 Miért lenne igaz, hogy a nevezők és a 110 nem relatív prímek? Pl. a már idézett 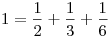 felírásban is relatív prímek a nevezők a 11-hez. Vagy felírásban is relatív prímek a nevezők a 11-hez. Vagy 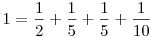 , itt az összeg 22, és a 4 tagból csak 2 nevezővel van közös osztója (könnyű sok ilyen példát generálni, sőt, most látom, hogy #94-ben is van egy 1/3-os tag). , itt az összeg 22, és a 4 tagból csak 2 nevezővel van közös osztója (könnyű sok ilyen példát generálni, sőt, most látom, hogy #94-ben is van egy 1/3-os tag).
Egyébként ha már itt tartunk: szerintetek lehet mondani valamit arra, hogy milyen n összegek bonthatók szét úgy (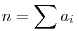 ), hogy ), hogy 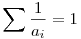 ? ?
Az nyilvánvaló, hogy a négyzetszámok felbonthatók (n2=n+n+...+n), és ha n és m felbontható, akkor n.m is. Ha nem is tudjuk megadni, hogy pontosan mik a jó számok, azért jó lenne valami nem triviális jellemzőjét megadni ennek a halmaznak (pl. sűrűség).
|
| Előzmény: [93] rizsesz, 2009-04-20 14:43:39 |
|
| [95] HoA | 2009-04-21 13:31:06 |
 Az eddigiek alapján mosoly nélkül az a kérdésem: ezt tényleg kitűzték valahol általános iskolai versenyen? Mert kétségtelen, hogy próbálgatással a törtek összeadásának ismeretén felül más nem szükséges hozzá, de vajon a feladat kitűzői hogyan képzelték el a megoldást?
|
| Előzmény: [88] rizsesz, 2009-04-19 22:01:12 |
|
|
| [93] rizsesz | 2009-04-20 14:43:39 |
 gondolom igaz, hogy páronként a nevezők és 110 nem lehetnek relatív prímek. és akkor csak a 2-t tartalmazó megoldásokat kell megtalálni, a többit talán könnyebb :) (tippelgetős agyalgatás...)
|
| Előzmény: [92] Csimby, 2009-04-20 14:34:56 |
|
|
|
|
|
|
| [87] lorantfy | 2009-04-19 15:13:24 |
 Általános iskolai versenyfeladat: Néhány pozitív egész szám összege 110, míg reciprokaik összege 1. Melyek ezek a számok?
|
|
|
|
| [84] lgdt | 2008-06-13 16:24:35 |
 Amúgy az is kijön, hogy ha a bitek száma nem osztható hárommal, akkor minden állapot minden állapotból elérhető. Mi a helyzet n bit esetén, ha egyszerre k szomszédosat módosíthatunk?
|
| Előzmény: [82] lgdt, 2008-06-13 01:05:22 |
|
|
| [82] lgdt | 2008-06-13 01:05:22 |
 2007 osztható hárommal: xoroljuk össze a biteket hármassával: láthatjuk, hogy az eredmény mindhárom bitje lépésenként negálódik, tehát ha két állásnál A és B az eredmény, akkor ha A^B != 0, az állások egymásból elérhetetlenek.
|
| Előzmény: [80] S.Ákos, 2008-04-19 20:25:27 |
|
| [81] teodóra | 2008-04-20 15:35:49 |
 Elnézést, nem tudja valaki, hogy hol találom meg az előző Szőkefalvi döntők feladatsorait, vagy a tavalyi Bács-Kiskun megyei végeredményt?
|
|
| [80] S.Ákos | 2008-04-19 20:25:27 |
 Csütörtökön volt AranyDani döntő: egy aranyos, de nem túl nehéz feladat:
Egy szabályos 2007-szög csúcsaiba + vagy - jeleket írunk. Egy lépés során 3 szomszédos csúcshoz rendelt jelet a másikra változtatjuk. Van-e olyan színezés, amiből nem érhető el az az állás, mikor minden csúcsban + jel áll?
|
|
|
| [78] Csimby | 2008-02-24 23:08:53 |
 Senki sem kételkedett benne hogy Te meg tudod csinálni a feladatot, nyilván nem neked írtam be, de te nem is 10.-es vagy ;-) Másnak talán érdekes lehetett volna ha nem írod be rögtön mit kell csinálni, de a lényeg tényleg a következő: an+1+1=(ak+1)2(1-2ak+3ak2) Szerintem ez egy teljesen jó feladat 10.-es versenypéldának.
|
| Előzmény: [75] Róbert Gida, 2008-02-21 23:51:44 |
|
| [77] Róbert Gida | 2008-02-24 17:37:20 |
 Tévedsz. Kettő darab A feladat megoldását raktam fel ebben a tanévben. Nem nehéz eltéveszteni, egymásutáni hozzászólások voltak a "Lejárt határidejű KÖMAL feladatokról" című topikban. Egyébiránt ahogy elnéztem azt a topikot csak én raktam fel A megoldást ebben a tanévben.
Az meg, hogy könnyűek az A feladatok nem tehetek róla. Fordulj Kós Gézához, ő találja ki őket.
|
| Előzmény: [76] rizsesz, 2008-02-22 08:52:41 |
|
| [76] rizsesz | 2008-02-22 08:52:41 |
 Úgy gondolod Róbert Gida, hogy ez egy triviális példa? Szerintem nem az. Ahogyan nem is értem, hogy miért csak egy A-t tettél fel megoldással ide a határidő lejárta után (ami persze lényegesen könnyebb volt, mint a többi).
|
|
|
| [74] Csimby | 2008-02-21 21:24:54 |
 Sziasztok! Ma volt Arany Dani III.kat. az első feladat nekem nagyon tetszett: a0=9 és ak+1=3ak4+4ak3 Biz. be, hogy a10 legalább 1000 db kilences számjegyre végződik.
|
|
|
