|
| [1144] HoA | 2008-11-10 11:43:00 |
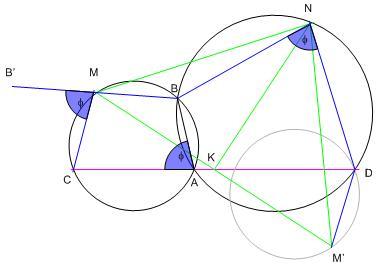
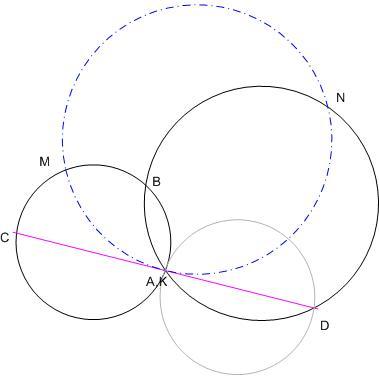
 A 141.feladat megoldása: Tükrözzük M-et K-ra, a tükörkép legyen M' .
a) Vegyük fel BM meghosszabbításaként az MB' = BM szakaszt. Jelöljük a BND szöget  -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is  . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja  -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja  -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
b) Felhasználjuk, hogy egy X pont körüli  szögű és egy Y pont körüli szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli szögű elforgatás eredője egy Z pont körüli  + + szögű elforgatás, speciálisan ha szögű elforgatás, speciálisan ha  + + = = , akkor egy Z pontra vonatkozó tükrözés. CMB szög = , akkor egy Z pontra vonatkozó tükrözés. CMB szög =  - - , az M körüli , az M körüli  - - szögű elforgatás C-t B-be viszi, az N körüli szögű elforgatás C-t B-be viszi, az N körüli  szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
|
 |
| Előzmény: [1143] BohnerGéza, 2008-11-05 23:18:14 |
|
| [1143] BohnerGéza | 2008-11-05 23:18:14 |
 A "kis segítség" önnálló feladatnak biztosan jó, ajánlom mindenkinek!
A 141. feladatra két megoldást ismerek, azokhoz nem használtuk ezt a segítséget, talán egy harmadikhoz jó.
Az általam ismett megodások alapszava:
- - - egyikhez: "ha felező..., akkor tükrözzünk rá!"
- - - másikhoz: "leképezések"
|
| Előzmény: [1142] HoA, 2008-11-05 11:24:39 |
|
|
| [1141] BohnerGéza | 2008-10-31 00:06:46 |
 A zalaegerszegi Zrínyi Miklós Gimnázium "IZSÁK IMRE GYULA" komplex természettudományi versenyének egyik szép feladatát ajánlom.
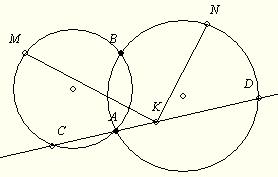
141. feladat: A k1 és k2 kör két pontban, A-ban és B-ben metszik egymást. Legyen C a k1-nek k2-n kívüli olyan pontja, melyre a CA egyenes k2-t olyan az A-tól különböző D pontban metszi, mely nincs a k1-en belül. Továbbá legyen K a CD, M a k1 A-t nem tartalmazó BC ívének és N a k2 A-t nem tartalmazó DB ívének felezőpontja. Bizonyítandó, hogy MKN szög derék!
|
 |
|
| [1140] HoA | 2008-10-26 23:06:36 |
 Pedagógiailag nagyon jó feladatnak tartom. Szinte vonzza a szemet, hogy AC felezőpontját E és G között NEM jelöli az F betü. Honnan ismerős a szakaszt két oldalról érintő két kör, ráadásul az ábra alapján a szakasz felezőpontjára szimmetrikus két pontban? Először belátjuk, hogy ez nem csak ránézésre van így, hanem a [1139] - beli egyenlőség éppen a feladat feltételeiből következik. És ami még "hiányzik" az ábráról: ABC beírt k1 körének E-vel átellenes H pontja - és ugyanígy ACD beírt k2 körének G-vel átellenes I pontja , melyek úgy tűnik, rajta vannak BG-n illetve DE-n. Végül az ABC háromszög AC oldalát G-ben érintő hozzáírt k3 kört megrajzolva teljes az ábra. Így már jól láthatóak a beírt és hozzáírt körök vizsgálatánál megismert hasonlóságok. k1 és k3 külső hasonlósági pontja B, ezért B, H és G valóban egy egyenesen van. k1 és k2 külső hasonlósági pontja P, ezért P, G és H egy egyenesen van. Vagyis P, G, H, B egy egyenes pontjai. És persze ugyanez áll P, D, I, E -re.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
|
| [1138] HoA | 2008-10-20 08:50:44 |
 Két előzetes megjegyzés:
1) Nem nyilvánvaló kapcsolatot találni egy ábra bizonyos pontjain átmenő körök középpontjai és az ábra többi része között. Az itt célravezető meglátás: két egymást metsző kör centrálisa merőleges a közös húrra. Ezt a bizonyításban többször is felhasználjuk.
2) Ha sikerül bebizonyítnai, hogy tetszőleges három körülírtkör-középpont a körülírt körök közös M pontjával egy körön van, akkor egyúttal azt is bizonyítottuk, hogy a négy körülírt kör középpontja és M egy körön van, hiszen például ha O1,O2,O3ésM egy körön van , valamint O1,O2,O4ésM egy körön van, akkor ez úgy is fogalmazható, hogy O3ésO4 is rajta van az O1,O2 és M ponthármas által meghatározott körön.
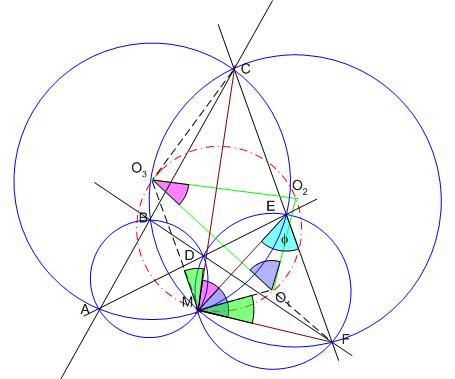
[1136] ábráját megbetűzve MF merőleges O1O2 -re, ME merőleges O1O3 -ra , így nem egymás szögtartományába eső merőleges szárú szögek lévén FME =O2O1O3 =O2O1O3 . Hasonlóan adódik, hogy EMC . Hasonlóan adódik, hogy EMC =O1O3O2 =O1O3O2 . A kettőt összegezve FMC . A kettőt összegezve FMC O3O2O1 O3O2O1 kiegészítő szögével egyenlő. kiegészítő szögével egyenlő.
Jelöljük az MEF -et -et  -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú  -ben -ben  a középponti szög, MO1F a középponti szög, MO1F fele, így FMO1 fele, így FMO1 = = /2- /2- . .
Az O3 középpontú k3 körben CEM = = - - a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög  , az MCO3 egyenlőszárú , az MCO3 egyenlőszárú  -ben -ben  a középponti szög, MO3C a középponti szög, MO3C fele, így CMO3 fele, így CMO3 = = /2- /2- . .
O1MO3 =FMC =FMC -FMO1 -FMO1 +CMO3 +CMO3 =FMC =FMC , az O3O2O1 , az O3O2O1 kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak. kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak.
|
 |
| Előzmény: [1136] BohnerGéza, 2008-10-16 19:03:53 |
|
|
|
| [1135] BohnerGéza | 2008-10-12 01:28:32 |
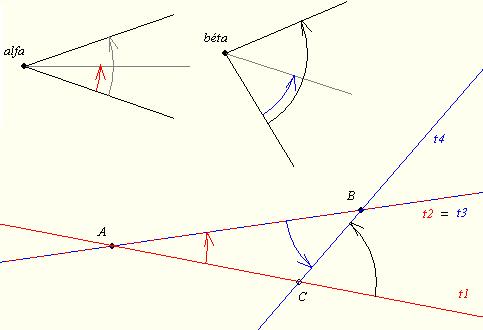
 140/b feladat: Bizonyítandó, ha a 140. feladatban az ABCD négyszög konkáv, akkor az állítás - ha vannak - a közös belső érintőkkel, igaz! ( Szóval a BG és DE átmegy a körök belső hasonlósági pontján. )
Megjegyzés: Ha a 140-ben a két kör sugara egyforma, akkor BG és DE párhuzamos a centrálisukkal.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
| [1134] BohnerGéza | 2008-10-12 01:13:22 |
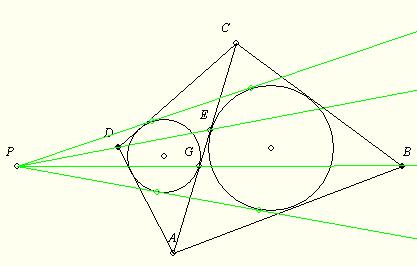
 140.feladat: A konvex ABCD négyszögben DA+AB=BC+CD-vel. (Nem érintőnégyszög!) Az ABC háromszög beírt köre érintse AC-t az E, a BDA-é a G pontban. Bizonyítandó, hogy a beírt körök közös külső érintői, a BG és a DE egyenesek egy ponton mennek át!
|
 |
|
| [1133] sakkmath | 2008-10-05 16:13:09 |
 Kérdéseddel dr. Dályay Pál Péterhez, a szegedi Deák Ferenc Gimnázium tanárához célszerű fordulni. A feladatot az ő javaslatára a The American Mathematical Monthly tűzte ki 2006-ban 11240-es sorszámmal. A 2008. évi februári szám internetes hivatkozása itt már a rövidített megoldást is közli.
|
| Előzmény: [1132] Lóczi Lajos, 2008-10-03 21:21:38 |
|
| [1132] Lóczi Lajos | 2008-10-03 21:21:38 |
 Az exponenciális függvény konvexitása miatt minden valós x-re 1+x ex. Speciálisan, ha x ex. Speciálisan, ha x (0,1), akkor 1-x (0,1), akkor 1-x e-x, így e-x, így 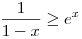 . Legyen most . Legyen most 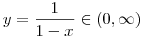 tetszőleges, ekkor tetszőleges, ekkor 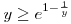 . Végezzük itt el az . Végezzük itt el az 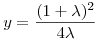 helyettesítést, ha helyettesítést, ha  >0 tetszőleges. Azt kapjuk, hogy >0 tetszőleges. Azt kapjuk, hogy 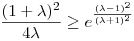 . Legyen most . Legyen most 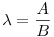 , ha A>0 és B>0 tetszőleges. Ekkor , ha A>0 és B>0 tetszőleges. Ekkor 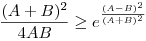 . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy 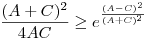 és és 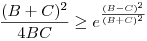 is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re
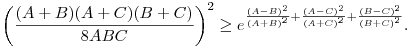
Vonjunk gyököt az egyenlőtlenségből, majd végezzük el az A=a+b-c>0, B=a-b+c>0, C=-a+b+c>0 helyettesítéseket, ahol a, b és c a háromszög oldalai. Azt kapjuk, hogy
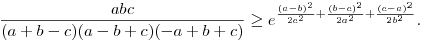
A fenti bal oldal viszont éppen 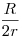 . .
Amúgy honnan jött ez az állítás? (Valami hiperbolikus/abszolút geometriai tétel?)
|
| Előzmény: [1131] sakkmath, 2008-10-03 13:36:48 |
|
|
| [1130] Káli gúla | 2008-10-01 16:36:48 |
 Ha K a a háromszög symmediáns pontja és O a köré írt kör középpontja, akkor a Tucker körök középpontjai éppen az OK szakasz pontjai. A bizonyítás megtalálható pl. W. Mclelland: A Treatise On The Geometry Of The Circle. Macmillan, 1891. könyvében a 73. oldalon. A könyv olvasható, és le is tölthető a www.archive.org oldalon, csak rá kell keresni a címére.
|
| Előzmény: [1128] klerox, 2008-09-30 17:45:13 |
|
|
| [1128] klerox | 2008-09-30 17:45:13 |
 A Tucker körnek a lényege: Feltétel: A'A"=B'B"=C'C", és A'A", B'B" és a C'C" antiparallel a BC, CA és AB oldalakkal. A hat pont: A', A", B', B", C' és C" egy körön helyezkedik el. Tudomásom szerint kell középpontjának lenni.
|
|
| [1127] BohnerGéza | 2008-09-29 22:40:25 |
 Biztos, hogy nem a "Matematikus-fizikus viccek, sztorik" közé akartad írni?
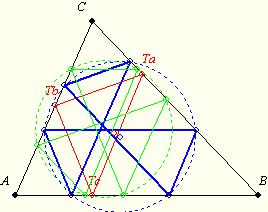
Utána néztem, a Tucker-kör vszleg hatszög, azaz önmagába visszatérő vonal. Ilyet a talpponti háromszög (piros) segítségével is meg lehet szerkeszteni. Az ábrán kettő látszik (kék, zöld) és nyilván végtelensok van. Mivel ezen hatszögek köré írható kör, de ezek kp-jai nem esnek egybe, nincs értelme a kérdésnek.
|
 |
| Előzmény: [1126] klerox, 2008-09-29 19:30:34 |
|
| [1126] klerox | 2008-09-29 19:30:34 |
 Sziasztok!
A Tucker-kör megszerkesztésével bajlódok, de sehogy nem jövök rá a középpont megszerkesztésére, kérlek segítsetek.
Előre is köszönöm
|
|
| [1125] BohnerGéza | 2008-09-24 11:16:44 |
 Ismert a következő: Ha négy egyenes négy háromszöget határoz meg, akkor ezek körülírt körei átmennek egy közös ponton.
138. feladat: Bizonyítandó, hogy a négy körülírt kör középpontja és ez a közös pont egy körön van.
|
|
|
| [1122] Sirpi | 2008-09-08 13:41:42 |
 Nemrég nekem is szükségem volt hasonló programra, csak éppen gömbközéppontot kellett keresni felületi pontok alapján, és írtam egy egyszerű módszert, ami a tesztek alapján elég jól működik, röviden le is írom, hogyan (körre is jó változtatás nélkül):
Legyenek adva a P1,P2,...,Pn pontjaink, és keressük az O középpontot iterációs módszerrel. Legyen O0 a megadott Pi ponthalmaz súlypontja. Ha egyenletes a ponteloszlás, akkor ez már önmagában is majdnem jó, de ha nem, akkor is egy jó kiindulópont.
Nézzük a k+1. lépést: rendezzük sorba a Pi pontokat az Ok-tól vett távolság alapján, és a robusztusság miatt ebből hagyjuk el a legközelebbi és a legtávolabbi 10%-ot, legyen ez első meghagyott pont R (tehát ez egy majdnem legközelebbi pont Ok-hoz képest), az utolsó S (ez pedig a majdnem legtávolabbi, leszámítva a felső 10%-ot). Ideális esetben Ok-t az RS szakasz felezőmerőlegesére kellene "ráhúzni", de tapasztalataim alapján így lassabb a konvergencia, mintha csak a felezőmerőlegeshez képest a felére csökkentenénk a távolságot. Tehát ha Ok talppontja RS felezőmerőlegesére T, akkor Ok+1-nek válasszuk Ok és T felezőpontját, majd folytassuk az eljárást.
Megállási feltétel: Egy adott Ok pont jóságát mérjük az |SOk|-|ROk| különbséggel, és ha ez kisebb, mint az eddigi legjobb, akkor jegyezzük meg ezt, mint lehetséges végső kör/gömbközéppontot. És ha mondjuk 1000 iterációs lépésen keresztül ez a rekord nem dől meg, akkor legyen ez a végső győztes is egyben.
|
| Előzmény: [1121] farkasb, 2008-09-08 00:49:03 |
|
| [1121] farkasb | 2008-09-08 00:49:03 |
 Kedves "Fálesz" Mihály!
Visszatérve a legjobban illeszkedő körhöz... Sajnos nem tudom végigszámolni a kör a megadott segédletek alapján, elakadok vele..Az a baj,hogy nem teljesen látom át. Örülnék ha egy konkrét példán bemutatott feladatmegoldást láthatnék.
Van egy programom, ami képes erre a legjobban illeszkedő kör készítésére, a megadott pontokra az alábbi eredmények számolja:
Adottak az alábbi pontok (X,Y):
(0,1000); (10,1000); (400,4000); (500,2000); (-500,-1500); (-900,-3500); (-7000,-3500);
Eredmények(origó,sugár):
X0= -4853.3 ; Y0= 1209.7 ; R= 5352.6 ;
Távolságok az origótól:
1=4857.8; 2=4867.8; 3=5948.4; 4=5411.3; 5=5127.7; 6=6149.0; 7=5175.8;
Amennyiben nem túl nagy munka a segítség, megköszönném. Ha nagy, akkor sincs semmi gond :) Előre is köszönettel: farkasb
|
| Előzmény: [1111] Fálesz Mihály, 2008-09-02 21:45:36 |
|
| [1120] Sirpi | 2008-09-07 11:22:30 |
 Mivel semmi más adat nincs megadva a két egyenesen kívül, ezért nem nagyon jutott eszembe más lehetöség, hogy mi lehet a feladat. Felsoroltam azt a 2-t, ami viszont igen :-)
|
| Előzmény: [1118] jonas, 2008-09-03 22:25:25 |
|




 -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is
-vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is  szögű és egy Y pont körüli
szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli
szögű elforgatás eredője egy Z pont körüli  , akkor egy Z pontra vonatkozó tükrözés. CMB szög =
, akkor egy Z pontra vonatkozó tükrözés. CMB szög = 

 =O2O1O3
=O2O1O3 -ben
-ben 




 ex. Speciálisan, ha x
ex. Speciálisan, ha x (0,1), akkor 1-x
(0,1), akkor 1-x >0 tetszőleges. Azt kapjuk, hogy
>0 tetszőleges. Azt kapjuk, hogy 



