| [1284] sakkmath | 2009-09-27 11:32:04 |
 4/b. feladat: Szerkesszük meg a két ellipszis érintkezési pontjaihoz tartozó érintőit!
(Ez a részfeladat - a szerkesztési eljárást bemutató - bizonyítandó állítás formájában is megfogalmazható. Ez viszont könnyítést jelenthetne, s esetleg elrontanám vele a megoldó(k) örömét ...)
|
| Előzmény: [1283] sakkmath, 2009-09-26 17:52:54 |
|
|
|
|
| [1280] PuzzleSmile | 2009-09-25 10:34:31 |
 A puzzle 4 darabja még hiányzik, az egyikük rajzos. Ha holnap sem lesz, aki kirakja őket, vasárnap ezt megteszem én. (Ezek jelentősége már kisebb.)
A (1276)-os "foltozás" nem inverziós, de az eredeti első bekezdés meghagyásával létezik inverziós befejezés is. Igaz, ez keverék megoldást ad és elromlik a szimmetria.
|
| Előzmény: [1278] HoA, 2009-09-25 06:56:37 |
|
| [1279] BohnerGéza | 2009-09-25 09:54:02 |
 Mint írtam:
"Az adott inverzióval játszva sok érdekességet láthatunk, kár, hogy a megoldásnál fölösleges!"
Azaz kár, hogy a megoldásnál fölösleges az inverzió!
|
| Előzmény: [1278] HoA, 2009-09-25 06:56:37 |
|
| [1278] HoA | 2009-09-25 06:56:37 |
 Köszönöm PuzzleSmile-nak, hogy ismát ráirányította figyelmemet erre a megoldásra. Azt ugyan még nem árulta el, hogy hol a puzzle, de rájöttem, hogy ha már angolkodunk, akkor ez inkább joke. Ugyanis nem inverziós megoldás. Az első bekezdés helyett nyugodtan írhattuk volna: "Húzzunk párhuzamost M-en át BC-vel, az AB-vel alkotott metszéspont legyen L*. " Ettől persze még a bizonyítás helyes.
|
| Előzmény: [1275] PuzzleSmile, 2009-09-23 11:05:28 |
|
|
| [1276] HoA | 2009-09-23 21:38:59 |
 Ha az ábrát kell szerinted kiegészíteni, áruld el, mire gondolsz. Ha a megoldás szövegét nem találod teljesnek, olvasd el a téma utolsó néhány heti hozzászólásait, melyek alapján az inverzió jópár tulajdonságát már ismertnek vesszük. Azt meg, hogy ML és BC párhuzamosságából következik LN és BC párhuzamossága, úgy értjük, mint [1270] végén: A C1re leírtakat B1re vonatkoztatva kapjuk, hogy MN és BC párhuzamos, tehát L,M,N egy egyenesen vannak és ez párhuzamos BC-vel.
|
| Előzmény: [1275] PuzzleSmile, 2009-09-23 11:05:28 |
|
|
| [1274] BohnerGéza | 2009-09-19 23:10:15 |
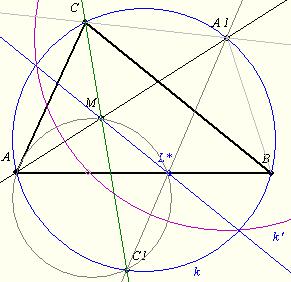
 Legyen az inverzió az az A1 középpontú kör, melyre az A képe M. Ekkor a „k” körülírt kör képe az M-en átmenő BC-vel párhuzamos k’ egyenes. (A1 felezi a BC ívet.) Jelölje L* az AB és k’ metszéspontját.
Mivel C1-ből és L*-ból is béta szögben látszik az AM szakasz, az A, a C1, a L* és az M egy körön van. Ebben a körben a L*M és k-ban az A1C ív is alfa/2 szögben látszik, ezért C1, L* és A1 egy egyenesen van, azaz L* azonos L-lel. Ebből következik, hogy LN átmegy M-en és párhuzamos.
(Az adott inverzióval játszva sok érdekességet láthatunk, kár, hogy a megoldásnál fölösleges!)
|
 |
| Előzmény: [1266] sakkmath, 2009-09-11 16:16:11 |
|
|
|
| [1271] sakkmath | 2009-09-19 18:19:39 |
 Köszönöm Hoa szép megoldását. Úgy látszik, nincs több hozzászóló, ezért - két részletben - fölteszem saját inverziós levezetésemet, amely különbözik [1270]-től. Az 1. rész:
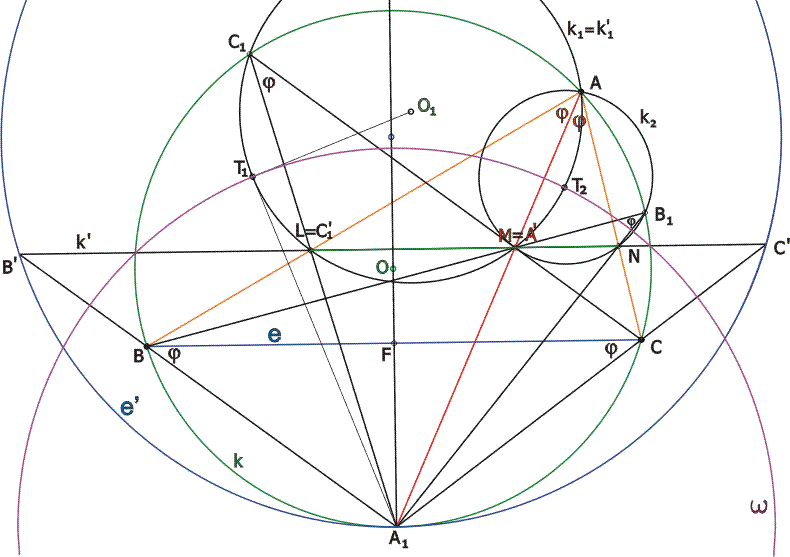
Az ABC háromszög körülírt köre k, középpontja O, a háromszög A csúcsában lévő szög 2 . Az AA1 szögfelező felezi a 2 . Az AA1 szögfelező felezi a 2 szöget, ezért A1AB szöget, ezért A1AB = CAA1 = CAA1 = =  , másrészt a BA1 húron nyugvó kerületi szögek egyenlőségéből A1AB , másrészt a BA1 húron nyugvó kerületi szögek egyenlőségéből A1AB = A1B1B = A1B1B =A1CB =A1CB = =  . Az A1C húron nyugvó kerületi szögekre: CAA1 . Az A1C húron nyugvó kerületi szögekre: CAA1 = CC1A1 = CC1A1 = CBA1 = CBA1 = =  . Látható, hogy az LM szakasz a C1 és az A pontból egyaránt . Látható, hogy az LM szakasz a C1 és az A pontból egyaránt  szög alatt látszik. Ezért az L, M, A, és C1 pontok egy k1 körön sorakoznak, melynek középpontja O1. szög alatt látszik. Ezért az L, M, A, és C1 pontok egy k1 körön sorakoznak, melynek középpontja O1.
|
 |
| Előzmény: [1266] sakkmath, 2009-09-11 16:16:11 |
|
| [1270] HoA | 2009-09-15 22:45:37 |
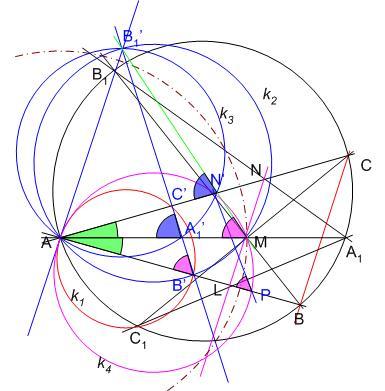
 Legyen az inverzió alapköre az A középpontú, AM sugarú kör. Az inverz pontokat jelöljük vesszőzve. A körülírt kör képe egyenes, ezen jelöljük meg B’,C’,A1’ésB1’ pontokat. BC egyenes képe az AB’C’ pontokon át húzott k1 kör, BB1 képe az AB’MB1’ pontok k2 köre, A1B1 képe, k3 , AA1’N’B1’ pontokon halad át, végül legyen k4 kör az MN egyenes képe az AMN’ pontokon át. BAA1 =A1AC =A1AC = = /2 . B1’A1’A /2 . B1’A1’A =B1’N’A =B1’N’A (k3 –ban közös húr ) . B1’B’A (k3 –ban közös húr ) . B1’B’A =B1’MA =B1’MA (k2 –ben közös húr ) . Ezért B1’M egyenes az AC és AA1 egyenesekkel AB’A1’ höz hasonló háromszöget alkot, ennek külső szöge megegyezik B1’N’A (k2 –ben közös húr ) . Ezért B1’M egyenes az AC és AA1 egyenesekkel AB’A1’ höz hasonló háromszöget alkot, ennek külső szöge megegyezik B1’N’A -gel, B1’,N’ésM egy egyenesen van. Legyen AB és k4 másik metszéspontja P. N’PA -gel, B1’,N’ésM egy egyenesen van. Legyen AB és k4 másik metszéspontja P. N’PA =N’MA =N’MA =C’B’A =C’B’A . AB’C’ és APN’ hasonló háromszögek, egymásból A középpontú nyújtással keletkeznek. Ez igaz körülírt köreikre is. A tehát k1 és k4 hasonlósági pontja, a két kör érinti egymást. Szimmetrikus módon a C1’ -n áthaladó inverz körök vizsgálatával kapjuk, hogy az ML egyenes képe is a k1 kör A középpontú nyújtásával keletkező, M-en áthaladó kör, vagyis k4 ( és P = L’ ) . L,M, N egyazon egyenes pontjai, és mivel k1 -nek és k4 nek nincs A-tól különböző közös pontja, inverz képeik, a BC és LN egyenes párhuzamosak. . AB’C’ és APN’ hasonló háromszögek, egymásból A középpontú nyújtással keletkeznek. Ez igaz körülírt köreikre is. A tehát k1 és k4 hasonlósági pontja, a két kör érinti egymást. Szimmetrikus módon a C1’ -n áthaladó inverz körök vizsgálatával kapjuk, hogy az ML egyenes képe is a k1 kör A középpontú nyújtásával keletkező, M-en áthaladó kör, vagyis k4 ( és P = L’ ) . L,M, N egyazon egyenes pontjai, és mivel k1 -nek és k4 nek nincs A-tól különböző közös pontja, inverz képeik, a BC és LN egyenes párhuzamosak.
|
 |
| Előzmény: [1266] sakkmath, 2009-09-11 16:16:11 |
|
| [1269] sakkmath | 2009-09-14 12:21:57 |
 Az archaikus szövegből kihámozható, hogy az Euler-egyenessel kapcsolatos ismert tételről van szó. Olvassuk el itt Dr. Darvasi Gyula: Egy feladat - többféle megoldás című doktori értekezésének 1.5 fejezetét (a 83. oldalon kezdődik, Egy oldallal párhuzamos Euler-egyenes címmel).
Remélem, jó a következtetésem. Az egyes kifejezések modernizálását meghagyom a következő hozzászólónak :)
|
| Előzmény: [1268] jeneit92, 2009-09-12 08:46:28 |
|
| [1268] jeneit92 | 2009-09-12 08:46:28 |
 Sziasztok,találtam egy nagyon érdekes feladatot,ami szerintem a geometriához kapcsolódik: Az tiszta tudékosságban járatos Euler professor Urunk nevezetes léniájárúl Lészen ollybá egy háromszeglemény , melliknek is nehézkedési czentrálisán s ortogonális czentrálisán is által visitáló léniája paralell vala egyvalamely gyepüléniával.Igazoltassák,hogy emez gyepülénia kenyekinek kebeljeinek szorzamányát pótkebeljeinek szorzmányával hányadékul véve mindenkoron 3 adatik.Vajon igaz vala-é az fentebb forgandó theoria visszásítása?" (Gerőcs László Tanár Úr: XVII. századi matekóra című előadásának egy feladata alapján.
Ha bárkinek van ötlete,javaslata,megoldása örömmel veszem,köszi előre is
|
|
|
| [1266] sakkmath | 2009-09-11 16:16:11 |
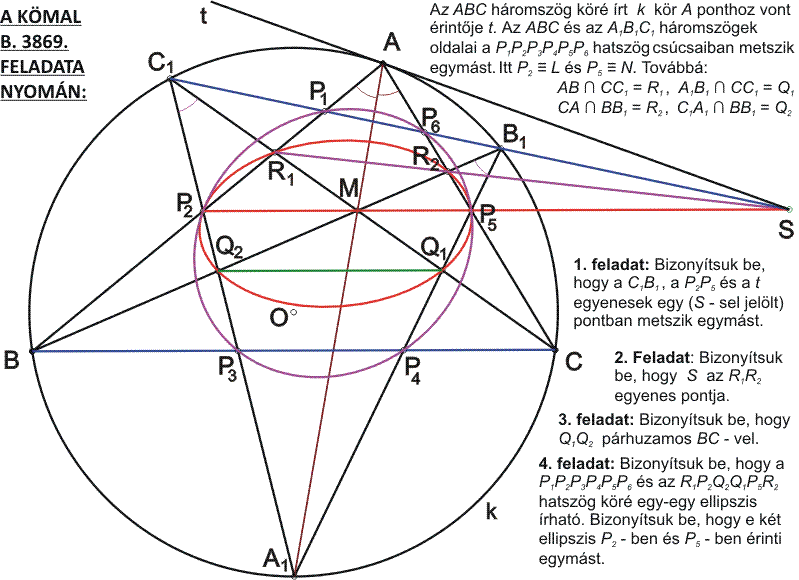
 Az elmúlt hónap hozzászólásainak gyakori témája a körre vonatkozó inverzió. Oldjuk meg inverzióval a KöMaL 2005 decemberi számának következő feladatát:
B. 3869. Az ABC hegyesszögű háromszög belsejében, az A csúcsból induló szögfelezőn felvettük az M pontot. Az AM, BM, CM egyeneseknek a körülírt körrel való második metszéspontja rendre A1, B1 és C1. Az AB és a C1 A1 egyenesek az L pontban, az AC és a B1 A1 egyenesek az N pontban metszik egymást. Bizonyítsuk be, hogy az LN szakasz párhuzamos BC-vel.
(A Lap nem közölt inverziós megoldást.)
|
|
| [1265] HoA | 2009-09-08 09:34:39 |
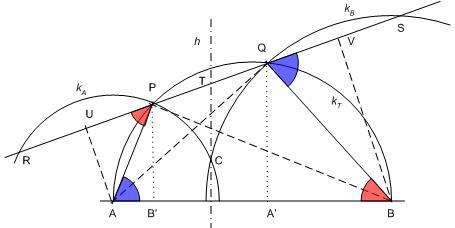
 BohnerGéza utólagos engedelmével legyen ez a 156. feladat . Vegyük észre, hogy ez a 154/b feladat általánosításának tekinthető. C-nél derékszögű ABC háromszögre megegyezik a [1260]-ban kitűzött és megoldott 154/b feladattal – pontosabban annak megfordítottjával. Ha ABC C csúcsú egyenlőszárú háromszög, akkor a feladatban szereplő alakzatok szimmetrikusak a C-nél lévő szög felezőjére, a megoldás evidens. Legyen tehát AC < BC.
Először legyen ABC C-nél tompaszögű – a hegyesszögű esetet várom a további érdeklődőktől. C ekkor AB kT Thálesz-körének belső pontja. Az A középpontú C-n átmenő kA kör és kT metszéspontja P, a B középpontú C-n átmenő kB kör és kT metszéspontja Q. A PQ egyenes kA-t még R-ben, kB-t még S-ben metszi. Legyen PR felezőpontja U, QS felezőpontja V. ABQP húrnégyszög. Az ábrán kékkel ill. pirossal jelölt szögeket tartalmazó derékszögű háromszögek hasonlóságából:
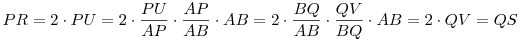
. Így PQ T felezőpontjának kA-ra és kB-re vonatkozó hatványa megegyezik, T rajta van kA és kB hatványvonalán, a C-n áthaladó AB-re merőleges h egyenesen . P merőleges vetülete AB-n B’, Q-é A’ . A’B’PQ derékszögű trapéz, TC a középvonala, A’B’ felező merőlegese. A’ és B’ egyenlő távolságra van C-től. Ha valakinek nem világos, hogy A’ és B’ a feladatban szereplő inverz képek, vessen egy pillantást [1258] ábrájára.
|
 |
| Előzmény: [1263] BohnerGéza, 2009-09-05 01:06:08 |
|
| [1264] BohnerGéza | 2009-09-05 19:38:50 |
 Ez az eredetileg az [1246]-ban kitűzött, majd részleteiben belátott feladatnak egy letisztult bizonyítása a beírt körre. Javaslom a végiggondolását a hozzáírt kör esetére!
154. feladat: Az ABC háromszögben vegyük az A-hoz kapcsolható két érintőkör egyikét - vagy a beírt kört, vagy az A-val szemközti hozzáírt kört - és annak középpontját. Igazoljuk, hogy az ezen középponton átmenő A középpontú alapkörre vonatkozó inverziónál az ABC körülírt körének képe érinti az érintőkört!
|
 |
| Előzmény: [1252] BohnerGéza, 2009-08-13 13:55:33 |
|
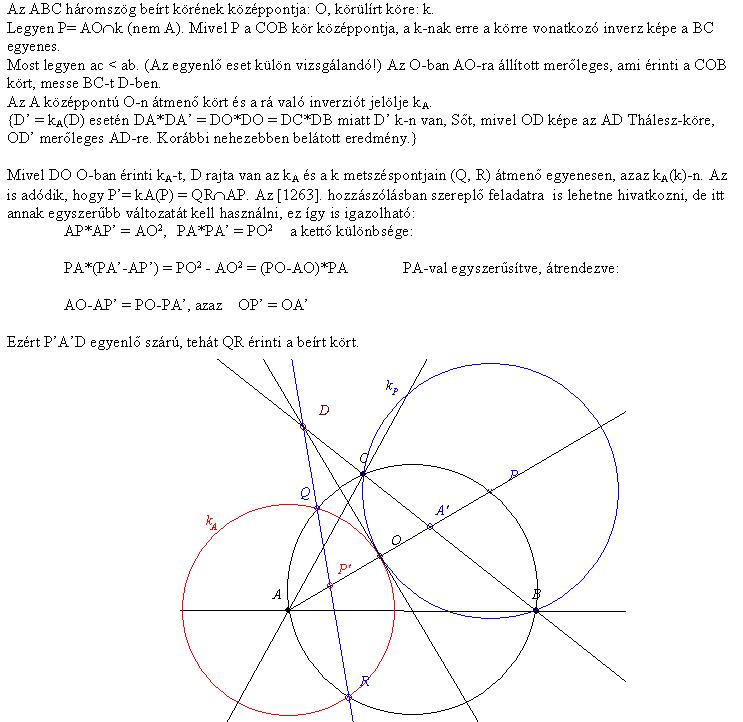
| [1263] BohnerGéza | 2009-09-05 01:06:08 |
 Tetszőleges A, B és C esetén legyen A' a A-nak inverz képe a B középpontú C-n átmenő körre, B' a B-nek inverz képe az A középpontú C-n átmenő körre.
Bizonyítandó, hogy CA'=CB'.
|
|
| [1262] BohnerGéza | 2009-08-27 17:46:46 |
 Mivel a négy háromszög tétel, amire HoA [1260]-ban utal, nem ismert, bár a Fórumban már szerepelt:
Ha négy egyenes négy háromszöget határoz meg, akkor ezek körülírt körei egy ponton mennek át és magasságpontjaik egy egyenesen vannak.
(Azt most nem gondoltam át, hogy ennek használata egyszerűsítheti-e az [1252]-ben írtakat.)
Érdekes következménye ennek: Ha adott egy parabola négy érintője, akkor mivel ezek négy háromszöget határoznak meg, a fókuszt és a vezéregyenest kapjuk.
|
| Előzmény: [1260] HoA, 2009-08-27 14:53:48 |
|
| [1261] BohnerGéza | 2009-08-27 17:35:04 |
 HoA [1261] jogos felvetései alapján írom.
Az IA és ID az [1252]-es hozzászólásban meghatározott inverziók. A 154. feladat és vázlatos megoldása is ott szerepel, annak a kiegészítése ez. Belátjuk, hogy O a két alapkör metszéspontja.
A D’-n átmenő AD-re merőleges m egyenes IA-nál és ID-nél is az AD Thálesz-köre, ezért ennek a körnek és m-nek a metszéspontja mindkét inverzió alapkörén van.
Jelölje P az AO egyenes és az ABC kör (nem A) metszéspontját. Bizonyítható középponti-kerületi szögekkel, hogy P az OBC kör középpontja. A DO érinti ezt a kört: DO négyzete = DC*DB = DD’*DA, a befogó-tételből D’O merőleges AD-re.
Ezekből következik, hogy O a két alapkör metszéspontja.
|
| Előzmény: [1260] HoA, 2009-08-27 14:53:48 |
|
| [1260] HoA | 2009-08-27 14:53:48 |
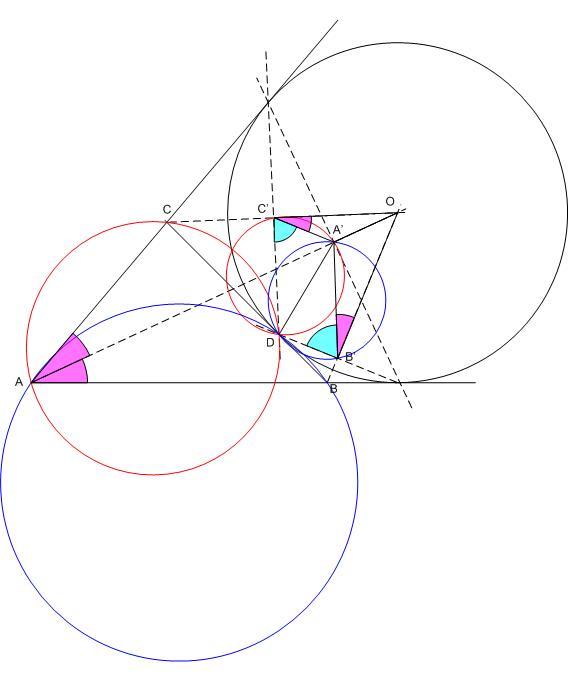
 Lassan bár, de haladunk a 151. feladat inverziót használó megoldásának teljes megadása felé. A 154. feladatra történő hivatkozást egyelőre fogadjuk el – később visszatérünk rá. AO Thálesz-körének bevetése nagyon tetszik. A 155. feladat megoldását alkalmazva készen is vagyunk. Mivel ez utóbbi eddig nem szerepelt, álljon itt egy elemi megoldás:
OA’ * OA = OB’ *OB, így OAB és OA’B’ háromszögek hasonlóak, OB’A’ = = /2 . Hasonlóan OC’A’ /2 . Hasonlóan OC’A’ = = /2. [1258] alapján OB’D /2. [1258] alapján OB’D =OC’D =OC’D =90o , A’B’D =90o , A’B’D =A’C’D =A’C’D , A’B’D és A’C’D körben a közös A’D húrhoz ugyanakkora kerületi szög tartozik, a két kör sugara egyenlő. , A’B’D és A’C’D körben a közös A’D húrhoz ugyanakkora kerületi szög tartozik, a két kör sugara egyenlő.
És most vissza a 154. feladatra. [1252] valóban hagyott gondolkodnivalót. A 154/a feladathoz nézzük [1253] ábráját. Legyen BAC = = , B’DB , B’DB = = , ekkor a BCC’B’ négyszögben AO és DO merőlegessége miatt B-nél 90o- , ekkor a BCC’B’ négyszögben AO és DO merőlegessége miatt B-nél 90o- /2- /2- /2 , C’-nél 90o+ /2 , C’-nél 90o+ /2+ /2+ /2 szög van, BCC’B’ húrnégyszög. /2 szög van, BCC’B’ húrnégyszög.
Az A illetve D középpontú megfelelő inverzió léte világos.
A következő bekezdés is teljes odáig, hogy – kis javítással - DB*DC=DB’*DC’=DA*DD’ . Az viszont, hogy ezért D’ = A’, nem adódik közvetlenül, hiszen az IA-ról leírtakat ID-re alkalmazva csak azt kapjuk, hogy A’ rajta van a DBB’ körön. Ahhoz, hogy belássuk, a DBB’ kör ugyanabban a pontban metszi AD-t mint az ABC kör, vagy hivatkoznunk kell a négy háromszög tételére ( DBB’ áthalad ABC és AB’C’ körök metszéspontján ) , vagy kitűzhetjük és megoldhatjuk a 154/c feladatot:
Ha a BCC’B’ húrnégyszög BB’ és CC’ oldalegyenesei A-ban, BC és B’C’ oldalegyenesei D-ben metszik egymást, akkor ABC és DB’B háromszögek körülírt köreinek ( B-től különböző ) M metszéspontja az AD egyenesen van.
Elfogadva tehát, hogy A’ = D’, tűzzük ki általánosan és oldjuk meg a 154/b feladatot: Adott az O1 középpontú I1 és az O2 középpontú I2 inverzió. Bizonyítsuk be, hogy ha I1-nél O2 képe megegyezik I2-nél O1 képével (P), akkor I1 és I2 alapköre merőleges.
Bizonyítás: Tekintsük O1O2 Thálesz-körének és az O1O2-re P-ben emelt merőlegesnek (egyik) Q metszéspontját. O1PQésO1QO2 derékszögű háromszögek hasonlóságából O1P.O1O2=O1Q2 , O1Q tehát I1 alapkörének sugara, Q rajta van I1 alapkörén. Hasonlóan adódik, hogy Q rajta van I2 alapkörén is. A Thálesz-kör miatt a Q-ból az alapkörök középpontjaiba húzott sugarak merőlegesek, így a két alapkör is merőleges.
Visszatérve az eredeti feladatra, a következő állítás „Ez viszont csak úgy lehet, ha az alapkörök átmennek O-n” közvetlenül nem adódik az előzőekből, csak az, hogy az alapkörök átmennek az inverzió középpontok Thálesz-körének egy közös pontján. Így kitűzhető a – 151-et közvetlenül nem támogató –
154/d feladat: Biz. : A 154/c feladat M pontjában az AD-re emelt merőleges áthalad a BCC’B’ húrnégyszög körülírt körének középpontján,
valamint a 151 megoldását előrevivő 154/e feladat: Ha a 154/c feladatban BCC’B’ egyúttal érintőnégyszög is, akkor az M pontban az AD-re emelt merőleges áthalad a BCC’B’ négyszög beírt körének középpontján .
Annak reményében, hogy lesz hozzászóló, majd innen folytatom.
|
 |
| Előzmény: [1259] BohnerGéza, 2009-08-18 20:47:01 |
|






 /2 szög alatt látszik. Így ANM
/2 szög alatt látszik. Így ANM =AB1M
=AB1M


 és k1 merőlegesen metszik"
és k1 merőlegesen metszik" 
 . Az AA1 szögfelező felezi a 2
. Az AA1 szögfelező felezi a 2




 , ekkor a BCC’B’ négyszögben AO és DO merőlegessége miatt B-nél 90o-
, ekkor a BCC’B’ négyszögben AO és DO merőlegessége miatt B-nél 90o-