| [1345] HoA | 2010-01-05 21:15:15 |
 Nem tudom, nem számoltam végig. Ha a [1341]-ben leírtakat saját magad találtad ki, nyilván tudod, miért. Ha mástól vetted át, akkor dolgozz egy kicsit: bizonyítsd vagy cáfold [1343] utolsó képletét.
|
| Előzmény: [1344] Tym0, 2010-01-05 20:26:30 |
|
| [1344] Tym0 | 2010-01-05 20:26:30 |
 Na most megint jól bekavartál. CSak annyit mondj hogy jó az amit az 1341-es hozzászólásomban írtam. Úgy kijön az általam keresett megoldás?
|
| Előzmény: [1343] HoA, 2010-01-05 19:55:45 |
|
| [1343] HoA | 2010-01-05 19:55:45 |
 Ismert, hogy a háromszög körülírt körének K középppontját a csúcsokból álló pontrendszer súlypontjaként úgy tudjuk előállítani, hogy a csúcsokat a megfelelő szögek kétszeresének sinusával súlyozzuk. Lásd pl. Reiman István: Geometria és határterületei:
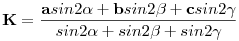
[1341]-ben a1,a2,a3 a (sík)háromszög oldalhosszainak négyzetei, a b1,b2,b3 súlyok a háromszög oldalait hagyományosan a,b,c-vel jelölve az
a2(b2+c2–a2),b2(c2+a2–b2),c2(a2+b2–c2)
mennyiségek. x,y,z a csúcsok ilyen súlyokkal vett súlypontjának koordinátái. Az nem baj, hogy a súlyok összege nem 1, és így a súlypont nincs a háromszög síkjában, mert az utolsó képlettel úgyis a gömbre vetíted. A megoldás akkor helyes, ha be tudod bizonyítani, hogy a súlyok aránya megfelelő, vagyis például
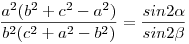
|
| Előzmény: [1341] Tym0, 2010-01-05 18:27:01 |
|
| [1342] laci777 | 2010-01-05 19:41:20 |
 Sziasztok, és b.ú.é.k. mindenkinek!
A Geometriai feladatok gyűjteménye I. 2776-os feladata sajnos megfogott. Tudna valaki segíteni benne? A feladat: Adott R sugarú gömbk köré írjunk olyan egyenes körkúpot, hogy térfogatának és a gömb térfogatának aránya adott k legyen. Határozzuk meg a kúp alapkörének a sugarát (r-t).
Addig jutottam, hogy r négyzet*m = 4*R köb*k (azaz gyakorlatilag semeddig), de a körkúp magassága (m), alkotója és sugara kívánatos aránya már kifogott rajtam.
Minden segtséget előre is köszönök! Sziasztok: Laci
|
|
| [1341] Tym0 | 2010-01-05 18:27:01 |
 Ehhez mit szóltok? Vagy ez ugyanaz amit ti mondtatok? Szerintem ez jó lesz. Szerintetek?
A gömb középpontja legyen az origó, a gömb sugara legyen R.
A kiindulási pontok a gömbön legyenek (x1,y1,z1), (x2,y2,z2), (x3,y3,z3).
Sorra számold ki az alábbi mennyiségeket:
a1 := (x2-x3)2 + (y2-y3)2 + (z2-z3)2
a2 := (x3-x1)2 + (y3-y1)2 + (z3-z1)2
a3 := (x1-x2)2 + (y1-y2)2 + (z1-z2)2
b1 := a1*(a2+a3-a1)
b2 := a2*(a3+a1-a2)
b3 := a3*(a1+a2-a3)
x := b1*x1 + b2*x2 + b3*x3
y := b1*y1 + b2*y2 + b3*y3
z := b1*z1 + b2*z2 + b3*z3
c : = R/gyök(x2+y2+z2)
A gömbön a körülírt kör középpontjának keresett koordinátái (c*x,c*y,c*z).
|
| Előzmény: [1340] HoA, 2010-01-05 11:40:36 |
|
| [1340] HoA | 2010-01-05 11:40:36 |
 Az eddigiek alapján a lépések:
-Adottak A, B, és C földrajzi koordinátái, északi szélesség =  , keleti hosszúság = , keleti hosszúság = 
-Átszámítjuk Descartes-koordinátákba : Pz=sin ;Px=cos ;Px=cos ,Py=sin ,Py=sin ( P = A,B,C ) ( P = A,B,C )
-Válasszuk úgy a jelölést, hogy ABC pozitív körüljárású  legyen legyen
-Képezzük az N = (B-A) x (C-A) vektorszorzatot, ez a gömb középpontjából kifelé mutat.
-A keresett középpont földrajzi koordonátáit az előzőek alapján kapjuk: sin  =Nz/|N| , tg =Nz/|N| , tg  =Ny/Nx =Ny/Nx
|
| Előzmény: [1334] Tym0, 2010-01-04 22:31:59 |
|
| [1339] HoA | 2010-01-05 11:14:08 |
 „Mindenkinek” igaza van, függetlenül attól, hogy gömbi vagy Descartes koordinátákat használunk.
-a gömb 3 különböző pontja, mint 3 térbeli pont, meghatároz egy S síkot
-ez a sík a gömböt egy körben metszi, és mivel a 3 pont a síkon is és a gömbön is rajta van, ez a kör éppen a 3 pont által meghatározott háromszög körülírt köre
-A BohnerGéza által javasolt vektorszorzat S (egy) N normálvektora, tehát S-re merőleges.
-A gömb középpontjából a gömböt metsző S síkra bocsátott N merőleges S –et a gömb és S metszésvonalát képező kör középpontjában döfi ( szimmetria ) . Talán ez hiányzott a leírtakhoz.
-N a gömböt abban a pontban metszi, amelyik egyenlő távolságra van a 3 adott ponttól – a földgömbnek ebbe a ponjába beszúrt körzővel a 3 ponton áthaladó kört lehet rajzolni
-A körközéppont földrajzi koordinátáinak meghatározásához N hossza lényegtelen. A Descartes koordinátáknak csak itt van szerepe. Ha a földrajzi szélességet  -vel, a hosszúságot -vel, a hosszúságot  –val jelöljük, akkor sin –val jelöljük, akkor sin  =Nz/|N| , tg =Nz/|N| , tg  =Ny/Nx =Ny/Nx
|
| Előzmény: [1338] sakkmath, 2010-01-05 09:59:14 |
|
| [1338] sakkmath | 2010-01-05 09:59:14 |
 Szerintem Jonasnak (1328) igaza van akkor, ha a gömbháromszög csúcsai euklideszi koordinátákkal adottak.
Ha viszont az adott koordináták gömbi, földrajzi koordináták, akkor az eddigi hozzászólások nem érvényesek, ugyanis a többi hozzászóló is euklideszi koordinátarendszerben gondolkodott.
|
| Előzmény: [1336] Tym0, 2010-01-05 01:38:08 |
|
|
| [1336] Tym0 | 2010-01-05 01:38:08 |
 Ez mind oké. De foylton síkot említesz. Egy gömfelületen levő háromszög nem lehet sík hiszen a gömbnek a felületén van. Vagy én vagyok a hülye és én nem értem...
|
| Előzmény: [1335] BohnerGéza, 2010-01-04 23:08:22 |
|
|
| [1334] Tym0 | 2010-01-04 22:31:59 |
 A lépéseket próbáld meg leírni lécci. Most ott tartok hogy van 3 (a háromszög csúcspontjai) + 3 (a háromszög oldalainak felezőpontjai) koordinátapontom (amik ugye x,y,z koordináták mert térről beszélünk). És ugye a göm középpontjának koordinátja ami ugye x,y,z alakban 0,0,0. Ezután mi jön? Mik a lépések?
|
|
|
| [1332] BohnerGéza | 2010-01-04 21:14:01 |
 Mivel egyforma húrokhoz egyforma gömbi távolságok tartoznak:
Térben a három ponttól egyenlő távolságra lévő pontok halmaza: a háromszög körülírt körének középpontjában a síkjára állított merőleges. Esesükben ezen rajta van az eredeti gömb középpontja is.
Tehát keressük a körülírt kör kp-ján és a gömb kp-ján átmenő egyenesnek és a gömbnek a megfelelő oldalon lévő metszéspontját.
(Ha nem elég, folytatom.)
|
| Előzmény: [1329] Tym0, 2010-01-04 20:40:33 |
|
| [1331] Tym0 | 2010-01-04 21:09:49 |
 kicsit érthetőbben? Mert ez nekem magas
|
|
|
| [1329] Tym0 | 2010-01-04 20:40:33 |
 Dehogy ugyanaz. Mert másképp viselkedik. A gömb az egy térbeli alakzat nem síkbeli és nem euklidészi közegben van vagy valami ilyesmi... Amúgy azon már túl vagyok... És nem lett jó
|
|
| [1328] jonas | 2010-01-04 20:26:08 |
 Szerintem számold ki a három csúcs által alkotott síkháromszög köréírt körét, mert az ugyanaz, mint ha gömbháromszögként veszed a köréírt kört.
|
| Előzmény: [1327] Tym0, 2010-01-04 17:05:04 |
|
| [1327] Tym0 | 2010-01-04 17:05:04 |
 Sziasztok!
Egy kis segítséget szeretnék kérni gömbi geometria témakörben!
A problémám a következő:
Kiváncsi vagyok egy gömbháromszög köré írható kör középpontjának koordinátáira, úgy hogy csak a háromszög csúcsainak koordinátái vannak megadva.
Tehát annak a pontnak a koordinátáira, ami a gömbháromszög mindhárom csúcsától egyenlő távolságra van.
Konkrétan: Van három földrajzi koordinátám (századszögmásodperces pontossággal megadva) nem túl nagy távolságra egymástól kb 200km-re. (Mindhárom É.sz. és K.h.) És kiváncsi vagyok annak a pontnak a koordináira, ami mindhárom ponttól egyenlő távolságra van.
Addig már eljutottam hogy a földrajzi koordinátákat átváltottam ekvatoriális, azaz gömbi koordinátákká. És a háromszög mindhárom oldalának felezőpontjai is megvannak. Itt akadtam el...
Arra gondoltam hogy elég valamely két oldal felezőmerőleges gömbi főkörének metszéspontjának koordinátáit kiszámolni. De hogyan??????????????
Ja és vigyázni kell, mert a gömbi főkörök két pontban metszik egymást, azok közül csak az egyik lesz jó mert a másik a gömb átellenes pontján van.
Valaki tudna nekem segíteni????????
|
|
| [1326] HoA | 2010-01-03 20:41:42 |
 Mivel kedvenc vesszőparipámat, az egységsugarú körbe írt szabályos 18-szög tulajdonságait érinti, B.4221 elemi megoldását feltettem http://www.komal.hu/forum/forum.cgi?a=to&tid=26&tc=500 -ba ( Lejárt határidejű KÖMAL feladatokról )
|
|
| [1325] BohnerGéza | 2009-12-02 22:57:49 |
 HoA! Szép!
Ennek a feladatnak egy sok számolásos megoldásáról hallottam, sajnos nem láttam. Az inverzióval átalakított feladatot azért írtam, hátha sikerül egy, az utolsó mondatodnak megfelelő, megoldás összehozni. (Nem adtam föl.)
|
| Előzmény: [1324] HoA, 2009-12-02 21:15:22 |
|
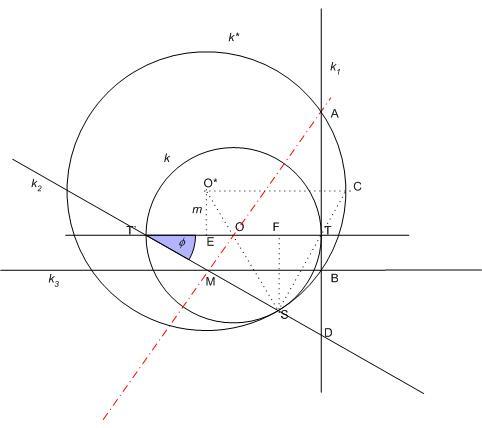
| [1324] HoA | 2009-12-02 21:15:22 |
 Az egység sugarú k körön jellemezzük S helyzetét az ST’T =  szöggel. k* sugara legyen r. Az AB ív felezőpntja C, k1 és k2 metszéspontja D, k* középpontja O*, O* és S merőleges vetülete TT’ –re E illetve F, végül k2 és k3 metszéspontja M. A akkor és csak akkor van az MO egyenesen, ha az ATO és ABM derékszögű háromszögek hasonlók, vagyis ha szöggel. k* sugara legyen r. Az AB ív felezőpntja C, k1 és k2 metszéspontja D, k* középpontja O*, O* és S merőleges vetülete TT’ –re E illetve F, végül k2 és k3 metszéspontja M. A akkor és csak akkor van az MO egyenesen, ha az ATO és ABM derékszögű háromszögek hasonlók, vagyis ha 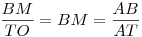 . S a k és k* körök hasonlósági középpontja, így O*O=r-1 és CT=(r-1)TS . T’S=2cos . S a k és k* körök hasonlósági középpontja, így O*O=r-1 és CT=(r-1)TS . T’S=2cos , SF=2cos , SF=2cos sin sin és így O*E=m=2cos és így O*E=m=2cos sin sin (r-1) . Legyen az AB húr hossza 2h . (r-1) . Legyen az AB húr hossza 2h . 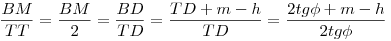 , , 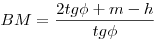 Erről kell belátni, hogy megegyezik Erről kell belátni, hogy megegyezik 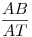 -vel, vagyis -vel, vagyis 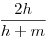 -mel. Felhasználjuk, hogy a szelőtétel értelmében AT.TB=CT.TS , (h+m)(h-m)=2sin -mel. Felhasználjuk, hogy a szelőtétel értelmében AT.TB=CT.TS , (h+m)(h-m)=2sin .(r-1)2sin .(r-1)2sin =4(r-1)sin2 =4(r-1)sin2 . . 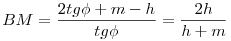 , (2tg , (2tg +m–h)(h+m)=2h.tg +m–h)(h+m)=2h.tg =2tg =2tg (h+m)–(h-m)(h+m)=2h.tg (h+m)–(h-m)(h+m)=2h.tg +2mtg +2mtg -(h-m)(h+m) . 2mtg -(h-m)(h+m) . 2mtg =(h-m)(h+m) A baloldal 2mtg =(h-m)(h+m) A baloldal 2mtg =4cos =4cos sin sin (r-1)tg (r-1)tg =4(r-1)sin2 =4(r-1)sin2 , a feltétel teljesül. , a feltétel teljesül.
Jó lenne egy szemléletesebb megoldás, esetleg az inverzió előtti feladatra is.
|
 |
| Előzmény: [1315] BohnerGéza, 2009-11-24 21:26:53 |
|
| [1323] HoA | 2009-11-30 15:29:28 |
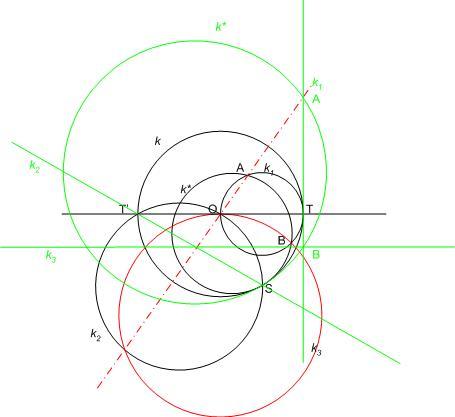
 A kör középpontján áthaladó körökkel és egyenesekkel a feladat nagyon inverzió szagú. Megadom az inverzióval keletkező feladatot és ábráját (zöld vonalak) , mert a megoldás így sem triviális.
Jelöljük k-val az O középpontú, az S és T ponton átmenő kört, T’-vel a T-ből induló átmérő másik végét. Legyen k1 k T-beli érintője, k2 az ST' egyenes. Jelöljön k* egy k-t magába foglaló és S-ben érintő kört. k* és k1 metszéspontjai legyenek A és B. Legyen k3 a B-n átmenő TT'-vel párhuzamos egyenes. Bizonyítandó, hogy a k2 és k3 metszéspontján valamint O-n áthaladó egyenes tartalmazza A-t.
|
 |
| Előzmény: [1315] BohnerGéza, 2009-11-24 21:26:53 |
|
|
|




 , keleti hosszúság =
, keleti hosszúság = 
 legyen
legyen