| [146] Hajba Károly | 2004-06-10 13:27:05 |
 Kedves Csimby!
Gratulálok, szép munkát végeztél. Írj erről egy nagyobb cikket, s beszéld rá Gézát, hogy tegye be a lapba. Így publikálva lesz, Tied az elsőség, ha más még nem foglalkozatt vele. :o)
Illetve fordítsd le angolra is és jelezz Eriknek.
Én akkor februárban foglalkoztam egy kicsit vele, de az elméleti hátterével nem. Habár Grafok vannak a családomban, a matematika eme területén csak kissé vagyok jártas. :o) Készítettem egy 60 elemes napsugaras változatot ill. papíron kerestem a 6 és 8 elemes változatot. Most már tudom, miért eredménytelenül. :o)
Vannak olyan problémafelvetések, melyek a felvetőnek nagyon érdekes, de mást vagy nem érdekel vagy nem ért annyira hozzá, így elsikkad. Nekem ilyen az egységnégyzet 11 egy kisebb négyzetre történő osztása, azaz hányféleképpen lehet felosztani 11 kisnégyzetre. Többször felvetettem, de senki nem reagált rá. Erre mondja a francia: C'est la vie!
Üdv: HK
|
| Előzmény: [145] Csimby, 2004-06-10 03:04:46 |
|
| [145] Csimby | 2004-06-10 03:04:46 |
 A 15. feladatra (65. hozzászólás) senki sem reagált, pedig szerintem érdekes problémakör. Akit mégis érdekelne a megoldás, csináltam egy honlapot ahol elég sok eredmény fenn van. Van amit elbonyolítottam és van amit nem bizonyítottam, tehát ha valakinek bármi észrevétele van, írjon. Mégegyszer a feladat: Milyen n esetén lehet n db. egybevágó négyzetet úgy elhelyezni a síkban, hogy mindegyik pontosan 3 másikat érintsen és az alakzat összefüggő legyen (érintésnek tekintjük azt is amikor a négyzetek csak egy pontban érintkeznek).
|
|
| [144] BohnerGéza | 2004-06-08 14:13:29 |
 Két ötlet a 34. feladat megoldásához:
1. Tekintsük a BCD körülírt körét, igazoljuk hogy e-vel való metszéspontja E! (Ebben az esetben van értelme a D ne lehessen C feltételnek, ennek hiányában ezt az esetet külön kellene vizsgálni. A második esetben nem kell a feltétel.)
2. Forgassunk B körül –60 fokkal! AC képe e lesz, így D képe e-re esik, igazoljuk, hogy ez E!
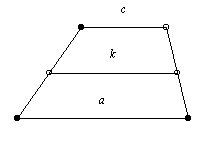
A 33. feladat megoldását mindenkinek javaslom (akár 7. osztályos kortól), aki tud a trapéz középvonaláról: a középvonal a párhuzamos oldalak számtani közepe. (2k=a+c)
|
 |
|
| [143] BohnerGéza | 2004-06-01 14:06:25 |
 A [46]-ban kitűzött 14. feladat egy megoldása: Tudjuk, hogy AB || CD és AX || CY, bizonyítadó, DX || YB. Jelölje a szárak metszéspontját P! A párh. szelők tételéből és megfordításából következik:
Tudjuk: (1.) PD/PA=PC/PB (2.) PA/PY=PX/PC.
Elég: PD/PY=PX/PB, amit (1.) és (2.) megfelelő oldalainak összeszorzásával meg is kapunk.
Megjegyzés: A [46]-ban kitűzött feladat megoldása szerepelt a [57], [62] és [mostani - kb. 3] hozzászólásokban, érdemes mindegyikkel foglalkozni.
|
|
| [142] lorantfy | 2004-05-19 16:51:28 |
 Kedves Géza!
Kösz a megoldást! Pontosan így gondoltam. Ha már hozzászólok beírok egy egyszerű kis példát is:
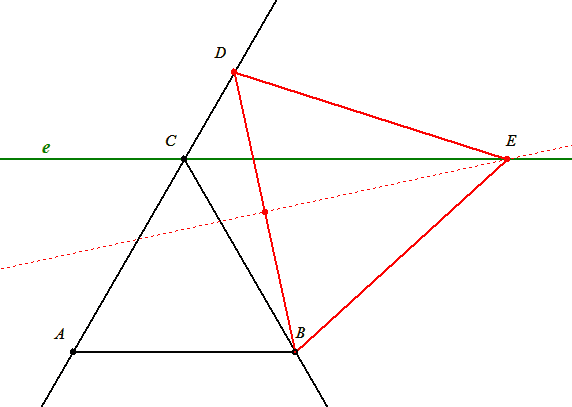
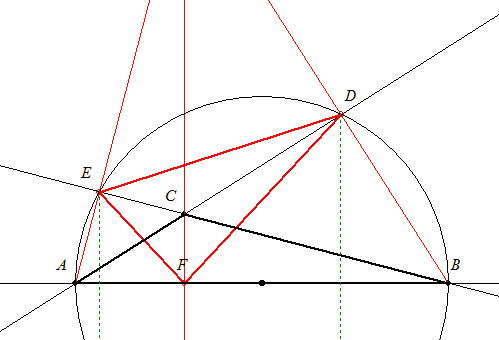
34. feladat: ABC egyenlő oldalú  C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE  is szabályos! is szabályos!
|
 |
| Előzmény: [141] BohnerGéza, 2004-05-18 21:52:48 |
|
| [141] BohnerGéza | 2004-05-18 21:52:48 |
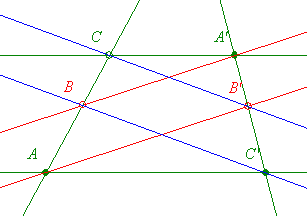
 A 14. feladat egy megoldása: Eredetileg így szól: (ne kelljen most megkeresni!) Vegyük fel az ABCD trapéz AD szárán az X, BC szárán az Y pontot. Bbh. ha AY párhuzamos CX egyenessel, akkor DY is párhuzamos BX egyenessel!
Alkalmazzuk a Pappos-tételt, mely például szerepel a [137]-es hozzászólásban. Használjuk ennek jelöléseit! Tehát az eredeti A legyen A, B-->C’, C-->A’, D-->C, X-->B és Y-->B’! Tudjuk, hogy AC’ és A’C valamint AB’ és A’B metszéspontja az ideális egyenesen van, a BC’ és C’B is ott kell messe egymást, tehát párhuzamossak.
|
 |
| Előzmény: [46] lorantfy, 2004-02-07 00:15:18 |
|
| [140] BohnerGéza | 2004-05-17 14:20:00 |
 Mivel igen leállt most a fórum: A 32. feladatról:
A feladatot a http://matek.fazekas.hu/portal/kutatomunkak/Feuerbach/index.html cikkből vettem. Érdemes tanulmányozni az ottani megoldást (és az egész hónlapot), de sokkal „szebbet” is lehet találni. A 32. b) feladathoz: Ha beírt kör szerepel egy feladatban, mindig érdemes lehet a hozzáírt körrel kapcsolatban az analógiát keresni ( és az Euklidesszel ellenőrizni a sejtést).
A [62.] hozzászólásban megígértem, hogy a [46] 14. feladatára adok ( a kitűzőnek tetsző ) megoldást. Mivel eddig más ezt nem tette meg, nekiállok.
|
|
| [139] lorantfy | 2004-05-09 15:12:01 |
 Kedves Géza és Fórumosok!
Bár a 30-31-es feladatot még nem oldottam meg, de tanulmányozása során találtam egy egyszerűen bizonyítható állítást:
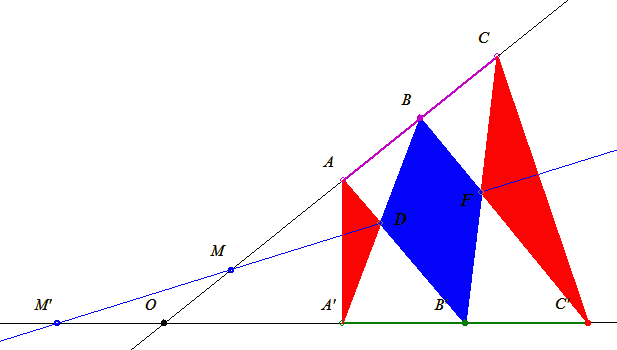
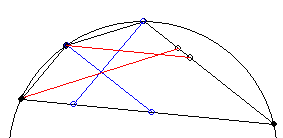
33. feladat: Legyen két egymást O-ban metsző f és f’ egyenesünk egyikén az A, B és C pont, másikán az A’, B’ és C’. Legyen AB' és BA' metszéspontja D, BC' és CB' metszéspontja pedig F. Ha AB=BC és A’B’=B’C’ akkor
TAA'D+TCC'F=TBDB'F
|
 |
| Előzmény: [137] BohnerGéza, 2004-04-30 14:07:27 |
|
| [138] BohnerGéza | 2004-05-04 12:58:42 |
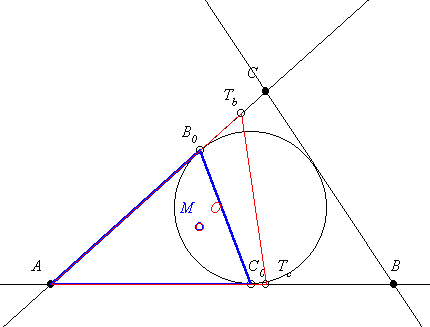
 32. feladat: Az ABC háromszögben a beírt kör érintési pontjai, ill. a magasságok talppontjai az AB ill. AC oldalon Co és Tc ill. Bo és Tb. Legyen M az ACoBo magasságpontja és O az ATcTb beírt körének középpontja. Igazoljuk, hogy O és M egybeesik.
32. b) feladat: Mondjuk ki és igazoljuk a 32. feladatnak megfelelő (analóg) feladatot.
A 31. b) feladat megoldásához: vektorok segítségével megy, ha jól választjuk meg az indulást, nem is túl sok számolás. Nagy örömmel látnék nem vektoros és nem koordinátageometriai megoldást is. Tanulnék belőle, mert egyelőre nem tudom, hogy kezdjek neki!
|
 |
|
| [137] BohnerGéza | 2004-04-30 14:07:27 |
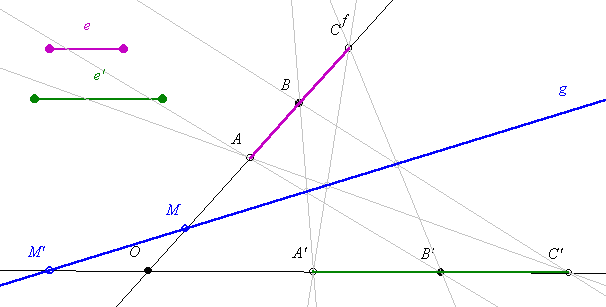
 A [128]-as hozzászólásában László felvetett egy problémát, amellyel érdemes foglalkozni. Legyen két egymást O-ban metsző f és f’ egyenesünk egyikén az A, B és C pont, másikán az A’, B’ és C’. Papposz tétele szerint az AB’ és A’B, az AC’ és A’C valamint a BC’ és B’C által meghatározott metszéspontok egy egyenesen vannak, jelöljük ezt g-vel. László fölveti a következőt:
30. a) feladat: Ha AB=BC=A’B’=B’C’, akkor g párhuzamos a két egyenes szögfelezőjével.
Egyenértékű ezzel a következő állítás: 30. b) feladat: Ha valamelyik ponthármast (pl. A-t B-t és C-t) az egyenesén a fenti feltételt tartva mozgatjuk, akkor a „g”-k párhuzamosak lesznek.
Az előző feladatok általánosítása a következő:
31. a) feladat: Ha AB=BC=e és A’B’=B’C’=e’, akkor ha valamelyik ponthármast (pl. A-t B-t és C-t) az egyenesén a feltételt tartva mozgatjuk, akkor a „g”-k párhuzamosak lesznek.
31. b) feladat: Ha g f-et egy M-ben f’-t egy M’-ben metszi, akkor OM:OM’=e:e’, valamint g csakkor halad át O-n, ha OB:OB’=e:e’.
Bocs, minden feladat akkor lesz az, ha hozzátesszük, hogy bizonyítandó!
|
 |
| Előzmény: [128] lorantfy, 2004-04-27 14:19:02 |
|
| [136] lorantfy | 2004-04-29 23:43:15 |
 Kedves NádorP, Géza és Fórumosok!
Jogos volt Géza bírálata, [131]-ben mindenütt "<" jeleket kellett volna írnom. "Lehet látni", hogy  növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet. növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet.
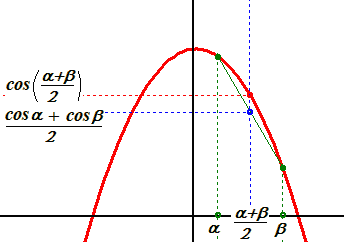
A szintén ott említett Jensen egyenlőtlenséghez már akkor fel akartam tenni egy ábrát, most megteszem, mert itt is előjön. ( Ha jól megnézitek, látható, hogy ez nem cos fgv. hanem egy parabola. Bocs! Euklidesben ezt egyszerűbb rajzolni.)
|
 |
| Előzmény: [135] nadorp, 2004-04-29 16:25:58 |
|
|
| [134] Hajba Károly | 2004-04-27 23:04:03 |
 Kedves Géza és László!
Én is közreadom a megoldásomat a 28. feladatra:
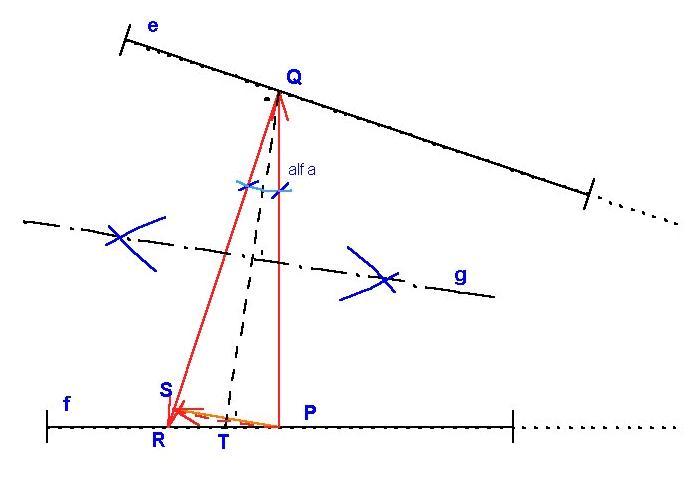
Az f szakasz tetszőleges P pontjára állított merőleges Q-t metszi ki e-ből. Erre a pontra állított merőleges pedig R-t metszi ki f-ből. P-t Q körül a QR szakaszra forgatva kimetszi S-t. Q-ból PS-re bocsátott merőleges T-t metszi ki f-ből. PQS egyenlő szárű háromszög hasonló TOQ egyenlő szárű háromszög hasonló TOQ -gel és egymásra merőlegesek, ahol O az e és f szakaszok meghosszabbításának metszéspontja. Így a QT szakaszfelező merőlegese átmegy O-n, azaz a kivánt szakaszfelező. -gel és egymásra merőlegesek, ahol O az e és f szakaszok meghosszabbításának metszéspontja. Így a QT szakaszfelező merőlegese átmegy O-n, azaz a kivánt szakaszfelező.
Direkt szakaszokat írtam, ezzel is példázva, hogy nem kell O-t felhasználni.
HK
|
 |
| Előzmény: [130] lorantfy, 2004-04-27 18:31:12 |
|
| [133] BohnerGéza | 2004-04-27 22:11:46 |
 Kedves László!
Kicsit fáradt vagyok, különben az előző hozzászólásomban a megszólításra és a megoldásod fölösleges bírálatára is jobban figyeltem volna, hiszen semmi baj nincs vele, nyugodtan elhagyható az egyenlőség.
|
| Előzmény: [132] BohnerGéza, 2004-04-27 21:58:46 |
|
| [132] BohnerGéza | 2004-04-27 21:58:46 |
 Kedves Laci és Fórumosok!
Az Euklideszben az index beírása A&1 formában lehetséges.
Nagyon szép és tanulságos a 29. feladatra írt megoldásod. Kicsit szépséghibája, hogy az egyenlőséget nem megengedve is igaz. Ha a területek 0-hoz tartanak lesz az arány határértéke kettő. Érdemes lehet a feladatot megfogalmazni a következő általánosabb formában: Egy talpponti háromszög és az eredeti háromszög területének arányát tekintsük negatívnak, ha a háromszög tompaszögű. ekkor igaz a -2<arány<=1/4.
|
| Előzmény: [131] lorantfy, 2004-04-27 21:13:37 |
|
|
| [130] lorantfy | 2004-04-27 18:31:12 |
 Kedves Géza!
Jó ez a szögfelezős megoldás és egyszerűbb is mint az enyém.
Azt szeretném kérdezni, hogy az indexelt pont megjelölést az Euklidesben hogy csinálod? (pl A1). Lehet, hogy csak az újabb verzió engedi meg? (Enyém 2.02.)
|
 |
| Előzmény: [129] BohnerGéza, 2004-04-27 14:46:47 |
|
| [129] BohnerGéza | 2004-04-27 14:46:47 |
 29. feladat: ( A [123] hozzászólás 28. feladata. )Igazoljuk, hogy tompaszögű háromszögben a talpponti és eredeti háromszög területének aránya kettőnél kisebb, nem negatív érték!
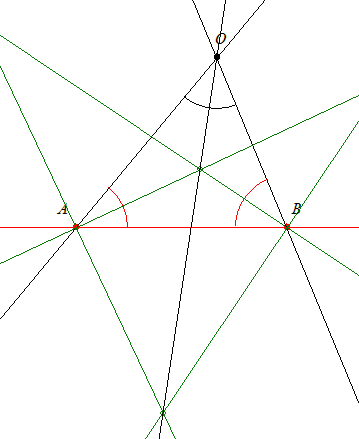
[125] 28. feladatának megoldása: Legyen a két nem párhuzamos egyenes metszéspontja O, a két egyenes további egy-egy pontja A ill. B. Az OAB háromszög A-nál és B-nél lévő külső szögfelezőivel szerkeszthető az O-nál lévő belső egy pontja. Hasonlóan kapjuk egy másik pontját is.
|
| Előzmény: [125] Hajba Károly, 2004-04-27 12:18:39 |
|
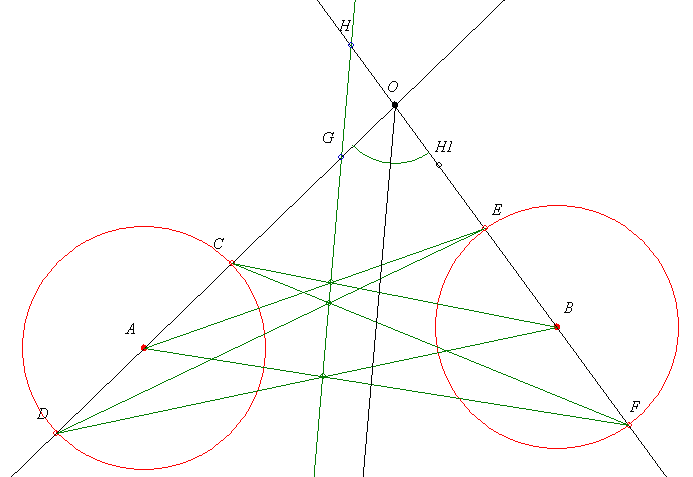
| [128] lorantfy | 2004-04-27 14:19:02 |
 28. megoldás vázlat: Használjuk a Papposz tételt. Vegyünk fel a szögszárakon tetszőleges A és B pontot. Ezekből ugyanazzal a sugárral körözve kapjuk a szögszárakon a C,D és E,F pontokat. Szóval felveszünk a szögszárakon 3-3 pontot azonos távolságokkal. A megfelelő metszéspontokat összekötve ezek egy egyenesen lesznek, mondja Papposz. Mivel a szakaszok egyenlőek ez az egyenes párhuzamos a szögfelezővel, gondolom én. (A bizonyítást másra hagyom!). A szögszárakból kimetszett G,H pontokból a szögfelező megszerkeszthető a egyenesek metszéspontjának felhasználása nélkül.
|
 |
| Előzmény: [125] Hajba Károly, 2004-04-27 12:18:39 |
|
|
|
| [125] Hajba Károly | 2004-04-27 12:18:39 |
 28. feladat:
Szerkesszük meg két nem párhuzamos egyenes szögfelező(jé/i)t a metszéspont felhasználása nélkül!
HK
|
|
|
| [123] BohnerGéza | 2004-04-25 23:43:53 |
 A versenyfeladatok [15]-ben szereplő és a következő hozzászólásokban megoldott ott 6. feladattal kapcsolatban tűzöm ki az alábbit.
Ráadásul egy kis adalék az Euklideshez. Megnéztem vele, hogy mennyi lehet a talpponti és eredeti háromszög területének aránya.
A szorzásokat és az arányszámolást a párhuzamos szelők tételével szerkesztettem meg. Hegyesszögű háromszög esetén kijött a már megoldott 0<=arány<=1/4. A valószínű eredmény tompaszögűre 0<=arány<2.
28. feladat: Igazoljuk, hogy tompaszögű háromszögben a talpponti és eredeti háromszög területének aránya kettőnél kisebb, nem negatív érték!
|
|
| [122] lorantfy | 2004-04-25 19:13:17 |
 Kedves Géza és Fórumosok!
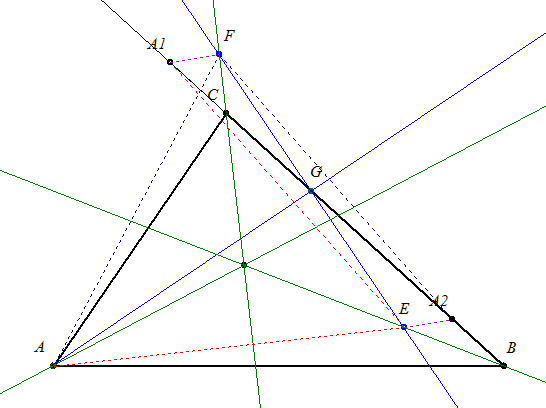
Nagyon szép a megoldás. Én is próbálkoztam tükrözéssel, de nem jött össze. Minthogy már kész az ábrám 22. megoldása alapján rögtön megvan a 20. feladat megoldása: Tükrözzük az A pontot a B-n és C-n átmenő belső szögfelezőkre. Így BA1=c és CA2=b.
G a beírt kör érintési pontja, tehát CG=s-c és BG=s-b. Ezekből A1G=c-(s-b)=c+b-s és A2G=b-(s-c)=b+c-s vagyis A1G=A2G. Létezik az A1EA2F paralelogramma, ahol E és F a szögfelezőkön lévő pontok és G felezi EF szakaszt. Ekkor a paralelogramma szemközti oldallai: A1E=FA2. A tükrözések miatt:
A1E=AE A2F=AF AE=AF AE=AF
AEF egyenlő szárú háromszögben EF merőleges AG-re.
|
 |
| Előzmény: [121] BohnerGéza, 2004-04-25 16:38:35 |
|







 C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE
C csúcsában húzzunk párhuzamost az AB oldallal, legyen ez e. Az AC oldal egyenesén vegyünk fel egy C-től különböző D pontot. BD szakasz felező merőlegese az e egyenest E-ben metszi. Bbh. BDE 




 növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet.
növekedésével az arány 2-höz tart, de az kevés! Nagyon elegáns NádorP bizonyítása. Akit érdekel a területeknél használt képlet a Versenyfeladatok témában NádorP [16] hozzászólásában utánna nézhet. 

 ,
, ,
,


 AE=AF
AE=AF