| [1615] w | 2012-12-12 17:59:04 |
 Ez is szép megoldás.
A feladat bemutatja, hogy több ismerettel sokkal bonyolultabban oldanánk meg egy nem nyilvánvaló általános iskolás feladatot, mint egy korlátos ismerettel rendelkező nyolcadikos. (Persze az más kérdés, hogy egy általános iskolás mit tesz, ha egy trigonometrikus egyenletet kellene fejtegetni.) Akinek elemi geometriával van dolga, annak állandó gyakorlásra van szüksége, hogy ezekhez való érzékét fenntartsa. (Megjegyzendő, hogy mindenhol van kivétel.)
A feladat megoldása:
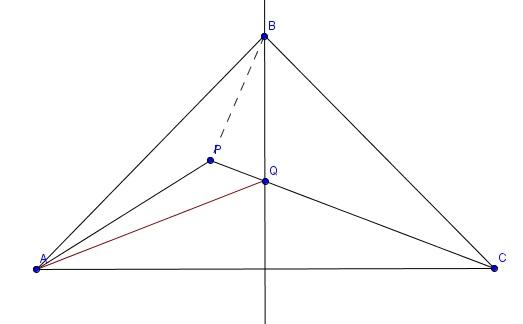
Célszerű az egyenlő szárúságot kihasználni. Rajzoljuk be a háromszög szimmetriatengelyét, ez messe CP-t Q-ban, ekkor QAC<=ACQ<=30°. Vegyük észre, hogy AP felezi a BAQ<-et, ráadásul PQ az AQB< felezője. Így P az AQB háromszög beírt körének középpontja, azaz BP felezi ABQ<-et. BPC<=180°-(80°/2+80°/4)-(50°-30°)=100°.
Ez egyszerű volt. Kis túlzással annyi kellett hozzá, hogy észrevesszük, hogy az egyenlő szárú háromszög szimmetrikus. Aki erre rákényszerítené a szabályos 18-szöget, az azért teszi, mert a feladatot ennél összetettebbnek képzeli, és jogosan. Tehát ajánlom a feladatok egyszerű megközelítését (aki elolvasta a bemutatkozásomat, az el is várhatja a könnyebb példákat :).
Megint más kérdés, hogy milyen a feladat általánosítása...
|
 |
| Előzmény: [1614] HoA, 2012-12-11 13:07:32 |
|
| [1614] HoA | 2012-12-11 13:07:32 |
 Hogy mennyire tömény és elegáns, azt ítélje meg más, minden esetre "nyolcadikosabb" , mint az előző.
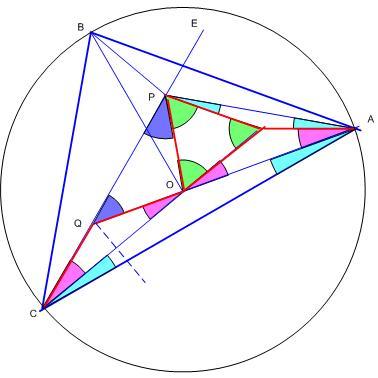
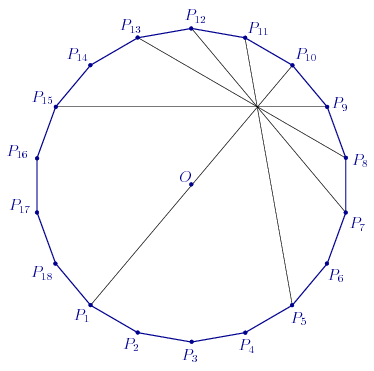
Építsük fel a mellékelt ábrát az ABC háromszög csúcsaiból, a körülírt kör O középpontjából és a CA oldallal 30 fokos szöget bezáró CE egyenesből kiindulva. CO felező merőlegesének és CE -nek a metszéspontja Q. Az állandó QC hosszúságú piros szakaszok ismételt felméregetésével kialakul az ábra. A 10, 20, 40 ill. 60 fokos szögeket kékkel, rózsaszínnel, lilával ill. zölddel jelöltem. Látható - és persze bizonyítható - , hogy P a feladatban definiált pont.
A BPC háromszöget O körül pozitív irányban 100 fokkal elforgatva P Q-ba , B C-be kerül, A BP szakasz képe tehát a PC-vel egy egyenesbe eső CQ, ezért BPC szög 100 fok.
|
 |
| Előzmény: [1611] w, 2012-12-10 16:46:48 |
|
| [1613] w | 2012-12-10 22:22:18 |
 Jogos a hozzászólásod. Én arra gondoltam, hogy a feladatot úgy is meg lehet oldani, hogy csak a következőket használhatjuk: háromszög belsőszög-összege, nevezetes vonalai, beírt kör, szög/szakasz/pont felvétele.
A Fálesz-HoA-megoldás sokkal hasznosabb, mint az, amire gondolok. Mindenesetre hamarosan - amint lesz időm az ábrát elkészíteni - közlöm a megoldásomat.
******
Mutassuk meg, hogy ha egy háromszög két belső szögfelezője azonos hosszú, akkor és csak akkor a háromszög egyenlő szárú.
|
| Előzmény: [1612] Lóczi Lajos, 2012-12-10 18:30:06 |
|
|
| [1611] w | 2012-12-10 16:46:48 |
 Köszönöm szépen, a megoldásotok nagyon szép, és igen sok feladatra felhasználható.
A feladatot eredetileg nyolcadik osztályosoknak tűzték ki, talán 2007-ben (?), ezért nyilván van olyan megoldás, ami tömény, elegáns háromszöggeometria.
|
| Előzmény: [1610] HoA, 2012-12-10 11:26:43 |
|
| [1610] HoA | 2012-12-10 11:26:43 |
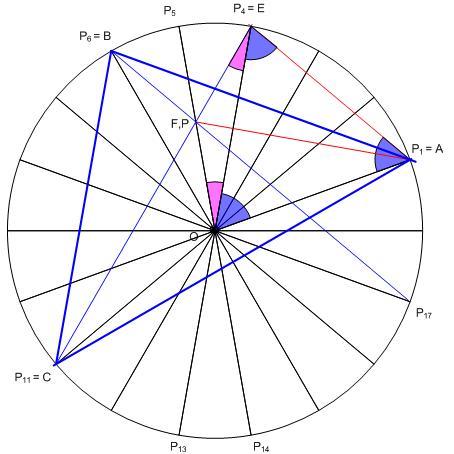
 A [1609] –beli megközelítés egy konkrét megvalósítása, a szükséges nem triviális közös metszéspont bizonyításával: Válasszuk meg az A, B, C csúcsokat az ábra szerint, így ABC a feladatban szereplő háromszög. Mivel egy sokszög oldalhoz, ill. a körülírt körben a hozzá tartozó ívhez 10 fokos kerületi és 20 fokos középponti szög tartozik, AOC  = 160 fok , így CAO = 160 fok , így CAO  = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF  = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE  = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO  = 30 fok, FAC = 30 fok, FAC  = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP  = P6CP4 = P6CP4 = 20 fok, CBP = 20 fok, CBP  = P11BP17 = P11BP17 = 60 fok, így BPC = 60 fok, így BPC  = 100 fok. = 100 fok.
|
 |
| Előzmény: [1609] Fálesz Mihály, 2012-12-10 09:28:23 |
|
| [1609] Fálesz Mihály | 2012-12-10 09:28:23 |
 Az ilyenfajta feladatokhoz egy kiváló cikk: Csirmaz László: Egy geometriai feladatról
A lényeg röviden:
1. Egy szabályos 18-szögben az átlók közötti szögek mind a 10o többszörösei.
2. Vannak olyan átlók, amik nem teljesen triviálisan egy ponton mennek át. Például a O középpontú P1P2...P18 szabályos 18-szögben a P9P15 átló az OP12 sugár felező merőlegese, és ebből következik, hogy a P1P10 egyenes tükörképe a P9P15 átlóra éppen a P7P12 egyenes. Ha ezeket a P1P10 átmérőre is tükrözzük, láthatjuk, hogy a P1P10, P5P11, P7P12. P8P13 és P9P15 átlók egy ponton mennek át.
3. A feladat megoldása ezek után abból áll, hogy megkeressük a rengeteg oldal és átló között a feladat ábráját...
|
 |
| Előzmény: [1608] w, 2012-12-09 11:22:59 |
|
|
|
| [1606] w | 2012-12-08 21:34:35 |
 ABC háromszögben AB=AC, P belső pontra PAC<=40 fok, ACP<=30 fok. Mekkora a BPC<, ha ABC<=80 fok?
|
|
|
|
| [1603] Mordon | 2012-10-31 15:00:07 |
 P az ABC háromszög belső pontja. A CP egyenes az AB oldalt a D, az AP egyenes a BC oldalt az E, a BP egyenes a CA oldalt az F pontban metszi. Tudjuk, hogy PA+PB+PC=43 és PD=PE=PF=3. Határozzuk meg a PA.PB.PC szorzat értékét.
Ennek a tavalyi Szőkefalvi feladatnak a megoldását valaki le tudná írni?
Előre is köszönöm!
|
|
|
| [1601] HoA | 2012-10-24 13:02:31 |
 Gondolom mivel a szereplő betük közül N a B mellett van a billentyűzeten, a kérdező B-t gondolt. Ekkor a metszéspont Jónás T pontja, a keresett hosszúságok AT = 4/5 AC = 4/5 * 28 cm = 22.4 cm, BT = 3/5 BC = 3/5 * 21 cm = 12.6 cm , mint [1597]-ben.
|
| Előzmény: [1596] jonas, 2012-10-23 22:01:37 |
|
|
| [1599] Blinki Bill | 2012-10-24 06:57:11 |
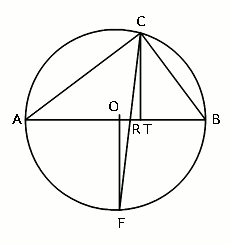
 Mivel F felezi az ívet, ezért CF a C-nél levő szög szögfelezője és az AB oldalt a szomszédos oldalak arányában osztja a szögfelező-tétel miatt. Az arány 3:4, így a 35cm-t kell ilyen arányban bontani, adódik 20cm és 15cm.
|
| Előzmény: [1595] Kásás János, 2012-10-23 20:10:04 |
|
|
| [1597] jonas | 2012-10-23 22:26:48 |
 A feladat első részéhez vedd észre, hogy a háromszög derékszögű.
Tegyük fel, hogy a BC oldal hossza 21 cm, az AC oldalé pedig 28 cm. Koordinátázzuk úgy a síkot, hogy a háromszög körülírt körének a középpontja legyen az origó, az A pont legyen a (-17.5 cm, 0), a B legyen (17.5 cm, 0), a C második koordinátája pedig legyen pozitív.
Jelölje T a C-hoz tartozó magasság talppontját. A talppont az AB átfogón úgy helyezkedik el, hogy az AT távolság egyenlő az AC befogó négyzete osztva az átfogóval, vagyis 22.4 cm. Ebből a T koordinátái (4.9 cm, 0). A CT magasság hossza egyenlő a befogók szorzata osztva az átfogóval, vagyis 16.8 cm, így a C koorindátája (4.9 cm, 16.8 cm).
Mármost az F pont a feladat szerint annak az ívnek a felezőpontja, aminek az átmérője az A és a B pont, ezért az F koordinátái (0, -17.5 cm). Ebből a CF szakasz metszete az AB koordinátatengellyel, amit hívjunk R-nek, (4.9cm.17.5cm/(17.5cm+16.8cm),0) = (-2.5cm,0). Ebből pedig az AR szakasz hossza 20 cm, az RB szakasz hossza pedig 15 cm.
|
| Előzmény: [1595] Kásás János, 2012-10-23 20:10:04 |
|
|
| [1595] Kásás János | 2012-10-23 20:10:04 |
 Segítséget szeretnék kérni tőletek, mert nem tudom megoldani a gyermekem házi feladatát:
Az ABC háromszög oldalainak hossza 21, 28 és 35 cm. A háromszög köré írt kört a háromszög csúcsai három ívre bontják. Ezek közül a leghosszabb ív felezőpontja F. Kössük össze F-et a háromszög szemközti csúcsával (legyen ez a csúcs C). Mekkora részre bontja a CF szakasz az AB szakaszt? Tükrözzük a C pontot az AN szakasz egyenesére (C’). Mekkora részre bontja a CC’ szakasz az AB oldalt?
A szögfüggvényeket még nem tanulták, azokat nem lehet használni.
Fáradozásotokat előre is megköszönve.
Tisztelettel: Kásás János
|
|
|
| [1593] m2mm | 2012-08-14 10:50:14 |
 Projektív megoldást találtam én is, elemi engem is érdekelne.
Ma böngészve régebbi KöMaL-példák között találtam a B.3680. feladatra, ami tulajdonképpen a 181. feladat nemtriviális része, így egy újabb megoldást rakhatunk a feladathoz, a hivatkozásban láthatunk egy újabb bizonyítást.
B.3680
|
| Előzmény: [1570] Vonka Vilmos Úr, 2012-05-27 20:25:16 |
|
|
|







 = 160 fok , így CAO
= 160 fok , így CAO 




 ,CFH
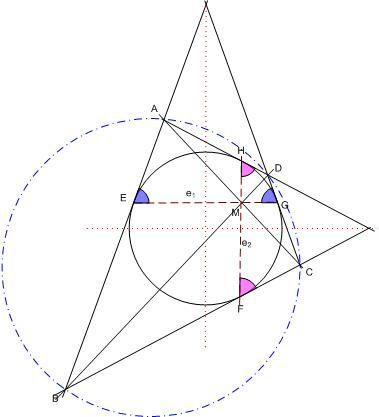
,CFH . Az érintőnégyszög szemközti, B-nél és D-nél lévő szögeinek összege az M-nél derékszögű MGDH és MEBF négyszögekből
. Az érintőnégyszög szemközti, B-nél és D-nél lévő szögeinek összege az M-nél derékszögű MGDH és MEBF négyszögekből  +
+ =(360–90-
=(360–90-