|
|
| [1638] HoA | 2013-01-21 18:19:23 |
 Az mindenesetre látszik, hogy ha az arány a szögektől független állandó, akkor csak 1/1 ( felezés ) lehet, mert ha  növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-) növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-)
|
| Előzmény: [1637] w, 2013-01-20 16:02:33 |
|
|
|
|
| [1634] Fálesz Mihály | 2013-01-16 22:21:16 |
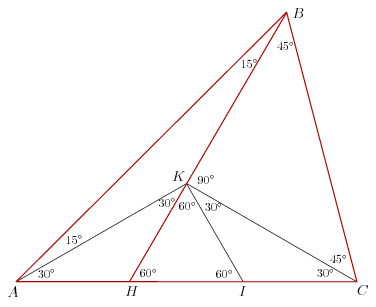
 Akkor egy megoldás csak egyenlő szárú háromszögekkel (és egy helyen tengelyes szimmetriával).
Legyen az AC másik harmadolópontja I, és rajzoljuk meg befelé a HIK szabályos háromszöget. A K pont a BH szakaszon van, mert AHB =120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek. =120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek.
Az AHK és CIK háromszögek egyenlő szárúak, innen kapjuk a bejelölt 30 fokos szögeket. Ezután BAK =15o, és az ABK háromszög is egyenlő szárú. Tehát AK=BK. A K rajta van az AC felező merőlegesén, így AK=CK. Végül a BCK háromszög is egyenlő szárú, mert BK=AK=CK, tehát BCK =15o, és az ABK háromszög is egyenlő szárú. Tehát AK=BK. A K rajta van az AC felező merőlegesén, így AK=CK. Végül a BCK háromszög is egyenlő szárú, mert BK=AK=CK, tehát BCK =CBK =CBK =45o. =45o.
|
 |
| Előzmény: [1632] w, 2013-01-16 19:44:03 |
|
| [1633] bily71 | 2013-01-16 22:20:37 |
 "- Valóban eltekinthetünk-e attól, hogy az S-en lévő háló oldalak nem egyenes szakaszok, hanem körívek?"
Eltekinthetünk, ha módosítunk kicsit az eljáráson, P csúcsait G1-re vetítjük, legyen A,B P két csúcsa, ekkor a köztük fut él illeszkedjen az A',B',O2 pontokon átmenő gömbi körre, ekkor az A'B' szakasz képe egy egyenesre illeszkedik, de ekkor további problémák léphetnek fel.
Egy másik mód, ha O pontból képezzük S síkra (mely sík illeszkedik P egy lapjára) P-t úgy, hogy minden él rövidebb, mint a képe, és a lapok képei nem fedik egymást, kivéve egy lapot, mely az egész képet fedi. Ilyen O pont létezik (számomra érdekes feladat volt meghatározni ezen pontok mértani helyét), de most már úgy látom, nem a leképezésen van a hangsúly, hanem F valamely tulajdonságán. Egyelőre elakadtam.
|
| Előzmény: [1625] HoA, 2013-01-07 10:28:40 |
|
| [1632] w | 2013-01-16 19:44:03 |
 :) Neked még hány ilyen "kalapácsod" van?
Van megfelelő eszköz, lehet nagyon elegáns (az alapvetőségi értelemben), de nagyon nehéz megoldást adni rá. Én max. az országos fordulón tűztem volna ki. Az előbbi hozzászólásomban felsorolt módszereket (tényleg, más nincs) alaposan át kell gondolni mindegyik lehetőséget. Tehát, találjunk egy alkalmas vonalat, amit behúzva csodák történhetnek!
|
| Előzmény: [1630] Fálesz Mihály, 2013-01-16 06:58:34 |
|
| [1631] HoA | 2013-01-16 09:11:02 |
 Rendben, azért még kérlek várj egy kicsit a "hetedikes" megoldás felrakásával. Hadd próbálkozzak egy [1615] jellegű pofonegyszerű változattal.
|
| Előzmény: [1629] w, 2013-01-15 17:49:16 |
|
| [1630] Fálesz Mihály | 2013-01-16 06:58:34 |
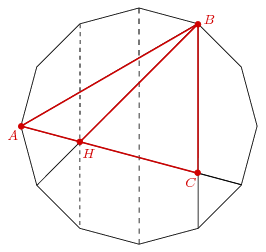
 Az én hetedikes gyerekem is volt ugyanezen a versenyen. Egyetértek, a feladat nagyon szerencsétlen, ilyen szinten nincs megfelelő eszköz, később meg már van trigonometria, amivel a feladatot le lehet dózerolni.
Btw nekem van egy elég nagy kalapácsom az ilyenekre, ezúttal nem a szabályos 18- hanem a 12-szög átlói között kell keresgélni.
|
 |
| Előzmény: [1629] w, 2013-01-15 17:49:16 |
|
| [1629] w | 2013-01-15 17:49:16 |
 Legközelebb ilyen feladatot a Találjunk jobb megoldást! témába rakok :). A megoldásod szép és elegáns, középiskolás ismeretek mellett talán a legszebb.
A következő használható 7-8-adikos szinten: belsőszög-összeg, váltószög, háromszög nevezetes vonalai, spec. négyszögek, területképletek, egybevágóság, Thales és Pitagorasz (egész számokkal). Stratégiáik: számítsunk szögeket, szakaszokat; nézzük meg a magasság-, súlypontot, beírt és körülírt kör kp.-ját; húzzunk be egy alkalmas vonalat.
Ezt a feladatot a Bátaszéki verseny megyei (II.) fordulóján tűzték ki. Statisztikát kéne csinálni arról, hogy hányan csinálták meg, eddig senkiről sem tudok, aki megoldotta volna rendesen.
|
| Előzmény: [1628] HoA, 2013-01-15 11:35:56 |
|
| [1628] HoA | 2013-01-15 11:35:56 |
 Nem tudom, a 7. osztályos versenyzőktől elvárható-e a gyökvonás , a Pitagorasz-tétel és a nevezetes szögekkel bíró háromszögekben az oldalak és magasságok méretviszonyainak ismerete ( szándékosan nem írok szögfüggvényeket ) . Ha igen, akkor az alábbi típusú megoldást tartom elvárhatónak:
Az AB oldalon vegyük fel J-t úgy, hogy ABH és HBJ hasonló háromszögek, majd BH-n K-t úgy, hogy HBJ és JBK hasonló háromszögek. A 45 - 60 - 75 fokos szögekkel rendelkező AJH és HKJ háromszögekben AH és HJ ill. HJ és JK arányából adódik, hogy AH = 3/2 * JK, így AB = 3 * AJ. JH és BC párhuzamosak, beta = 60 fok.
|
| Előzmény: [1627] w, 2013-01-14 21:15:51 |
|
| [1627] w | 2013-01-14 21:15:51 |
 Kíváncsi vagyok, mit kezdetek a következő (mostani) 7. osztályos versenyfeladattal (én szinusztétellel indultam neki :) , a szöveget másképp írtam le).
184. feladat: Az ABC háromszögben A-nál 45 fokos szög van, és a B csúcsból az AH szakasz 15 fokos szögben látszik. Mekkorák a háromszög szögei, ha H az AC oldalon van, és (ACH)=1/2?
|
|
|
| [1625] HoA | 2013-01-07 10:28:40 |
 "mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o"
Megmaradó aggályaim:
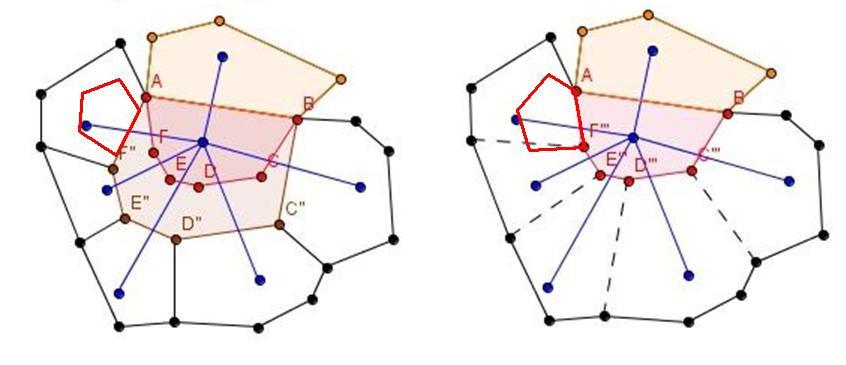
- Igaz, hogy az S-beli háló pl. F'' -ben összefutó szomszédos élei által bezárt szögek összege 360o , míg a konvex P F-ben ben összefutó szomszédos élei által bezárt szögek összege ennél kisebb. De mi garantálja, hogy az egyenlőtlenség a példánkban 3 szögpárra külön-külön is fennáll?
- Valóban eltekinthetünk-e attól, hogy az S-en lévő háló oldalak nem egyenes szakaszok, hanem körívek?
- És amire konkrét példám van: Nem változtatják-e meg az összehúzások a szögekre vonatkozó szükséges feltételeket?
Tegyük fel, hogy [1622] bal alsó ábráján az AF'' szakasz bal oldalán elhelyezkedő háló ötszög F'' -nél lévő szöge kb. 90o , mint az ábrán. Ebbe szépen elhelyezhető P AF-hez csatlakozó ötszögű lapja, melynek F -nél lévő szöge mondjuk 85o . Egy összehúzás után [1622] jobb alsó ábráját kapjuk, ahol az AF''' szakasz bal oldalán elhelyezkedő háló ötszög F''' -nél lévő szöge kb. 80o , mint az ábrán. Ide lefordítva P AF-hez csatlakozó ötszögű lapját, az ki fog lógni a rendelkezésre álló háló ötszögből.
|
| Előzmény: [1624] bily71, 2012-12-27 23:35:55 |
|
| [1624] bily71 | 2012-12-27 23:35:55 |
 Az élek második képe körív hiszen, ha O1-ből végigpásztázunk egy élet, akkor egy síkrészt kapunk, mely metszi a G1 gömböt, a metszet ekkor természetesen körív, így P egy élének első képe G1 egy főkörén van. Ha invertáljuk ezt a kört, akkor megint kört kapunk, vagyis egy él második képe az S síkon fekvő körön van. Mindezeket figyelembe vettem, de egyszerű ábrát akartam készíteni, mert valójában ennek nincs jelentősége. Az E''G' ívből mindegy mi lesz, mert P átforgatásakor az újonnan S-re érkező csúcsok nem lehetnek benne a vetület megfelelő összehúzásokkal már módosított tartományában a következő okok miatt.
Az összehúzást L-1-gyel kezdjük, majd átbillegtetve P-t L1 élein összehúzzuk a megnyúlt szomszédjait is. Utoljára az (ii) szerint kiválasztott L2-t húzzuk össze. Az L1 lap és szomszédai egy síkidomot határoznak meg S-n, melynek körvonala és L1 szomszédainak közös élei mentén, kivéve L2 azon éleit, miket F metsz, az S át van vágva. Miután L1-et a szomszédaival összehúztuk, a kapott síkidom körvonala eltávolodik a régi körvonaltól, mégpedig az összehúzott lapok irányába, így az összehúzott lapok nem metszetnek bele a nem összehúzott lapokba. L-1 szomszédai az összehúzás után nem metszethetnek bele L1-be, sem egymásba, hiszen L1-t szomszédaival együtt kiterítve a síkba a szomszédok közös élei nemhogy fedik egymást, hanem eltávolodnak egymástól. Ez azért van, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
Mikor L2-t és szomszédait összehúzzuk, az L1 és L2 szomszédai által alkotott síkidom új körvonala eltávolodik a régitől, mint az előbb, tehát ez a síkidom sem metsz bele a nem összehúzott lapokba, vagyis nem keletkezik átfedés. L2 még nem összehúzott szomszédait összehúzva (itt is billegtetünk L3 a végére hagyva) az L2 újonnan összehúzott szomszédai nem metszetnek bele L2-be, sem egymásba ugyanazon okokból kifolyólag, mint amit leírtunk már L1 és szomszédai esetében. L2 újonnan összehúzott szomszédai nem metszethetnek bele az előbb összehúzott lapokba sem, hiszen akkor belemetszenének L2 már előzőleg összehúzott szomszédaiba is, ami nem lehet megint csak az előbbiekben már említett okokból. Átfedés tehát itt sem keletkezett.
Az előbbi gondolatmenetet alkalmazhatjuk L3-ra, L4-re és így tovább...
A lényeg még egyszer: Lk újonnan összehúzott szomszédai nem metszethetnek bele az előzőekben összehúzott lapok által alkotott síkidomba, mert akkor belemetszenének Lk már előzőleg összehúzott szomszédaiba is, ami nem lehet, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
|
| Előzmény: [1623] HoA, 2012-12-27 15:04:35 |
|
| [1623] HoA | 2012-12-27 15:04:35 |
 További kellemes évvégét és évelejét mindenkinek!
Nem tudom, figyelembe vetted-e, és mert nem befolyásolja eredményeidet, egyszerűsítetted [1622] ábráját, minden esetre az S síkon a kétvesszős pontokat összekötő vonalak nem egyenes szakaszok.
[1617] metszet ábrájában persze a metsző sík O1 -en és O2 -n is áthalad, így az A'B' gömbi főkör ívet O2 -ből S-re vetítve egyenest kapunk. Ez azonban általában nem így van. A'B' az O1AB sík és G1 metszésvonala, G1 főköre. Ha ez nem megy át O2 -n, akkor a vetület S-en zárt görbe ( emlékezetem szerint kör ) lesz, melynek egy ívdarabja a háló A''B'' közötti vonala.
[1622] ábrája ígéretes, de még mindíg nem látok olyan állítást és annak bizonyítását, ami garantálná, hogy a végeredményül adódó kiterítésben nem lehet átfedés. Például: "P átforgatásakor az újonnan S-re érkező P csúcsok benne vannak a vetület megfelelő, esetleg összehúzásokkal már módosított tartományában". E'' jelöletlen szomszédját G'' -vel jelölve az összehúzás során mi lesz az E''G'' ívből? Egyenes szakasz? Vagy ha körív, akkor mekkora sugarú?
|
| Előzmény: [1622] bily71, 2012-12-26 23:24:30 |
|
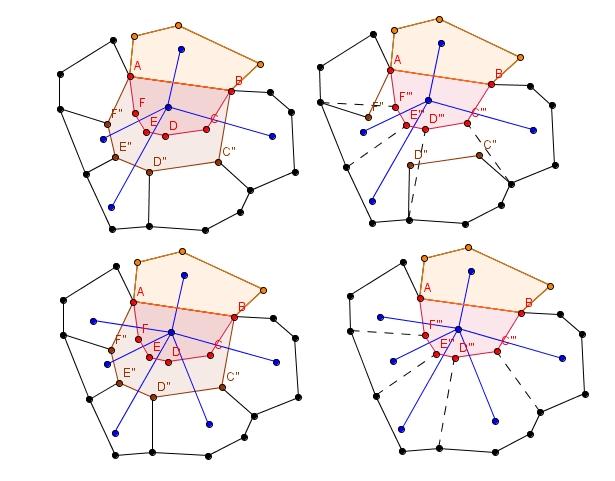
| [1622] bily71 | 2012-12-26 23:24:30 |
 "Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi."
Átnéztem és átgondoltam. Az F fának a következő feltételeknek kell eleget tennie (F-et az egyszerűség kedvéért rajzolhatjuk közvetlenül P-re is).
(i) Az Li lapra (melyet az O1O2 egyenes döf) illeszkedő csúcs levél.
(ii) Létezik F1, F2, ..., Fm fa gráf sorozat úgy, hogy F1 egyetlen, az S síkkal párhuzamos L1 lapra illeszkedő csúcsból áll (ez legyen F gyökere),  , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak. , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak.
Az ábrán (mely csak egy elképzelt esetet ábrázol) azt láthatjuk, mikor P-t átforgatjuk az AB élen, és az ABC''D''E''F'' lapot ráhúzzuk ABCDEF lapra. Az ábra felső részén látható, hogy ha nem (ii) szerint építjük fel F-et, akkor az összehúzás közben bár a összehúzott lap nem fed át egy lapot sem, de a megnyúlt szomszédainál felléphet átfedés, és nem tudhatjuk, hogy az megszűnik-e.
Az alsó részen módosítottuk F-et (ii) szerint, így a megnyúlt lapoknál sem lép fel átfedés. Most már kimondhatjuk, hogy az előbbi feltételeknek eleget tevő F szerint kiterítve P-t nem lép fel átfedés, és pont ezt akartuk megmutatni.
Amúgy kellemes ünnepeket! :)
|
 |
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1621] bily71 | 2012-12-23 20:44:42 |
 Igen, (ezt a "bizonyítást" a közzététel előtti álmatlan éjszakámon ötlöttem ki, csak úgy eszembe jutott) azon már a legelején gondolkoztam, hogy a "felső", vagyis az Li' lapot, amelyiket az O1O2 szakasz átdöfi, nem kellene hozzávenni a fához (ami így nem is, vagy hiányos feszítőfa), hanem utána biggyesztenénk oda az F* hiányos feszítőfa valamelyik levele után (de melyik után?), ugyanis ennek képe Li'' nem korlátos, nem világos, hogy mi történik vele az összehúzás közben, de később annyira nyilvánvalónak tűnt minden, hogy nem foglalkoztam vele.
Azonban úgy tűnik, hogy ha az Li'' nélküli sokszögre alkalmazzuk az összehúzást, akkor nem kapunk átfedést, még átgondolom, de annyira egyértelműnek tűnik.
|
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1620] HoA | 2012-12-23 16:24:41 |
 Én nem tudok, mivel eddig sohasem foglalkoztam ezzel a problémával, csak felszólításodra néztem bele. A "Dürer sejtés" Wikipedia oldalán azonban látható ez a hivatkozás:
http://www.ams.org/samplings/feature-column/fcarc-nets
Ebben megtalálhatod az alja felé a két következő idézetet:
"Her work related to finding a way of generating random 3-dimensional convex polyhedra and then choosing a random unfolding (not such simple issues) and seeing if the random unfolding overlapped. Her results showed that as the number of vertices of the solid increased, for a fixed specific solid the number of unfoldings where an overlap did occur increased" . ( Amiből itt csak az az érdekes, hogy növekvő csúcsszámmal növekszik azoknak a kiterítéseknek a száma, ahol átfedés van. ) És
"...no matter what reasonable type of tree Schlickenrieder picked, he was able to find examples of 3-dimensional convex solids where this tree did not lead to a net unfolding without overlaps." ( vagyis adott típusú fákat vizsgálva Sch.-nak sikerült olyan fát találni, mely nem vezetett átfedés nélküli kiterítésre )
A lényeg: A sejtés konvex poliéderekre sem azt mondja, hogy minden kiterítés átfedésmentes, hanem csak azt, hogy létezik átfedésmentes kiterítés. A Wikipédia cikk szerint "Dürer sejtette, hogy minden poliédert fel lehet vágni az élei mentén úgy, hogy lapjai (átfedés nélkül) kiteríthetőek legyenek a síkban, egy összefüggő sokszöget képezve." - és nem azt, hogy minden kiterítés ilyen.
Mivel te F megválasztására semmilyen különleges feltételt nem adtál meg, módszered az említett átfedéses kiterítéseket is létrehozná, tehát valahol a bizonyításban lehet a hiba. Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi.
|
| Előzmény: [1619] bily71, 2012-12-23 15:31:46 |
|
| [1619] bily71 | 2012-12-23 15:31:46 |
 Persze, hogy nem látod, mert a két sokszög ugyanaz. A különbség az út, hogy hogyan jutunk a sokszögig. Közvetlenül is felrajzolhatjuk H-t és F-et, majd szétvághatjuk, de attól még nem tudjuk, hogy lesz-e átfedés. Mutattam egy utat, ahol úgy kapjuk meg a sokszöget, hogy egyik lépésben sem keletkezik átfedés. Tulajdonképp azt próbálom demonstrálni, hogy H bármely F feszítőfája jó.
Most azért elbizonytalanítottál. Létezik olyan F, hogy a szétvágás és kiterítés során átfedést kapunk? Ha megkérlek, mutatnál erre példát?
|
| Előzmény: [1618] HoA, 2012-12-23 00:40:02 |
|
| [1618] HoA | 2012-12-23 00:40:02 |
 Nem látom, mi a különbség a módszereddel kapott síkbeli sokszög és aközött, hogy H-t - és így F-et - közvetlenül P-re rajzoljuk és P-t felvágjuk az F élei által nem metszett poliéder élek mentén. Vagyis kérlek mutass egy példát arra, ahol a két eredményül kapott sokszög különböző. Mert ha a két sokszög ugyanaz, akkor...
|
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
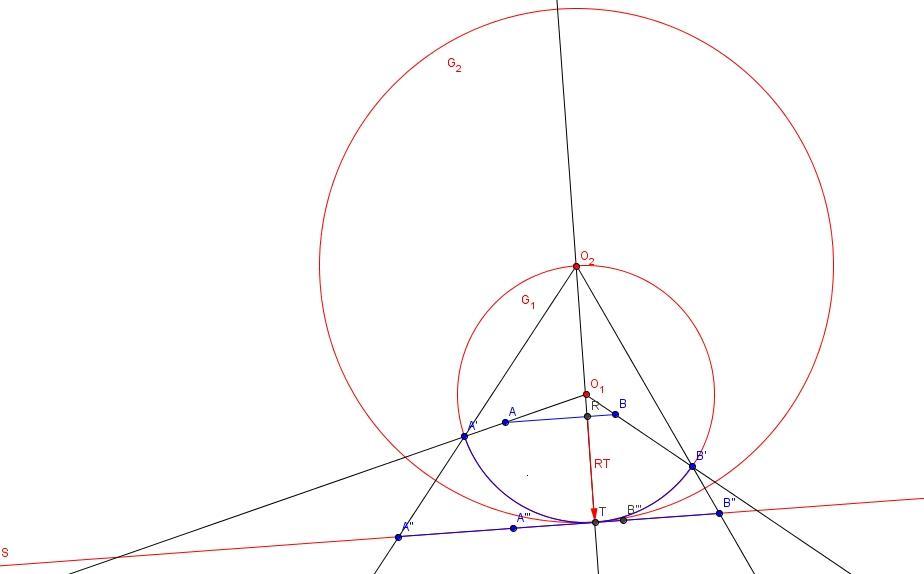
| [1617] bily71 | 2012-12-22 23:07:33 |
 Azért több érdeklődést vártam. Ha jól tudom, a Dürer-sejtés még nyitott, Bezdek Dániel csak speciális estben bizonyította. Ha az előbbi megoldás jó, akkor én a poliéderek bővebb halmazán bizonyítottam.
Készítettem egy ábrát, melyen két dimenziós metszetben P egy lapjára illeszkedő szakaszon mutatom be, hogy mit is csináltunk P-vel. Az AB szakaszt O1-ből G1 körre vetítjük, majd a kapott A'B' körívet O2-ből S-re invertáljuk, így kapjuk az A''B'' szakaszt. Ezek után eltoljuk AB-t 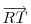 vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók. vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók.
Az A''B'' szakasz mindig nagyobb, mint az AB. Ugyanígy, mikor P-t görgetjük (elforgatjuk az éle, mint tengely körül), a görgetett lap mindig része a második képének, tehát összehúzást kell alkalmaznunk, hogy a harmadik kép egybevágó legyen az eredetivel. Az összehúzás során az átvágott élek mentén a szomszédos lapok eltávolodnak, vagyis rés keletkezik a síkon, így nem keletkezhet átfedés, a nem átvágott élek mentén pedig a szomszédos lap megnyúlik az összehúzás irányában, de átfedés itt sem keletkezik. Szemléletesen az történik, hogy felszabdaljuk az S síkot, majd az összehúzás transzformációval a síkrészeket ráhúzzuk P lapjaira, vagyis az egész S síkot ráképezzük P-re. (Ez nem egy szokványos transzformáció, hiszen két összehúzás között P-t ide-oda mozgatjuk.) Ez lenne a levezetés lényege. Kíváncsian várom a véleményeket.
|
 |
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
| [1616] bily71 | 2012-12-21 22:42:34 |
 183. feladat. Adott P 3 dimenziós konvex poliéder. Terítsük ki P lapjait a síkba úgy, hogy átfedés nélkül egy összefüggő sokszöget alkossanak, azaz adjuk meg P egy hálóját!
Megoldás. Helyezzük P-t egy 3 dimenziós G1 gömbbe úgy, hogy az O1 gömb középpont P egy belső pontja legyen, továbbá P minden pontja G1 belső pontja legyen! Vetítsük P-t O1-ból G1 felszínére úgy, hogy ha Q pont P egy élének egy pontja, akkor Q' pont az O1Q egyenes és G1 felszínének metszete! Ekkor egy gömbre rajzolt P' gráfot kapunk.
Válasszuk ki P' minden lapjának egy belső pontját, (azaz a P' gömbre rajzolt gráf körei által határolt gömbfelszín tartományok egy belső pontját), majd kössük össze ezeket, ha két szomszédos lap, (azaz közös éllel rendelkező lapok) belső pontjai! Ekkor egy H gráfot kapunk. Legyen F H egy feszítő fája!
Sztereografikus projekciót alkalmazva képezzük P'-t és F-et az S síkra! S párhuzamos P egy lapjával, T pontban érinti érinti G1-et, ugyanitt érinti G2-t, az inverzió gömbjét, melynek O2 középpontja T átellenes pontja G1-en, továbbá O2 nem csúcsa P'-nek és F-nek, és nem illeszkedik P' és F egyik élére sem. Ekkor egy síkba rajzolt P'' gráfot és egy F' fát kapunk.
Legyen az R pont P, az S síkkal párhuzamos, L1 lapja és az O1T egyenes metszete! Toljuk el P-t az 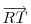 vektorral! Ekkor L1 eltolt képe illeszkedik S-re. vektorral! Ekkor L1 eltolt képe illeszkedik S-re.
Gondoljunk S-re úgy, mint vastagság nélküli rugalmas, vágható anyagból álló felületre! Vágjuk át S-t azon élek mentén, melyeket nem metsz F' egyik éle sem!
Legyen az L1 lap egy csúcsa V1, húzzuk bele V1''-t V1-be! Ismételjük ezt L1'' minden csúcsával! Az "összehúzás" transzformáció után L1'' képe egybevágó lesz L1-gyel, hisz fedik egymást.
Gördítsük át az eltolt P-t az egyik élén az S síkon az F' fa egy éle mentén, vagyis P egy olyan élén, mely metszi F' egy élét. Ekkor az L2 lap illeszkedik S-re, úgy, hogy az L1,L2 lapok közös éle fedi az összehúzott L1'' és a félig összehúzott L2'' lapok közös élét, továbbá L2 része L2''-nek. Legyen V2 az L2 lap egy csúcsa! Húzzuk bele V2''-t V2-be! Ismételjük ezt L2'' minden csúcsával! Az összehúzás után L2'' képe fedi L-2-t, így azok egybevágók. Az összehúzott L1'',L2'' lapok nem fedik át egymást. Az összehúzott L2'' nem fedi át egyik vele szomszédos másik lapot sem, hiszen vagy át van vágva az S sík a közös él mentén, így inkább távolodott szomszédjától, mivel az helyben maradt, vagy a közös élt metszi F'-et, ekkor nem keletkezik átfedés.
Gördítsük végig P-t F' minden útján az utak valamilyen sorrendjében! Egy út végére érve gördítsük visszafelé az úton P-t, míg az L1 lap nem illeszkedik újra S-re! Minden gördítés során alkalmazzuk az összehúzás transzformációt!
F' minden útját végigjárva egy összefüggő sokszöget kapunk, mely sokszög P lapjaival egybevágó sokszögekből áll, így a sokszög területe és P felszíne egyenlő, vagyis eleve kizárt, hogy a gördítések során átfedés keletkezett. Az S sík átvágása miatt az összehúzás során megkettőződött éleket újból fedésbe hozva P-vel egybevágó poliédert kapunk (a sokszögből visszahajtogathatjuk P-t), vagyis a feladatot sikerült megoldanunk.
P tetszőleges volt, ezért a feladatot megoldva egyúttal konstruktív bizonyítást adtunk Dürer sejtésére abban az esetben, ha a poliéder konvex.
Boldog Világvégét! :)
|
|



 /2 ), OL és JN párhuzamosak, így PJ és LK ( LM ) is párhuzamosak , AJP és AML hasonló háromszögek, AP = AD + DP = 2 AT + 2 TL = 2 AL , AJ = 2 AM.
/2 ), OL és JN párhuzamosak, így PJ és LK ( LM ) is párhuzamosak , AJP és AML hasonló háromszögek, AP = AD + DP = 2 AT + 2 TL = 2 AL , AJ = 2 AM.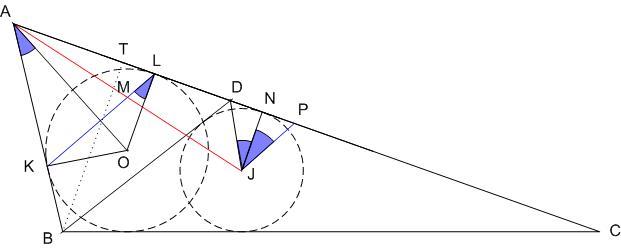

 <
<

 =120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek.
=120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek.