| [1692] Sinobi | 2013-04-26 20:08:45 |
 Borzasztó sok olyan görbe létezik, amin rajta van egy (na jó, kettő) meghatározott pont. :) Egyre kevésbé hiszem azt, hogy a feladatod megszerkeszthető, lehet, hogy létezik szép megoldás mondjuk vonalzóeltolással, fapálcikákkal, kötél és rajzszög alapú ellipsziszővel etc. de nem látok ilyet.
|
|
| [1691] ibiro | 2013-04-26 12:31:40 |
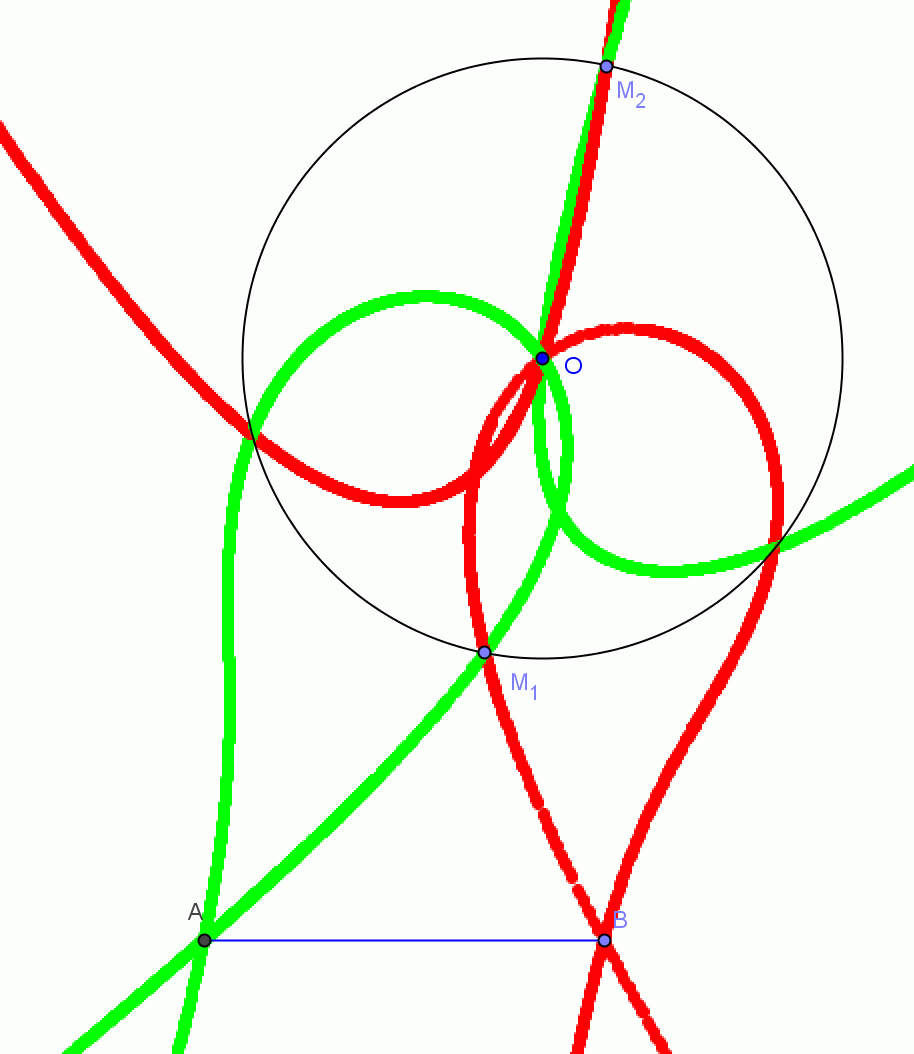
 "Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik" ... de honnan veszed hogy ellipszis pontok - ez csak a te feltételezésed ! Bízonyisd be és akkor elhiszem.
Sinobi [1680] szerint egy "csúnya csigabigán", szerinted egy "elfajult ellipszisen" , szerintem pedig egy hurkon és egy parabolán vannak. Igaza van-e valakinek ??? Addig senkinek amig nem jön bízonyitással.
|
 |
| Előzmény: [1690] HoA, 2013-04-25 11:21:01 |
|
| [1690] HoA | 2013-04-25 11:21:01 |
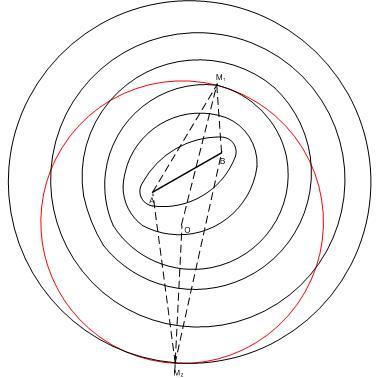
 A körön belüli általános helyzetű A és B pontokhoz mint fókuszokhoz tartozó ellipszisek az AB szakasztól, mint elfajult ellipszistől az "AB felezőpontja körüli nagyon nagy sugarú majdnem-kör" -ig ( elnézést a pongyola fogalmazásért ) folytonosan nőnek a nagytengely folyamatos növelésével. A legkisebbeknek nincs közös pontjuk a körrel. Lesz egy olyan, melynek egy közös pontja van a körrel, ez M1, ezután lesznek olyanok, melyeknek több közös pontjuk van a körrel. Eljutunk egy olyan nagy ellipszisig, melynek ismét csak egy közös pontja lesz a körrel M2 . Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik. Talán csak annyiban kell szigorítani a fenti gondolatmenetet, hogy belássuk: ha egy körnek és egy ellipszisnek csak egy közös pontja van, akkor az érintési pont és így az itt húzott érintő egyenesek azonosak. Ebből már következik a feladat feltételének teljesülése.
|
 |
| Előzmény: [1689] ibiro, 2013-04-25 08:09:39 |
|
| [1689] ibiro | 2013-04-25 08:09:39 |
 Ehhez kellene bizonyitani hogy MA+MB állandó, de mi van akkor ha az ellipszis a kör belsejében lesz és nem érinti a kört ? A feladat nem mond semmit a kör és a szakasz helyzetéről.
|
| Előzmény: [1688] HoA, 2013-04-24 13:18:49 |
|
|
|
|
|
| [1684] Kemény Legény | 2013-04-20 19:06:18 |
 A koszinusztételes megoldást kicsi jobban "be lehet csomagolni" vektorok (és azok skaláris szorzatának) használatával. Ha az OA,OB,OC,OD,OP vektorokat rendre a,b,c,d,p jelöli, akkor
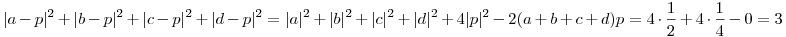 , mert a+b+c+d=0. , mert a+b+c+d=0.
|
| Előzmény: [1683] Layven, 2013-04-20 18:47:24 |
|
| [1683] Layven | 2013-04-20 18:47:24 |
 Igen, ez lehetőségként végig megvolt bennem, de az nem lett volna szép megoldás. Végül sikerült megoldani koordináták nélkül.(ABCD négyzet csúcsai, O a középpontja,P a kiválasztott pont a beírt körön.)
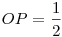 , , 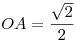
Koszinusztétel az AOP háromszögben:
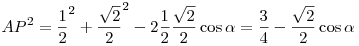
Felírva mindegyik oldalt hasonlóképpen és összegezve:
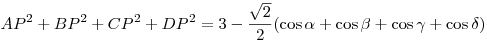
Most megmutatjuk, hogy a koszinuszok összege 0. A, O és C pontok egy egyenesben vannak, tehát AOP +POC +POC =180o, azaz =180o, azaz  + + =180o, hasonló módon pedig =180o, hasonló módon pedig  + + =180o =180o
Ismert, hogy 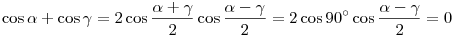
Hasonló módon kijön,hogy cos  +cos +cos  =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3 =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3
|
| Előzmény: [1682] Sinobi, 2013-04-20 12:32:17 |
|
| [1682] Sinobi | 2013-04-20 12:32:17 |
 Próbáld koordinátákkal. Vegyél fel egy P(Xp,Yp) pontot, és számold ki egy (mondjuk origó középponttú) egységnégyzet csúcsaitól a távolságnégyzetek összegét.
|
| Előzmény: [1681] Layven, 2013-04-20 11:32:22 |
|
| [1681] Layven | 2013-04-20 11:32:22 |
 A következő problémán akadtam fent: Bizonyítsuk be, hogy ha ABCD egységnégyzet beírt körén lévő pont P, akkor AP2+BP2+CP2+DP2=3
|
|
| [1680] Sinobi | 2013-04-13 19:10:10 |
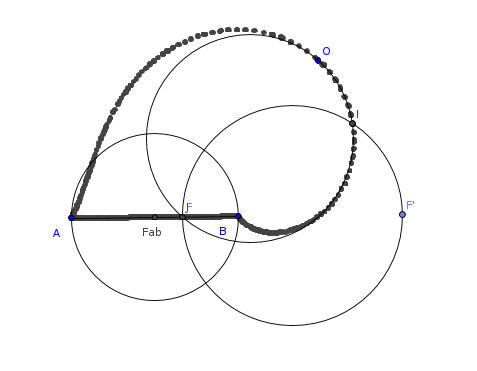
 Az olyan I pontok halmaza, ahol I rajta van AB F-hez tartozó szögfelezőkörén, és az FO tháleszkörén, (azaz AIB szögfelező talppontja F és FIO merőleges) egy csúnya csigabigán vannak. Kérdés: igaz-e, hogy ha meg tudjuk szerkeszteni valahogy a csúnya csigabiga és minden O középponttú kör metszéspontjait, akkor a csúnya csigabiga és egy tetszőleges kör ill. és egy tetszőleges egyenes metszéspontjait is.
|
 |
| Előzmény: [1679] ibiro, 2013-04-05 13:09:20 |
|
| [1679] ibiro | 2013-04-05 13:09:20 |
 Adott az AB szakasz és az O középpontú R sugarú kör. Határozzuk meg azt az M pontot (pontokat) a körön melyre az OM egyenes az AMB szög szögfelezője.
|
|
| [1678] HoA | 2013-04-04 14:16:15 |
 RE: "Q pontot pedig abban az esetben kapjuk, ha X a P pont PQ felezőmerőlegesére vett tükörképe"
Valójában Q pontot abban az esetben kapjuk, ha T a Q-ból e-re pocsátott merőleges talppontja és X a P pont T-re vett tükörképe.
|
| Előzmény: [1670] Vonka Vilmos Úr, 2013-04-03 13:10:24 |
|
|
| [1676] w | 2013-04-03 21:16:14 |
 Nem értem a bajt: egy triviális példát mondtál az állítás igazságára. Megint: ha egy téglalap kirakható 1xm-es és nx1-es lapok együttesével, akkor alkalmas lapot kiválasztva, csak azzal is kirakható.
|
| Előzmény: [1675] Róbert Gida, 2013-04-03 20:34:17 |
|
| [1675] Róbert Gida | 2013-04-03 20:34:17 |
 Legyen m=n=2, továbbá a nagy téglalap amit parkettázunk pedig 2x2-es. Ekkor ez kiparkettázható 1 x m -es és n x 1 -es téglalapokkal. De kiparkettázható csak 1 x m-es vagy csak n x 1-esekkel is.
|
| Előzmény: [1664] w, 2013-04-01 23:11:31 |
|
| [1674] Vonka Vilmos Úr | 2013-04-03 19:14:09 |
 A mértani hely meghatározására elemi megoldást egyelőre nem találtam, a hiperbolák fókuszait azonban meg lehet keresni.
Érdemes észrevenni, hogy mindkét hiperbola középpontja a PQ szakasz F felezőpontja. Valóban: ha például a T pontot F-re tükrözve kapott pontot T' jelöli és X'=e QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik. QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik.
Szóval a t hiperbolának az aszimptotáinak ismerjük az irányát (e-vel párhuzamos illetve merőleges egyenesekről van szó), és tudjuk, hogy F-re illeszkednek. Az aszimptoták ismeretében pedig szerkeszthetőek a tengelyek (szögfelezőként), és a hiperbola egy további pontjának (például P) ismeretében a fókuszok is. (Meg is szerkesztettem a fókuszokat; de azt nem látom egyelőre, hogy mi az elemi geometriai jelentésük, ami alapján elemibb megoldást lehetne adni a feladatra.)
Akkor néhány szó a Steiner-tételről. Két sugársor közötti projektivitáson a két sugársor közötti kettősviszonytartó, bijektív megfeleltetést értünk.
Tétel. Tekintsünk két sugársor között egy projektivitást. Az első sugársor minden egyenesének képezzük a metszéspontját a hozzá rendelt egyenessel. Az így kapott metszéspontok egy kúpszeletre (vagy speciális esetben egy egyenesre) illeszkednek. Amennyiben a metszési alakzat kúpszelet, az tartalmazza a sugársorok tartópontjait.
Vázlatosan egy viszonylag elemi bizonyításról: Legyenek a sugársorok tartópontjai P és Q, valamint a metszési alakzat három pontja A, B és C. Ez azt jelenti, hogy a projektivitásban a PA, PB, PC egyenesek képei rendre a QA, QB, QC egyenesek (a kettősviszonytartás miatt ez a három egyenespár egyértelműen meghatározza a projektivitást). Tegyük fel, hogy az A, B, C pontok nem kollineárisak; ekkor van egy és csak egy olyan k kúpszelet, amely az A, B, C, P, Q pontokra illeszkedik. (Öt pont egyértelműen meghatároz egy kúpszeletet, ez pl. a Pascal-tétel miatt ismert.) Azt kell ellenőriznünk, hogy egy D pont akkor és csak akkor illeszkedik k-ra, ha a tekintett projektivitásban PD képe QD. Másként fogalmazva: D akkor és csak akkor van k-n, ha a (PA,PB,PC,PD) és (QA,QB,QC,QD) kettősviszonyok egyenlőek. Ez azonban a kerületi szögek tételének alkalmazásával közvetlenül következik, ha egy kollineációt (tehát kettősviszonytartó leképezést) alkalmazva a k kúpszeletet körbe transzformáljuk. (A hozzáértők nyilván láthatják, hogy a bizonyítás nehézségeit hány ponton "kentem el" bizonyos "jól ismert" tényekre hivatkozva; a téma részletes kifejtése azonban jóval túlmutat a fórum keretein.)
|
| Előzmény: [1672] w, 2013-04-03 16:59:24 |
|
| [1673] w | 2013-04-03 17:33:18 |
 A Te feladatodra ez a megoldás nem igazán használja ki, hogy két dimenzióban van, nagyon szép ötlet.
Az általam kitűzött feladat térbeli változata "lemészárolható", csak a megoldással még várnék.
|
| Előzmény: [1668] Fálesz Mihály, 2013-04-03 10:01:27 |
|
| [1672] w | 2013-04-03 16:59:24 |
 A megjegyzésben szereplők érdekelnek leginkább. Mi Steiner tétele? Be tudnád-e bizonyítani? Létezik-e a feladatomnak elemi megoldása: hol és hogyan találhatjuk meg a két hiperbola fókuszait/vezéregyeneseit?
w
|
| Előzmény: [1670] Vonka Vilmos Úr, 2013-04-03 13:10:24 |
|
| [1671] Fálesz Mihály | 2013-04-03 14:48:35 |
 Nem értem.
"... a téglatest egy oldalára a kis téglatesteknek csak olyan lapja fekszik, aminek van egész oldala"
Miért ne lehetne valamelyik kis téglának az adott lapra merőleges éle az egész hosszúságú?
|
| Előzmény: [1669] jonas, 2013-04-03 10:24:34 |
|
| [1670] Vonka Vilmos Úr | 2013-04-03 13:10:24 |
 Gondolom, hogy úgy értetted a feladatot, hogy a Q ponton keresztül felvett tetszőleges másik egyenest rögzítjük, és azon a rögzített f egyenesen változik az Y pont.
Az egyszerűen látható, hogy mindkét mértani hely tartalmazza a P és Q pontokat. A t mértani hely esetén P=X választással adódik a P pont; a Q pontot pedig abban az esetben kapjuk, ha X a P pont PQ felezőmerőlegesére vett tükörképe.
További közös pontok csak abban az esetben találhatóak, ha e és f párhuzamosak. Valóban: tegyük fel, hogy M közös pont, és tekintsük az e illetve f egyenes M-hez tartozó X illetve Y pontját. (Tehát azokat az X illetve Y pontokat, amelyekből kiindulva a konstrukcióddal T=U=M adódik.) Ekkor PMX és QMY egyaránt egyenlő szárú háromszögek, valamint a (PMY) és (QMX) ponthármasok kollineárisak. Így a két egyenlő szárú háromszöget tekintve a szárszögek egybevágóak, ezért az alapon nyugvó szögek is. Ebből az e és f egyenesek párhuzamossága következik.
Az egyszerűen ellenőrizhető, hogy e és f párhuzamossága esetén a két mértani hely egybeesik: ebben az esetben az e egyenes valamely X pontjából kiindulva kapott T ponthoz TP f-et Y-nak választva U=T adódik. f-et Y-nak választva U=T adódik.
Összefoglalva: t és u közös pontjai pontosan P és Q, ha e és f nem párhuzamosak; ha pedig e és f párhuzamos, akkor az összes pont közös.
Megjegyzem, hogy t és u mindegyike derékszögű hiperbola. Az, hogy a mértani helyek kúpszeletek, projektív geometriai úton (Steiner tétele alapján) egyszerűen látszik. Például t ugyanis az e pontjait Q-ból vetítő sugársor és a PX szakaszok felezőmerőlegesei által alkotott sugársor metszési alakzata. Ez a két sugársor projektív kapcsolatban van, így a metszési alakzatuk kúpszelet. Ez a kúpszelet tartalmazza a sugársorok tartópontjait: tehát a Q pontot, illetve az e-re merőleges irányt jelentő ideális pontot. Tartalmazza továbbá e ideális pontját is, ugyanis abban az esetben, ha X az e egyenes ideális pontja, akkor T ugyanez az ideális pont. Így a mértani hely olyan kúpszelet, amelynek két ideális pontja merőleges irányokat jelent, azaz valóban derékszögű hiperbola.
|
| Előzmény: [1667] w, 2013-04-02 14:15:13 |
|
| [1669] jonas | 2013-04-03 10:24:34 |
 Ha az [1665]-ben lévő feladatot elhisszük, akkor ez az első térbeli változat már következik, hiszen a téglatest egy oldalára a kis téglatesteknek csak olyan lapja fekszik, aminek van egész oldala, ezért a téglatestnek kell lennie legalább két egész élének.
|
| Előzmény: [1668] Fálesz Mihály, 2013-04-03 10:01:27 |
|
| [1668] Fálesz Mihály | 2013-04-03 10:01:27 |
 Ne rohanjunk ennyire.
Oldjuk meg mindkét változatot, és keressünk olyan módszereket, amik magasabb dimenzóban is működnek. Pl. egy háromdimenziós téglát bontunk n×1×1, 1×m×1 és 1×1×k méretű darabokra, illetve olyan kis téglákra, amiknek van egész hosszúságű éle.
|
| Előzmény: [1667] w, 2013-04-02 14:15:13 |
|










 +POC
+POC +
+ +
+ =180o
=180o 


 QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik.
QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik. 
