Fórum: GEOMETRIA

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78]

Szeretnél hozzászólni? Jelentkezz be.

[373] Hajba Károly	2006-02-23 22:47:59
Huú! De nagy lett itt a forgalom. :o) És ez a pont könnyen szerkeszthető. Az oldalfelezőből a szemközti csúcs szögfelezőjével párhuzamost húzunk.

Előzmény: [369] jonas, 2006-02-23 22:34:34

[372] jonas	2006-02-23 22:45:46
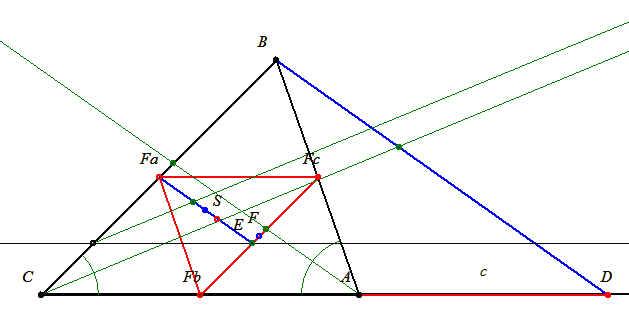
Akkor a keresett pontot úgy is megkaphatjuk, hogy az eredeti háromszög beírt körének középpontját -1/2-szeresére nagyítjuk az eredeti háromszög súlypontjából, vagy úgy is, hogy az eredeti háromszög csúcsait b+c,c+a,a+b arányban súlyozzuk. (Hol is van az a háromszög-nevezetes-pont-katalógus?)
Előzmény: [369] jonas, 2006-02-23 22:34:34

[371] lorantfy	2006-02-23 22:41:25
Az F_cEF_a háromszög hasonló CDB háromszöghöz, így az F_c-ból induló szögfelező a szemközti oldalt éppen (b+c)/a arányban osztja. Tehát S pont az F_aF_bF_c háromszög szögfelezőinek metszéspontja, vagyis a beírt körének középpontja.

Előzmény: [369] jonas, 2006-02-23 22:34:34

[370] lorantfy	2006-02-23 22:35:20
Igen! A szerkesztés ábrájából is látszik és könnyen bizonyitható.
Előzmény: [368] jonas, 2006-02-23 22:29:56

[369] jonas	2006-02-23 22:34:34
Azzal hogy az egyes oldalakat drótból készítenénk el, egyenértékű, ha az oldalak felezőpontjába rakunk az oldalhosszal arányos súlyokat, és ezeknek a súlypontját keressük. Na de a középvonal-háromszög oldalai fele olyan hosszúak, mint az eredeti háromszög megfelelő oldalai. Ezért a középvonal-háromszög csúcsait kell súlyozni a szemközti oldalakkal, így pedig a beírt körét kapjuk.
Előzmény: [368] jonas, 2006-02-23 22:29:56

[368] jonas	2006-02-23 22:29:56
Megvan. A középvonal-háromszög beírt körének középpontja lesz, mindjárt elmondom, miért.
Előzmény: [367] jonas, 2006-02-23 22:26:52

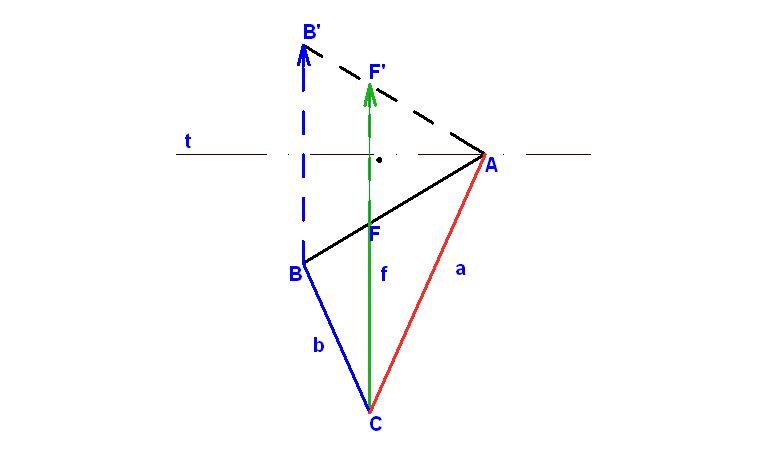
[367] jonas	2006-02-23 22:26:52
Nézzük csak. Nevezetes pont. Egy nagyon hosszú egyenlőszárú háromszögnek a felénél van, tehát nem lehet a magasságpont, a beírt kör középpontja, a súlypont vagy a Feuerbach kör középpontja, csak a körülírt kör középpontja lehetne. Az viszont nyilván nem lehet, mert az a háromszögön kívül is lehet, a drót súlypontja viszont nem. Akkor kevésbé nevezetes pont lesz.
Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11

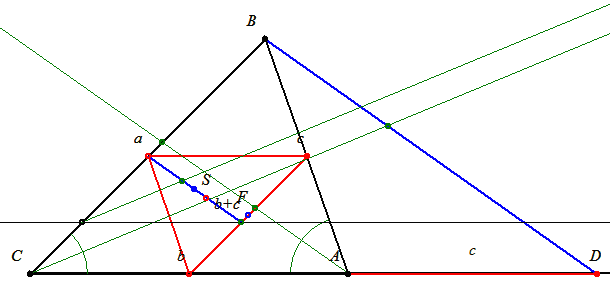
[366] lorantfy	2006-02-23 22:22:21
Szerkesszük meg ezt a speciális súlypontot! Az oldalfelező pontokba helyezzünk az oldalak hosszának megfelelő tömegpontokat. A 'bc' szakaszt c/b arányban kell osztanunk. A szögfelező b/c arányban osztja. Tükrözzük ezt a pontot a szakasz felezőpontjára és helyezzünk ebbe a pontba b+c tömegpontot. Már csak az 'a b+c' szakaszt kell (b+c)/a arányban felosztani. A C-ből induló szögfelező BD szakaszt a/(b+c). Ehhez hasonló kisháromszöget alakítunk ki és ebben a szögfelező azonos arányban osztja a szemközti oldalt. Már csak tükröznünk kell ezt a pontot a felezőpontra. Ez lesz az S súlypont. Remélem idáig jó!

Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11

[365] Hajba Károly

2006-02-23 21:08:51

Jogos. :o)

Drótnak drót, csak nem homogén az én elképzelésem. Egymáshoz viszonyított fajlagos súlyuk arányos az S pont és adott oldal közötti távolsággal.

Visszavonva.

Előzmény: [364] Káli gúla, 2006-02-23 19:19:48

[364] Káli gúla	2006-02-23 19:19:48
A maradék általában nem egyforma széles a három oldalnál.
Előzmény: [363] Hajba Károly, 2006-02-23 18:37:13

[363] Hajba Károly

2006-02-23 18:37:13

66. Tekintsük a teljes ABC $\Delta$ -t és képezzünk egy nála kisebb hasonló $\Delta$ -t úgy, hogy a súlypontjuk egybeessen és az egymásnak megfelelő oldalak rendre párhuzamosak legyenek. A két $\Delta$ közös súlypontja is az S pontban lesz, így elvileg az eredeti $\Delta$ -ünkből elvesszük a kisebb $\Delta$ -t, akkor ennek a "lyukas" $\Delta$ -nek is S marad a súlypontja. Ha növeljük a lyukat, akkor szélső esetben a feladatbali drótvázhoz jutunk.

Így az ABC $\Delta$ -nek is S a súlypontja.

Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11

[362] BohnerGéza	2006-02-23 08:15:11
66. feladat: Hol van egy homogén, vékony drótból készült ABC háromszögnek a fizikai értelemben vett súlypontja? ( ABC-hez kapcsolható nevezetes pont lesz.)

[361] nadorp	2006-02-19 08:52:11
Köszönöm a megoldást. Először én is hasonlóan csináltam, aztán rájöttem, ez a megoldás is a háttérben tulajdonképpen - ahogy Te is írtad az elején - trigonometrikus ( az x<tg x összefüggést használja ), pedig nincs is rá szükség. Legyen a sokszög oldala egységnyi és a beírt kör sugara r. Ekkor K=n, $T=\frac{nr}2$ . Ebből $\frac{K^2}T=\frac{2n}r$ . A beírt kör területe kisebb a sokszög területénél, azaz $r^2\pi<\frac{nr}2$ . Ebböl következik, hogy $\frac{2n}r>4\pi$
Előzmény: [360] qer, 2006-02-17 18:55:53

[360] qer	2006-02-17 18:55:53
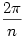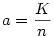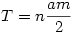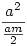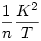Megoldás a 65. feladatra: leírva nincs szögfüggvény, de végülis ott van... Legyen AB az n-szög egyik oldala, a kör sugara egységnyi. Ekkor AOB szög $\frac{2\pi}{n}$ , AB-t jelöljük a-val, OF-t m-mel. Nyílván $a=\frac K n$ , $T=n \frac {am} 2$ . Az $\frac {a^2} {\frac {am} 2}$ hányadost átalakíthatjuk a következő alakra: $\frac 1 n \frac{K^2} {T}$ . 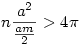Tehát a bizonyítandó egyenlőtlenséget így is írhatjuk: $n\frac {a^2} {\frac {am} 2} > 4\pi$ . 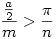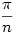Kis átalakítások után a következő alakra hozható az egyenlőtlenség: $\frac {\frac{a}{2}} {m} > \frac \pi n$ . $\frac \pi n$ az AOF (vagy A'OF') szöggel egyenlő. 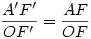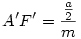Mivel $\frac {A'F'} {OF'} = \frac {AF} {OF}$ , ebből következik (OF'=1), hogy $A'F' = \frac {\frac{a}{2}} {m}$ . Mivel n>2 egész szám ezért, az AOF szög kisebb mint derékszög. Ezért már csak azt kell bebizonyítani, hogy AF' ív kisebb mint A'F'. Mivel AOF' körcikk benne van az A'OF' háromszögben, ezért a területe is kisebb. 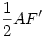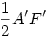A körcikk területe $\frac 1 2 AF'$ (az AF' ívmérték), a háromszögé pedig $\frac 1 2 A'F'$ , azaz igaz az A'F' > AF' egyenlőtlenség. Mivel az átalakítások ekvivalensek voltak ezért igaz a kiinduló egyenlőtlenség is.

Előzmény: [349] nadorp, 2006-02-06 17:30:46

[359] BohnerGéza

2006-02-16 00:11:44

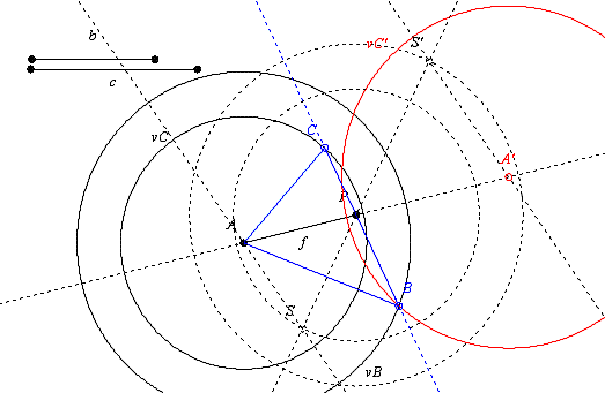
A 64. feladat megoldásához: Vegyük fel például az AP=f szakaszt, az A kp-ú c sugarú kör vonal a B pont számára ( vB ) és a b sugarú pedig a C számára ( vC ). A szögfelező tételtből tudjuk: ha a vC-re alkalmazzuk a P kp-ú lambda = -c/b arányú hasonlóságot, B számára kapunk egy második vonalat (vC'). ( A szerkesztéshez fölhasználunk egy P-től b-re lévő S segédpontot és képét ( S') P-től c-re, SPS' sorrendben. A vC' A' kp-ú c sugarú kör lesz. )

Megjegyzés: Például az AB szakaszból kiindulva B kp-ú lambda=(b+c)/c hasonlósággal is megoldható a feladat P képe lesz C.

[357] Hajba Károly	2006-02-12 18:58:52
Részemről jöhet az arányos szerkesztés nélküli megoldás. Talán a szögfelezők "tétele" C₂ pontjának megszerkesztése a megolodás, de arra még nem jöttem rá, hogy tudom az ismert adatokból megszerkeszteni.
Előzmény: [354] lorantfy, 2006-02-11 20:51:42

[356] lorantfy

2006-02-11 21:31:49

Kedves HoA!

Mindkét megjegyzésed helyénvaló. Köszönet érte! A második még egyszerűbbé teszi a megoldást.

Előzmény: [355] HoA, 2006-02-11 20:56:28

[355] HoA

2006-02-11 20:56:28

Kedves László!

Megoldásod szép és egyszerű. Két megjegyzés:

- az utolsó előtti sorban "A c oldalt felosztjuk a:c arányban" helyett "A c oldalt felosztjuk b:c arányban" a helyes, és így az ábra legalsó "a" betűje helyett is "b" a jó.

- Az AQP $\Delta$ egyenlőszárú volta "ránézésre" is következik abból, hogy két szöge egyenlő, mert f szögfelező , PAC és APQ váltószögek

Előzmény: [352] lorantfy, 2006-02-11 13:12:31

[354] lorantfy

2006-02-11 20:51:42

Köszönöm! Így már világos Nagyon ügyes.

Már csak egy arányos szerkesztés nélküli megoldást várunk!

Előzmény: [353] Hajba Károly, 2006-02-11 19:49:37

[353] Hajba Károly	2006-02-11 19:49:37
Kedves László! Az arányosításnál egy kis magyarázatbeli bakit elkövettem, de a szerkesstés menete szabályos. Felszerkesztettem a Te ábrád szerint újra: t illeszkedik B-re és merőleges f-re. P tükörképe t-re P'. Így az ACP 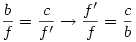$\Delta$ ill. ABP' $\Delta$ hasonlók. AP' $\to$ f.'. $\frac{b}{f}=\frac{c}{f'} \to \frac{f'}{f}=\frac{c}{b}$ . S a szerkesztés menete: Felveszem az f egyenest és felmérem rá AP szakaszt. Elkészítem a 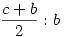$\frac{c+b}{2} : b$ arányosítást f-re. Ez P". Erre a pontra merőlegesen felszerkesztem a t egyenest, majd A-ból rámérem c-t, ez adja a B pontot. Innen már megegyezik a tieddel és nyilvánvaló.

Előzmény: [352] lorantfy, 2006-02-11 13:12:31

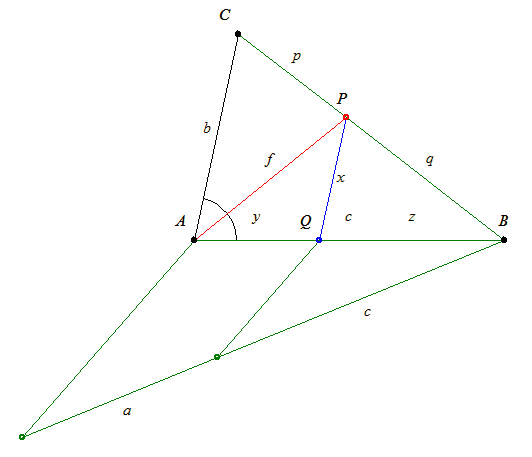
[352] lorantfy	2006-02-11 13:12:31
Kedves Károly! Lehet, hogy jó a megoldásod, de én nem értem a magyarázatot. Fölteszem az enyémet, ez is arányos szerkesztéssel megy. 64. feladat megoldása: Adott az ABC háromszögben a b, c oldal és az f szögfelező. A szögfelező a BC oldalt P pontban metszi. Legyen CP=p és PB=q. A szögfelező tételből következik, hogy 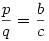$\frac{p}{q} =\frac{b}{c}$ . Húzzunk párhuzamost a P pontból AC-vel, ez az AB oldalt Q pontban metszi. Legyen PQ=x, AQ=y és QB=z. Ekkor a párhuzamos szelők tételéből: 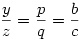$\frac{y}{z}=\frac{p}{q}=\frac{b}{c}$ . 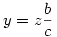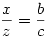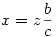Vagyis $y=z\frac{b}{c}$ Másrészt a közbenső szakaszokra, QBP és ABC háromszögek hasonlóságából: $\frac{x}{z}=\frac{b}{c}$ . Vagyis $x=z\frac{b}{c}$ Tehát x=y. Az AQP $\Delta$ egyenlő szárú. A szerkesztés innen már egyszerű. A c oldalt felosztjuk a:c arányban. Q pontból AQ-val, A-ból f-el körözve kapjuk a P pontot. Majd A-ból b-vel körözve BP egyenesből kimetsszük C-t.

Előzmény: [351] Hajba Károly, 2006-02-07 13:12:51

[351] Hajba Károly	2006-02-07 13:12:51
Legyen az ABC $\Delta$ a megoldás háromszöge! Ismert az a, b, f szakasz. Egy kis elméleti megfontolás a megoldás szerkesztéséhez: Tükrözzük a B és F pontokat az f-re merőleges és A-n átmneő t tükörtengelyre! Ekkor a $\frac{F'A}{AC}=\frac{FB}{BC}$ ill. $\frac{a+b}{2b}$ arányosítással megszerkeszthető a $\frac{CF+CF'}{2}$ szakasz. Innen már nem nehéz kitalálni a szerkesztés menetét.

Előzmény: [346] lorantfy, 2006-02-05 13:46:45

[350] nadorp	2006-02-06 17:32:00
Természetesen 65. feladat

[349] nadorp	2006-02-06 17:30:46
64.feladat. Egy szabályos n-szög területe T, kerülete K. Bizonyítsuk be szögfüggvények nélkül, hogy 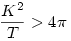$\frac{K^2}T>4\pi$

[348] nadorp	2006-02-06 17:17:45
Negyedik arányos szerkesztés alkalmazása nélküli ( tehát valamilyen direkt ) megoldás engem is érdekelne.
Előzmény: [346] lorantfy, 2006-02-05 13:46:45

Már regisztráltál?
Új vendég vagy?