| [486] Porter | 2006-10-03 13:33:54 |
 Mondjátok csak, olyan opciót bele lehetne építeni valahogy, hogy a program azt is számolja hogy milyen négyzetből hány darabot használt fel???
Mondjuk az 5*6-os téglalphoz kell kettő darab 3*3-as, mag három darab 2*2.
|
|
| [485] Sirpi | 2006-10-03 12:56:30 |
 Jójó tudom, de köszi hogy szóltál :-) 98x99-re így is lefut úgy, hogy nem veszem észre, hogy eltelt volna bármi idő is, de átírom nemsoká, hogy még frappánsabb legyen ;-)
|
| Előzmény: [484] 2501, 2006-10-03 12:49:31 |
|
| [484] 2501 | 2006-10-03 12:49:31 |
 Te gondolom tudod, de azert leirom, hogy ez a gondolatmenet hogyan viheto tovabb.
Mivel a tablazat minden eleme csak a vele azonos sorban elotte, illetve azonos oszlopban folotte levo elemektol fugg, es az elso sor es oszlop, illetve az atlo tartalma trivialis, a tablazat kitoltheto iterativan (rekurzio nelkul).
Meg egy apro eszrevetel (ertsd: kakan is csomot kereses :D) a ciklusokban i-nek nem kell k-1-ig (l-1-ig) mennie, csak a "feleig" (C szintaxissal k/2 vagy k>>1).
|
| Előzmény: [471] Sirpi, 2006-10-02 21:53:21 |
|
|
| [482] jonas | 2006-10-03 11:52:16 |
 Még valami. Mivel úgy adtad fel, hogy "készítsen programot", ezért feltételezem, hogy ez nem matematikai hanem számtech feladat. Ezért aztán jó lenne, ha megmondanád a limiteket a bemenet adataira, mert némelyik Nemes példát azzal tesznek könnyűvé (de becsapóssá), hogy megszorítják a bemenetet.
|
| Előzmény: [479] Sanyi, 2006-10-03 11:09:11 |
|
|
| [480] jonas | 2006-10-03 11:46:37 |
 Igen, ez a fogós feladat még nagyon sok évvel ezelőtt Nemes Tihamér feladat volt. Én akkor, azt hiszem, kilencedikes voltam, de szerintem még tizenkettedikes koromban sem tudtam volna megoldani.
(P.S. Van ennek köze a geometriához?)
|
| Előzmény: [479] Sanyi, 2006-10-03 11:09:11 |
|
| [479] Sanyi | 2006-10-03 11:09:11 |
 Nekem a következő problémám van:
Építőkockákból úgy lehet stabil tornyot építeni, hogy kisebb kockára nem lehet nagyobbat, illetve könnyebb kockára nem lehet nehezebbet tenni. Kezdetben a kockák egy sorban lerakva vannak az asztalon. A soron következő kockát csak egy megépített torony tetejére rakhatjuk, ha kihagyjuk, akkor azt a kockát később sem használhatjuk fel. Készítsen programot, amely adott n kocka alapján megadja a belőlük építhető legmagasabb tornyot! Bemenetként megkapjuk a kockák darabszámát, illetve azt, hogy melyik milyen széles illetve milyen súlyú, és nincs két kocka amelynek a mérete és a súlya is megegyezne.
|
|
| [478] Porter | 2006-10-03 11:05:49 |
 Hűűűűű Köszönöm szépen :)
|
|
| [477] Sirpi | 2006-10-03 09:40:05 |
 A tömb azért kell, hogy ha egyszer egy részeredmény már megvan, akkor azt ne számolja ki a progi újra és újra, mert egyrészt nagy számokra lassú lesz, másrészt ilyenkor a rekurzív hívások miatt egy veremben tárolja, hogy éppen milyen mélységben hívódott meg a rutin, és ilyenkor veremtúlcsordulás esetén a progi szépen fejreáll.
Kicsit kicsinosítottam a progit, a teljes forráskód letölthető innen.
|
| Előzmény: [476] Porter, 2006-10-03 09:25:12 |
|
| [476] Porter | 2006-10-03 09:25:12 |
 már látom miért van ez a mindarabszámos értékadás, mert ugye itt tároljuk a legkisebb j-t.... Ok. A dinamikussá átalakítást még mindig nem vágom. Annak a segítségével meg lehetne adni szebben a mindarabszam értékét?
|
|
| [475] Porter | 2006-10-03 09:01:13 |
 És még egy a programmal kapcsolatabn. Az is jó, ha a mindarabszám nevű változó kezdőértéke nulla, és nem vizsgáljuk h j kisebb-e nála, csak simán eltároljuk benne az értéket? Miért van szükség erre a vizsgálatra???????????
|
|
| [474] Porter | 2006-10-03 08:26:55 |
 Köszönöm a gyors választ Sirpinek. Ki is próbáltam. Nagyon tuti :-)...
Az érdekelne még h pontosan h kell átalakítani dinamikus programmá... Hová építsem be pontosan azt a kétdimenziós tömböt????
|
|
|
| [472] Sirpi | 2006-10-02 22:11:06 |
 Hm, kipróbáltam még pár értéket, próbáljátok megtippelni (programozni nem ér :-P), hogy egy 98x99-es téglalap legkevesebb hány négyzetre vágható fel.
|
| Előzmény: [471] Sirpi, 2006-10-02 21:53:21 |
|
| [471] Sirpi | 2006-10-02 21:53:21 |
 Ez egy sima kétdimenziós dinamikus programozási feladat. C-ben valahogy így néz ki (bocs a tördelésért, de nem nagyon lehet kódot írni ide...):
// ---------------------------------------------
int negyzetekrebont (int k, int l) {
if (k == 1 || l == 1) return (k+l-1);
if (k == l) return 1;
int mindarabszam = 1000000, i, j;
for (i = 1; i < k; i++) { j = negyzetekrebont (i, l) + negyzetekrebont (k-i,l);
if (j < mindarabszam) mindarabszam = j; }
for (i = 1; i < l; i++) { j = negyzetekrebont (k, i) + negyzetekrebont (k,l-i);
if (j < mindarabszam) mindarabszam = j; }
return mindarabszam; }
// ---------------------------------------------
Itt ugye a függvény rekurzívan meghívja önmegát, minden vágást végigpróbálva, egészen addig, amíg 1 szélességű csíkok nem keletkeznek. Nagyobb számoknál a verem hamar betelhet, ezért érdemes egy 2-dimenziós tömböt is csinálni, melyet kezdetben feltöltünk -1 értékekkel, meg ha k=1 vagy l=1, akkor a triviális minimumokkal, és ha valamilyen k,l-re már tudjuk az optimumot, akkor azt nem számoljuk ki rekurzívan újra, hanem beírjuk a tömb megfelelő helyére, és legközelebb csak ki kell onnan olvasni.
Meg is írtam, és próbaképp azt kaptam, hogy 19,23-as téglalapot 9 négyzetre fel lehet vágni.
|
| Előzmény: [470] Porter, 2006-10-02 18:01:28 |
|
| [470] Porter | 2006-10-02 18:01:28 |
 Ebben a problémában várok segítségeket:
Adott egy téglalap alakú fémlap, amit a lehető legkevesebb négyzetre kell darabolni. A darabolásra olyan vágógépet használhatunk, amely csak ketté tudja vágni a lapot valamelyik oldalával párhuzamosan. A keletkezett darabokat külön-külön darabolhatjuk tovább. A téglalap oldalainak hossza egész szám centiméter mértékegységben mérve, és a darabolás eredményeként is olyan négyzeteket kell kapni, amelyek oldalhosszai egész számok. Egy darabolás akkor optimális, ha a lehető legkevesebb négyzet keletkezik.
|
|
|
| [468] HoA | 2006-09-05 11:44:38 |
 Bár néha elmarad a feladatszámozás, vegyük úgy hogy a tied volt a 78-as, én most feladom a 79. feladatot, hátha valaki nem ismeri. Adott az ABC , C-nél 20o -os csúcsszögű egyenlőszárú háromszög. Legyen D a BC szárnak az a pontja, melyre BAD  = 50o , E az AC szárnak az a pontja, melyre EBA = 50o , E az AC szárnak az a pontja, melyre EBA  = 60o . Mekkora szöget zár be az ED egyenes az AB egyenessel? = 60o . Mekkora szöget zár be az ED egyenes az AB egyenessel?
Mivel a feladat a 70-es 80-as években egy KöMaL cikkben példaként szerepelt - ott a megoldás kulcsa az volt, hogy az ábrát a szabályos 18-szög és összes átlói által kifeszített hálózat részeként tekintjük - most legyen az a cél, hogy minél kevesebb új pont felvételével adjunk elemi geometriai megoldást.
|
 |
| Előzmény: [467] rizsesz, 2006-09-05 09:41:19 |
|
| [467] rizsesz | 2006-09-05 09:41:19 |
 Egy újabb remek feladat: adott egy kör alapú henger alakú tortánk, és ezt kellene 12 vágással 80 szeletre (részre) vágni. Semelyik 3 vágás nem mehet át egy ponton, viszont bármelyik kettőnek van közös metszéspontja.
|
|
|
|
|
| [463] jonas | 2006-08-28 19:01:13 |
 76., 77. feladatokra. Ha a töröttvonal egy nagyon lapos egyenlőszárú tompaszögű háromszög, akkor a kört csak egyféleképpen lehet kiválasztani, és a háromszög kerületéhez képest ez akármilyen nagy lehet. Tehár nem igaz az állítás.
|
| Előzmény: [462] Csimby, 2006-08-28 14:46:02 |
|
| [462] Csimby | 2006-08-28 14:46:02 |
 76. feladat
Adott egy h hosszú zárt töröttvonal. igaz-e hogy mindig kiválasztható 3 csúcsa, melyek köréírható köre lefedi az alakzatot és átmérője kisebb/egyenlő mint h/2 (ha nem, akkor mi a legkisebb c konstans amit az 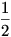 helyére írhatunk). helyére írhatunk).
77. feladat
Van e olyan c konstans, hogy bármely d átmérőjű alakzat lefedhető egy cd átmérőjű körrel. (Mi a legkisebb ilyen c)
Nem tudom milyen nehezek, csak eszembe jutottak.
|
|








 = 50o , E az AC szárnak az a pontja, melyre EBA
= 50o , E az AC szárnak az a pontja, melyre EBA 
