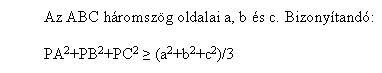| [598] HoA | 2007-01-10 15:51:57 |
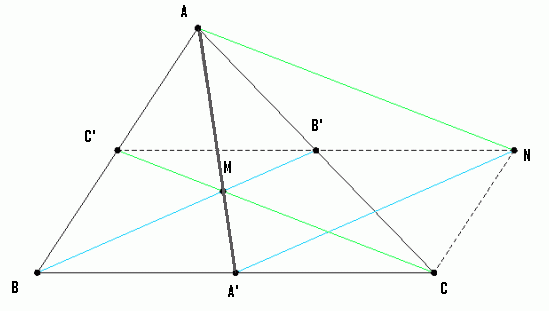
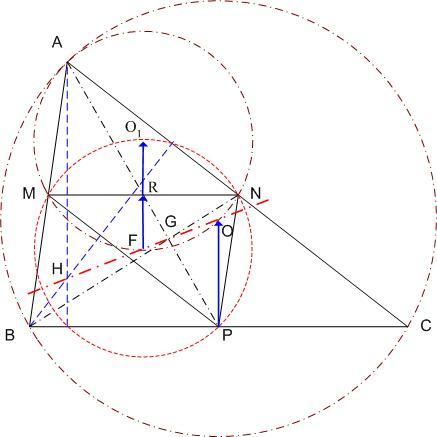
 A bizonyítás, ahol egy 3-as szorzóval elszámoltam magamat :-) : Cckek jelöléseivel ( ha már... ), legyen a körülírt kör középpontja O, a Feuerbach köré F, MN felezőpontja R. ABC  az AMN az AMN  A-ból vett kétszeres nagyítása, így A-ból vett kétszeres nagyítása, így 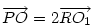 . AMN . AMN  és PNM és PNM  egymás tükörképei R-re, ezért egymás tükörképei R-re, ezért 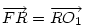 , vagyis , vagyis 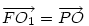 . .
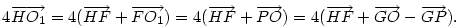 Hasonlóan Hasonlóan 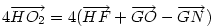 és és 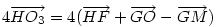 A hármat összeadva A hármat összeadva 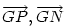 és és 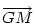 kiesik, mert egy kiesik, mert egy  súlyvonalainak harmadai, így vektorösszegük súlyvonalainak harmadai, így vektorösszegük 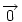 . Igazolandó : . Igazolandó : 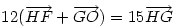 . Legyen az Euler-egyenesen . Legyen az Euler-egyenesen 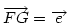 . Ekkor . Ekkor 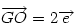 , , 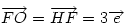 és és 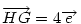 . Egyenlőségünk tehát . Egyenlőségünk tehát 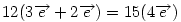 , amit már nem nehéz belátni. , amit már nem nehéz belátni.
|
 |
| Előzmény: [595] HoA, 2007-01-09 11:13:46 |
|
|
|
|
| [594] Cckek | 2007-01-08 21:12:11 |
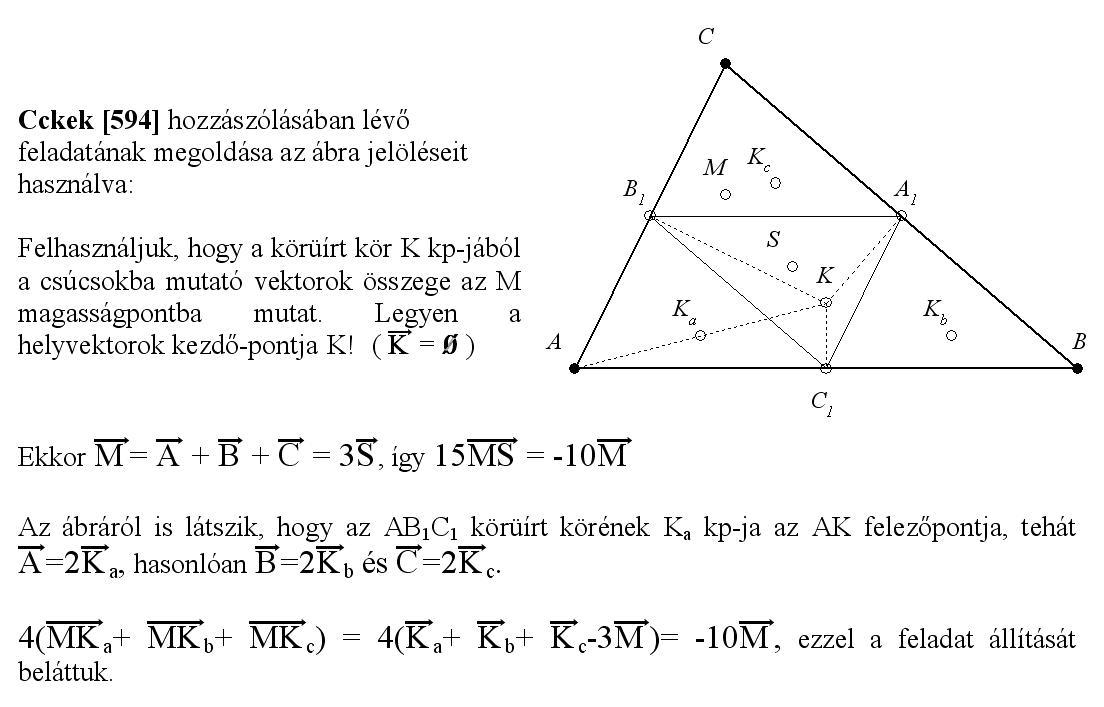
 Legyen G az ABC háromszög súlypontja, H az ortocentruma, M, N, P az AB, AC, BC oldalak felezőpontjai, O1,O2,O3 az AMN, BMP illetve CNP háromszögek köré írt körök középpontjai. Bizonyítsuk be hogy : 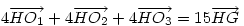
|
|
| [593] HoA | 2007-01-08 15:59:17 |
 Mivel két hete senki sem szólt hozzá, leírok egy megoldást. Nézzük meg, mi a mértani helye a síkban azoknak a pontoknak, melyekre az ABC  csúcsaitól mért távolságok négyzetösszege csúcsaitól mért távolságok négyzetösszege
adott konstans?
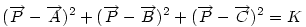
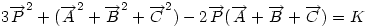 Ha origónak az ABC Ha origónak az ABC  S súlypontját választjuk, S súlypontját választjuk, 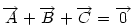 ; ; 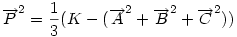 , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha 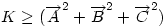 (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor 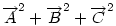 . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De 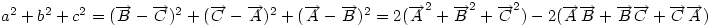 Origó választásunk miatt Origó választásunk miatt 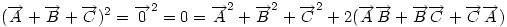 Innen Innen 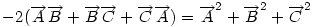 Tehát valóban Tehát valóban 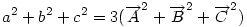
|
| Előzmény: [588] BohnerGéza, 2006-12-25 22:50:17 |
|
| [592] Sirpi | 2007-01-05 16:10:42 |
 Ezt hívják Euler-egyenesnek, és ráadásul az S pont harmadolja (O-hoz közelebb) az OM szakaszt.
Egybe akkor és csak akkor esnek, ha a háromszög szabályos.
|
| Előzmény: [591] Cckek, 2007-01-05 16:04:29 |
|
| [591] Cckek | 2007-01-05 16:04:29 |
 Igaz-e, hogy bármely háromszögben az ortocentrum, a súlypont és a háromszög köré írt kör középpontja kollineárisak? (vagy egybeesnek:)
|
|
|
| [589] HoA | 2006-12-27 10:11:54 |
 BohnerGéza ábrája alapján ha az  , , , , paraméterekkel kifejezett koordinátákra felírjuk az paraméterekkel kifejezett koordinátákra felírjuk az 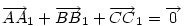 vektoregyenletet, rövid számolás után kapjuk, hogy vektoregyenletet, rövid számolás után kapjuk, hogy  = = = = , vagyis P (Cckek-nél M) = , vagyis P (Cckek-nél M) = 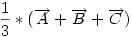 , vagyis M a súlypont. , vagyis M a súlypont.
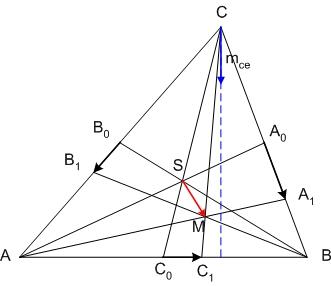
Ha [582] "akkor" ágának bizonyítására elfogadjuk az [586] ábráját, a "csak akkor" ágra itt egy - talán kicsit szemléletesebb - bizonyítás. Legyenek a háromszög oldalfelező pontjai A0,B0,C0 , a súlypont S, továbbá M, A1,B1,C1 [582] szerint. A súlyvonalak a háromszöget hat kis háromszögre osztják. Az általánosság megszorítása nélkül feltehetjük, hogy M a C0BS háromszög belsejében vagy határán van. Mivel pl. 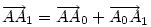 és tudjuk, hogy és tudjuk, hogy 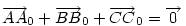 , , 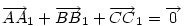 pontosan akkor teljesül, ha pontosan akkor teljesül, ha
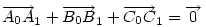 | (1) |
. Ha a három vektor összege 0, akkor tetszőleges irányú vetületüké is az. Tekintsük az mc magasságra vett vetületeket - az mce egységvektorral vett skaláris szorzatokat. Ez 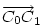 esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így 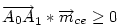 és és 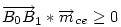 . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S. . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S.
|
 |
| Előzmény: [587] BohnerGéza, 2006-12-25 22:49:35 |
|
|
|
|
| [585] HoA | 2006-12-23 09:19:45 |
 Azt hiszem az ellentmondás feloldása az, hogy Ti szakaszokról beszéltek, a feladat pedig vektorokról szól: az AA1, BB1, CC1 vektorok pontosan akkor alkotnak vektorháromszöget , ha M a súlypont. Lehet, hogy Cckek ezt akarta a szögletes zárójelekkel jelezni.
|
| Előzmény: [584] Cckek, 2006-12-22 21:02:28 |
|
|
| [583] jenei.attila | 2006-12-22 20:21:22 |
 Ezt sajnos nem értem. Azt akarod mondani, hogy ha a súlyponttól csak egy "kicsit különböző" pontot veszünk, akkor a szóbanforgó szakaszokból nem szerkeszthető háromszög? Ezek a szakaszok az M pont megválasztásával nyilván folytonosan változnak, tehát a súlyponttól való kis eltérés a hosszukban is kis változást eredményez. A háromszög egyenlőtlenségbe pedig még biztos hogy belefér egy kis változás. Valamit nyilván félreértek, pontosítanád egy kicsit?
|
| Előzmény: [582] Cckek, 2006-12-22 16:56:49 |
|
| [582] Cckek | 2006-12-22 16:56:49 |
 Legyen M az ABC háromszög egy belső pontja. AM,BM,CM a szemközti oldalakat metsze rendre az A1,B1,C1 pontokban. Bizonyítsuk be, hogy [AA1],[BB1],[CC1] szakaszok akkor és csak akkor egy háromszög oldalai ha M az ABC háromszög súlypontja.
|
|
| [581] Hajba Károly | 2006-11-23 15:30:14 |
 Én sem.
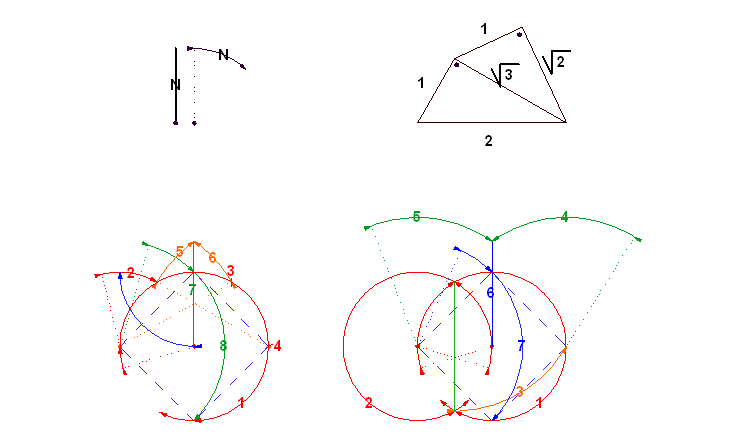
Az [577]-es válaszom után még motoszkált valami a fejemben és elkezdtem firkálgatni (a pitagórászi ábrácskára a köröket, az ábra jobb felső sarkában) és belémcsapot az isteni szikra. :o)
|
| Előzmény: [580] AzO, 2006-11-23 15:06:26 |
|
|
|
| [578] Hajba Károly | 2006-11-22 08:47:12 |
 Csimby!
Nem számoltál még be, hogy mire jutottatok?
---
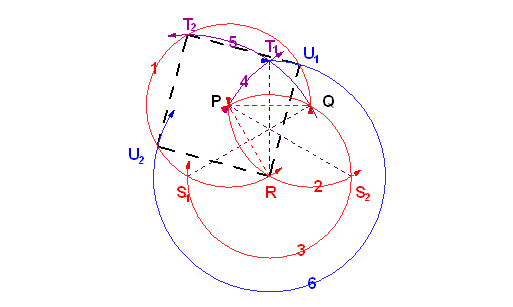
Én közben találtam egy "igaz" 6 körös megoldást, ebben nincs mérés miatti körzőmozgatás:
|
 |
|
| [577] Hajba Károly | 2006-11-22 00:07:35 |
 Én fenn a Gellért-hegyen egy csillagász szakkörön hallottam és főleg a középiskolásoknak adták föl, én ott csak vízhordó voltam. :o)
Szóval a szakkörvezető így kezdte: Már az ókori görögök is ...
A definició, najó legyen csak "definició" szerint ScarMan megoldása valóban 7 körző-felemeléses, mert a 3. lépés távolságát használja fel a 4. és 5. lépésben. Lásd az ábrámat, melyen az én megoldásomat és az övét is felszerkesztettem.
Értelmező ábrácska a bal felső fekete, vastag vonal: mérés, nyilazott ív: körzőzés.
ScarMan-nak meg még egy grat.
|
 |
| Előzmény: [576] AzO, 2006-11-21 23:10:25 |
|
| [576] AzO | 2006-11-21 23:10:25 |
 Az 1977-es feladatot nem Napoleon-feladat-nak hivjak? Mintha olvastam volna valahol mostanaban. A definiciomert nem vallalok felelosseget, mert csak emlekezetbol mondtam, es akkor az en 7 lepeses megoldasom is mar 8 :)))
|
| Előzmény: [575] Hajba Károly, 2006-11-21 08:33:01 |
|
| [575] Hajba Károly | 2006-11-21 08:33:01 |
 Üdv a körösöknek! és grat ScarMan-ek is!
Nem kekeckedni szeretnék, de AzO definiciója szerint - körző felvétele a lépés vége - csak 8 lépésből lehet megszerkeszteni. Az alább közöltem megoldás 7 körzőzés és 1 mérés, ScarMan-nek 6 körzőzés és 2 mérés. S gyanítom, hogy a feladatban nem véletlen volt 8 lépés kitűzve, főleg ELTE matekon.
Mellesleg alább -habár gyanítom nem eléggé értelmezhető módon- az én megoldásom is ott van. Volt ez pár éve kérdés az "Éredekes matekfeladatok"-ban, akkor megoldottuk, ha jól emlékszem, Jenei Attila adta a másik megoldást. (4.1, ill. 4.2)
Az akkori megoldásomban a két adott pont a négyzet két sarokpontja, ehhez +1 körzőzés kell, de így szerintem más sem tudja rövidebben, míg az eddig megismert egyéb megoldásnál az egyik pont nem a négyzet sarokpontja, hanem a közepe. Ezt szerkesztette meg korábban J. A.
Én anno 1977-ben így hallottam a feladatot: Osszunk négy egyenlő részre egy körívet csak körző használatával! (Akkor 8-ikos koromban a feladat győzött. :o) Ez -a fenti definíció szerint- 7 lépésből megoldható, mivel adott volt már egy körív.
|
| Előzmény: [574] AzO, 2006-11-20 22:59:09 |
|
| [574] AzO | 2006-11-20 22:59:09 |
 Szerintem is 6 lepes. Grat! :)
|
|



 az AMN
az AMN 



 ,
, ,
, paraméterekkel kifejezett koordinátákra felírjuk az
paraméterekkel kifejezett koordinátákra felírjuk az