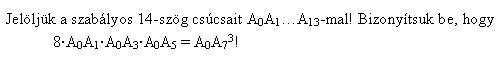| [661] trizi | 2007-02-28 15:17:12 |
 epsilon! már meg is van az eredmény, köszi
|
|
| [660] epsilon | 2007-02-28 14:17:06 |
 Bizonyára tudod, hogy a körszelet területe T=r×r×(x-sinx)/2. Legyen O a kőr középpontja, AB a 210 cm hoszú húr, és legyen OM merőleges az AB húrra, M a talppont az AB húron. Legyen r a kör sugara, így pl. az OAB derékszögü háromszögben az átfogó r, a két befogó 105 illetve (r-50). Pitagorász tételével innen kijön az r. Továbbá az OAB háromszög területét 2 féle képpen felírjuk: 1/2×AB×OM=1/2×OB×OC×sinx vagyis 210×(r-50)=r×r×sinx és innen az r ismeretében megvan sinx és aztán x is.
|
|
| [659] trizi | 2007-02-28 12:36:49 |
 Sziasztok. Tud valaki segíteni körszelet területének kiszámításában, ha m=50 cm h=210 cm és más adatot nem ismerek?
|
|
| [658] jenei.attila | 2007-02-27 14:59:55 |
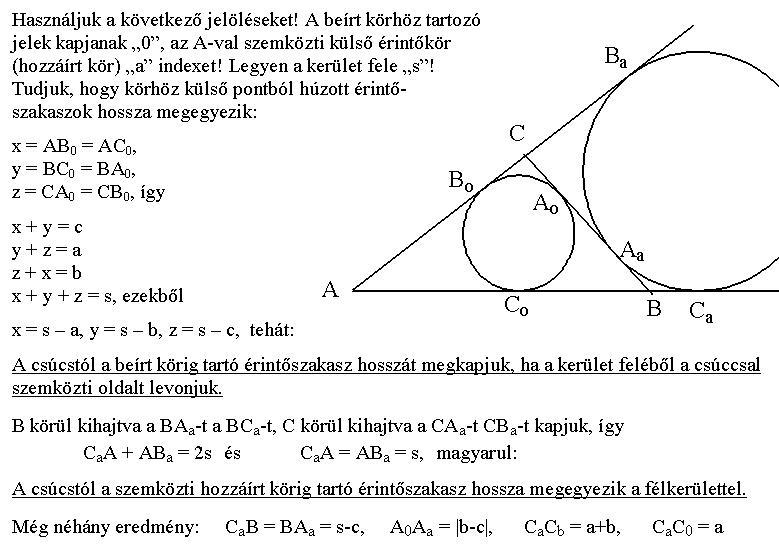
 A feltételből következik, hogy a szemközti oldalak hosszának összege egyenlő. Mivel konvex négyszögről van szó, ezért a négyszög érintő négyszög. Érintő négyszögben az egyik átló behúzásával keletkező két háromszög beírt körei érintik egymást. Ez csak vázlat, de nagyon könnyű bizonyítani ezeket az állításokat.
|
| Előzmény: [653] Csimby, 2007-02-23 01:20:45 |
|
| [657] HoA | 2007-02-26 16:03:28 |
 Javaslom 107. feladat nak [656] általánosítását: Bizonyítsuk be, hogy egy sokszöglapon két pont távolsága (a pontok a határon is lehetnek) nem lehet nagyobb, mint a sokszög két, egymástól legtávolabbi csúcsának távolsága.
|
| Előzmény: [656] fermel, 2007-02-25 13:01:40 |
|
| [656] fermel | 2007-02-25 13:01:40 |
 A 638-asban leírt feladattal kapcsolatban lenne még kérdésem. Azt kellene belátni, hogy egy 2x2-es házikóban(2x1-es téglalapon egy 2 alapú, 1 magasságú egyenlőszárú háromszög)két pont távolsága maximum négyzetgyök 5.(természetesen a pontok a határon is lehetnek) Köszönöm: fermel
|
| Előzmény: [638] fermel, 2007-02-17 14:42:37 |
|
|
|
| [653] Csimby | 2007-02-23 01:20:45 |
 106.feladat Egy konvex négyszög egyik átlóját behúzva, a kapott két háromszög beírható körei érintik egymást. Bizonyítsuk be, hogy a másik átlót behúzva ugyanez igaz. (Ma volt Arany Dani feladat 9.oszt.-osoknak)
|
|
| [652] BohnerGéza | 2007-02-23 00:42:22 |
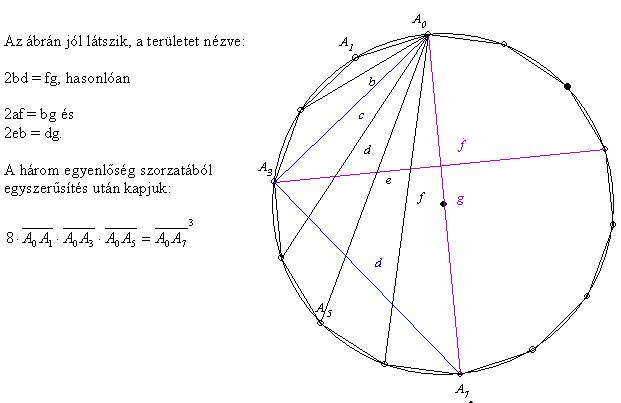
 Köszönöm nadorp [642] tanulságos megoldását! Azt hiszem, ez és az alábbi alapján is kitalálhatunk új feladatokat.
A feladatra a B.3970 ([632]-ben is megtalálható) megoldásának keresése közben találtam, egy átmérő behúzása után a következőt észrevéve:
|
 |
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [648] HoA | 2007-02-22 15:52:27 |
 Nagyon szép megoldás!
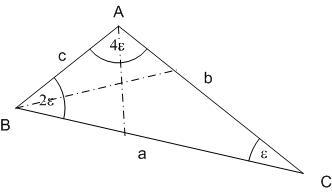
Azért leírom, szerintem mire gondoltak a feladat kitűzöi. Tekintsük a szabályos hétszög oldala és két különböző átlója által alkotott ABC  -et . -et . 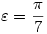 , ,  =4. =4. , , =2. =2. , , = = . Vegyük észre, hogy mind az . Vegyük észre, hogy mind az  mind a mind a  szög felezője a szög felezője a  -et egy, az eredetihez hasonló és egy egyenlőszárú -et egy, az eredetihez hasonló és egy egyenlőszárú  -re bontja. Az elsőből -re bontja. Az elsőből 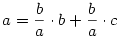 , a2=b2+bc , a másodikból , a2=b2+bc , a másodikból 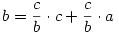 , b2=c2+ac . Felhasználva, hogy c=1 , b2=c2+ac . Felhasználva, hogy c=1
(1) -ben a-t (2) -ből helyettesítve: (b+1)2.(b-1)2=b2+b=b.(b+1)
| a+b=(b+1)(b-1)+(b+1)(b-1)2=(b+1)(b-1)(1+b-1)=(b+1)(b-1)b | (5) |
végül
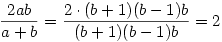 | (6) |
|
 |
| Előzmény: [646] BohnerGéza, 2007-02-22 11:51:37 |
|
|
| [646] BohnerGéza | 2007-02-22 11:51:37 |
 A Ptolemaiosz-tétel szerint a négyszög átlói és oldalai közt igaz, hogy e*f <= a*c+b*d, ahol az egyenlőség húrnégyszögben és csak abban igaz.
Az ABCDEFG szabályos hétszög esetén alkalmazzuk a tételt pl. az ACDE négyszögre, ekkor e*f = a*e+a*f ahonnan az állítás következik.
|
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [645] lorantfy | 2007-02-22 08:38:32 |
 Szia Laura!
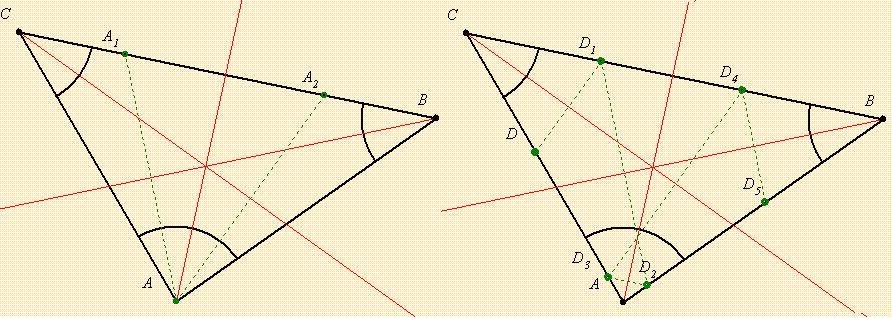
A három szögfelező kevés, kell még egy pont is.
Ha az adott pont mondjuk az A csúcs, akkor tükrözve a másik két szögfelezőre, mindkét pont a BC oldalra esik.Ezt meghúzva megvan B és C.
Ha egy D kerületi pont van megadva, akkor sorra tükrözzük a három szögfelezőre, addig, míg minden oldalon 2-2 pontot kapunk.
|
 |
| Előzmény: [644] lauraa, 2007-02-21 19:07:11 |
|
| [644] lauraa | 2007-02-21 19:07:11 |
 sziasztok! nem tudja valaki, hogyan lehet megszerkeszteni egy 3szöget, ha adott 3 szögfelezője? köszi előre :-)
|
|
| [643] HoA | 2007-02-21 00:48:30 |
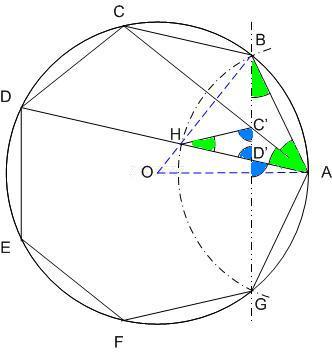
 Egy megoldás [619] mintájára: A szabályos hétszögnek 7 rövidebb és 7 hosszabb átlója van, ezek harmonikus közepe megegyezik egy rövidebb és egy hosszabb átló harmonikus közepével. Tekintsük az egységnyi oldalú ABCDEFG szabályos hétszög AC és AD átlóját. Azt kell igazolni, hogy 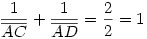 Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara Legyen a hétszög körülírt köre k1, az inverzió k2 alapkörének középpontja A, sugara 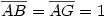 . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H. . Mivel k1 átmegy A-n, inverze a BG egyenes, így C és D C' ill. D' képe is ide esik. Legyen AD és k2 metszéspontja H. 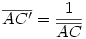 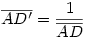 . Bizonyítandó: . Bizonyítandó: 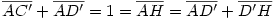 , vagyis elég megmutatni, hogy , vagyis elég megmutatni, hogy 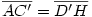 . Az ábrán zölddel jelölt ABG, BAC és CAD szögek . Az ábrán zölddel jelölt ABG, BAC és CAD szögek 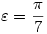 nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC' nagyságúak, mert egy szabályos hétszög körülírt körében az oldalakhoz tartozó kerületi szögek. ABC'  egyenlőszárú, egyenlőszárú, 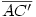 = = 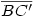 . AC a BAH középponti szög felezője, így BH felező merőlegese, . AC a BAH középponti szög felezője, így BH felező merőlegese, 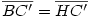 . AC'H . AC'H  egyenlőszárú, AHC' szög = egyenlőszárú, AHC' szög =  . C'D'H . C'D'H  = AD'G = AD'G  = 3 = 3 mint az ABD' mint az ABD'  külső szöge. De ekkor a HC'D' külső szöge. De ekkor a HC'D'  -ben a HC'D' -ben a HC'D'  = = -4. -4. =3. =3. , HC'D' , HC'D'  egyenlőszárú, egyenlőszárú, 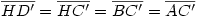 , amit igazolni akartunk. , amit igazolni akartunk.
|
 |
| Előzmény: [636] BohnerGéza, 2007-02-12 22:00:07 |
|
| [642] nadorp | 2007-02-19 08:51:18 |
 Ha a szabályos 14-szöget egységnyi sugarú körbe írjuk, akkor nyilván elég belátni, hogy A0A1.A0A3.A0A5=1. Legyen x az első 14-dik komplex egységgyök. ( nem akarok  -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt
A=A0A1.A0A3.A0A5=|x-1||x3-1||x5-1|=|(x-1)(x8-x3-x5+1)|=(x-1)(-x-x3-x5+1)|
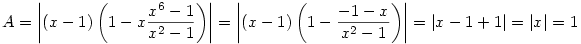
|
| Előzmény: [639] BohnerGéza, 2007-02-18 00:54:57 |
|
|
|
|
| [638] fermel | 2007-02-17 14:42:37 |
 Egy kombinatorikai feladat megoldásában szeretném a segítségeteket kérni. Azért ide írom, mert a probléma végül is geometriai. Adott egy 3x4-es téglalap. Bizonyítsuk be, hogy bárhogyan is adunk meg benne 6 pontot, biztos, hogy található köztük kettő, melyek távolsága nem nagyobb , mint négyzetgyök 5! A feladat 7 pont esetén nagyon egyszerű. Felosztjuk a téglalapot 6 db 2x1-es téglalapra. Ez 6 skatulya. 7 pont közül biztosan van legalább kettő, amelyik ugyanabba a skatulyába tartozik, azon belül pedig a maximális távolság valóban négyzetgyök 5. Megfelelő skatulyák megválasztásával már 6 pontra is igaz. Sajnos nem találom az 5 részre való felosztás módját. Köszönöm a segítséget. (Elnézést a négyzetgyök 5 kezdetleges írásmódjától, de hiába írtam be Worldben jól, nem másolta át nekem ide.)
fermel
|
|
|








 -et .
-et .  =4.
=4. ,
, =2.
=2. =
=


 = AD'G
= AD'G  -4.
-4.
 -t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt
-t írni, mert akkor túl sokat kéne gépelni -:). Ekkor x7=-1 miatt