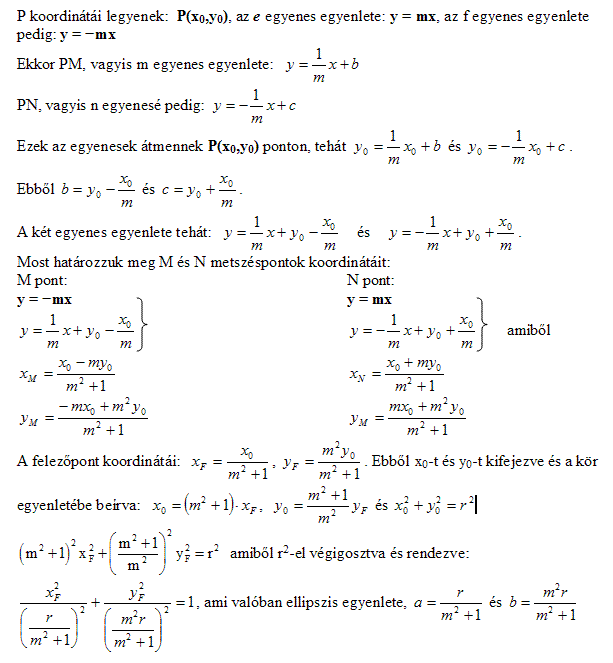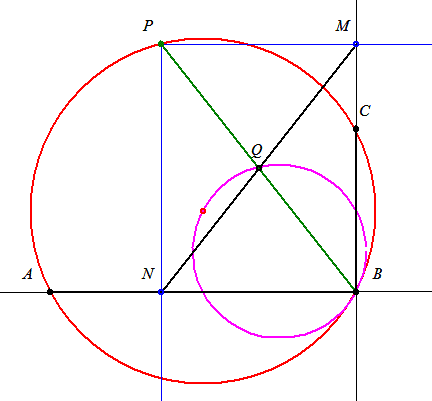| [788] Sirpi | 2007-06-24 09:23:44 |
 Hm, ez izgalmasabban hangzik, de erre a részére egyelőre nem tudom a megoldást. Viszont mivel az eredeti kérdésre jó pár napja beírtam az eredményt, és így mindenkinek volt ideje picit gondolodni rajta, aki akart, ezért írok hozzá egy megoldásvázlatot is (tényleg csak vázlat, nem bizonyítok benne minden apró részletet):
Két dolgot kell bizonyítani:
a) 3 gömb nem elég
Illesszünk síkot a 3 gömbközéppontra, majd a fényforrásban állítsunk merőlegest erre a síkra. Ennek az egyenesnek az a fényforrásból kiinduló nyílt félegyenese, amelyik nem metszi a síkot, nyilvánvalóan nincs eltakarva (mert ha bármelyik pontja része lenne valamelyik gömbnek, akkor maga a fényforrás is).
b) 4 már elég
Helyezzük bele a fényforrást egy tetraéder belsejébe. Ha most minden lapot eltakarunk a fényforrás szemszögéből, akkor készen is vagyunk. Arra kell csak vigyázni, hogy ezek a gömbök ne metsszék egymást, de ez a gömbök megfelelő eltávolításával és ezzel arányos megnagyobbításával megtehető (egymás után tesszük le a gömböket és mindegyiket úgy távolítjuk-nagyítjuk középpontos hasonlósággal a fényforrásból, hogy távolabbra kerüljön, mint a lefedendő térszögbe belógó más gömbrészek).
|
| Előzmény: [785] Cckek, 2007-06-20 16:13:21 |
|
| [787] lorantfy | 2007-06-22 15:26:24 |
 Szia HoA!
Persze, jól gondolod.
A Word-höz van MathType egyenletszerkesztőm, azzal jóval gyorsabban lehet egyenleteket írni, mint TeX-ben.
Mikor készen van kifényképezem a vágólapra Print Screen-nel aztán Paint-ben gif formátumban elmentem.
Még átlátszóvá lehetne tenni, akkor feltöltve a sárga háttérre és nem lenne keretes.
|
| Előzmény: [786] HoA, 2007-06-22 09:58:39 |
|
|
|
|
|
| [782] Cckek | 2007-06-18 21:42:27 |
 Modosítok. A gömbök diszjunktak természetesen.
|
|
|
|
| [779] Cckek | 2007-06-18 18:28:14 |
 Legalább hány gömb képes teljesen leárnyékolni egy pontszerű fényforrást? (a fényforrás nem lehet a gömbök belsejében)
|
|
| [778] HoA | 2007-06-18 16:31:00 |
 Az előző hozzászólás utolsó mondatai természetesen úgy értendők, hogy itt Q nem az ellipszis pont, hanem az F - ből e-re bocsátott merőleges és a Thálesz-kör metszéspontja.
|
| Előzmény: [777] HoA, 2007-06-18 16:25:53 |
|
| [777] HoA | 2007-06-18 16:25:53 |
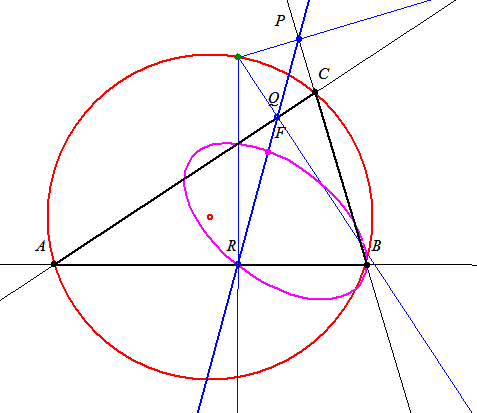
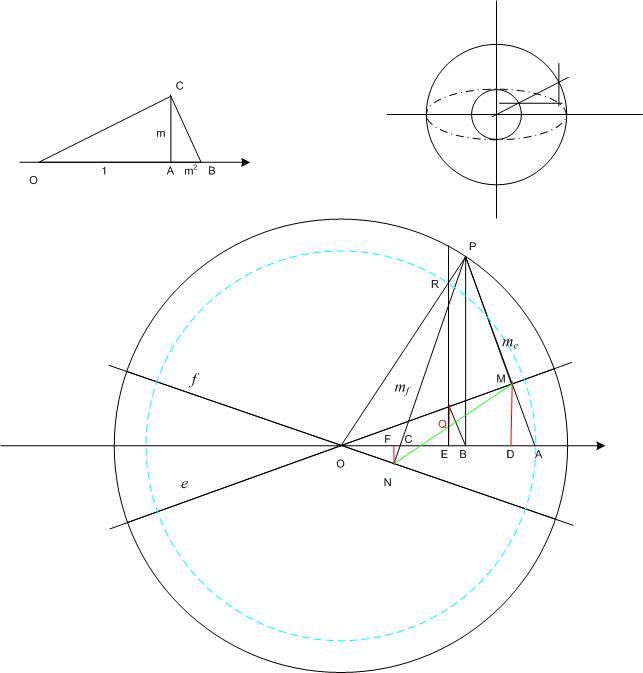
 116.és117.feladat: Két "segédtétel" : 1) Az x tengely B pontjából merőlegest bocsátunk az O-n átmenő m meredekségű egyenesre, a talppont legyen C. C merőleges vetülete az x tengelyre A. Ekkor 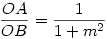 . Jelöljük ezt az arányt q-val. 2) Tekintsük ismertnek az alábbi ellipszis pontokat eredményező eljárást: A közös O középpontú k1 és k2 köröket metsző O-n áthaladó e egyenest O körül forgatjuk, a körökkel alkotott metszéspontok P1 ill. P2. A P1-n át az y tengellyel és P2-n át az x tengellyel párhuzamos egyenesek metszéspontja Q. Belátható, hogy az így adódó Q pontok egy ellipszisen találhatók. . Jelöljük ezt az arányt q-val. 2) Tekintsük ismertnek az alábbi ellipszis pontokat eredményező eljárást: A közös O középpontú k1 és k2 köröket metsző O-n áthaladó e egyenest O körül forgatjuk, a körökkel alkotott metszéspontok P1 ill. P2. A P1-n át az y tengellyel és P2-n át az x tengellyel párhuzamos egyenesek metszéspontja Q. Belátható, hogy az így adódó Q pontok egy ellipszisen találhatók.
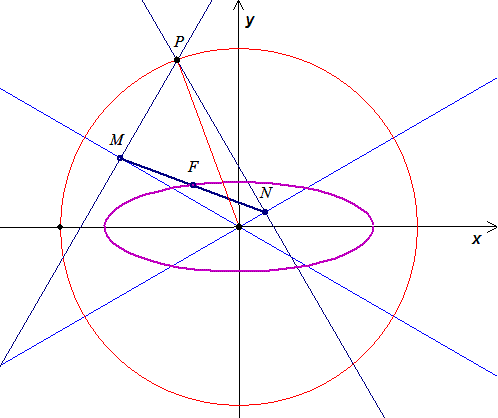
Eredeti feladatunk r sugarú k körének P pontjából az O-n átmenő 0<m<1 meredekségű e egyenesre bocsátott me egyenes talpponja legyen M, az x tengellyel alkotott metszéspontja A. A P-ből a -m meredekségű f egyenesre bocsátott mf egyenes talpponja legyen N, az x tengellyel alkotott metszéspontja C. P merőleges vetülete az x tengelyen B. APC  egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen. egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.
Q -nak az y tengelyre vett vetületét vizsgálva hasonló eredményre jutunk, csak ott az 1. segédtétel szerint fellépő meredekség m helyett 1/m, így az adódó kicsinyítési arány 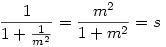 . Q rajta van az OP egyenes és az O középpontú, sr sugarú kör S metszéspontjából az y tengelyre bocsátott merőlegesen. A Q pontok tehát a 2. segédtételben leírt ellipszis pontjai, ahol a generáló körök sugarai ( az ellipszis tengelyei ) qr illetve sr. . Q rajta van az OP egyenes és az O középpontú, sr sugarú kör S metszéspontjából az y tengelyre bocsátott merőlegesen. A Q pontok tehát a 2. segédtételben leírt ellipszis pontjai, ahol a generáló körök sugarai ( az ellipszis tengelyei ) qr illetve sr.
[775] ábráján a T pont az OEP derékszögű  -ben éppen az 1. segédtételben leírt módon jön létre, tehát OT = qr = a. Mivel q+s =1, TE = OE - OT = r ( 1 - q ) = sr = b. -ben éppen az 1. segédtételben leírt módon jön létre, tehát OT = qr = a. Mivel q+s =1, TE = OE - OT = r ( 1 - q ) = sr = b.
Az f-re vonatkozó állítás téves: Legyen a [775] ábráján OE és FQ metszéspontja U. Nem QU, hanem QO lesz f-el egyenlő. Bizonyítás: Az egységsugarú OE körben 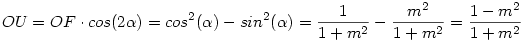 , ahol , ahol  az m meredekségű egyenes irányszöge. Az OQE derékszögű az m meredekségű egyenes irányszöge. Az OQE derékszögű  -ben OQ OU és OE = 1 mértani közepe, vagyis -ben OQ OU és OE = 1 mértani közepe, vagyis 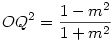 . Másrészt az ellipszisben f2=a2-b2, esetünkben . Másrészt az ellipszisben f2=a2-b2, esetünkben 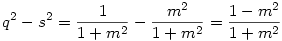 . Tehát f2=OQ2 ; f = OQ . Tehát f2=OQ2 ; f = OQ
|
 |
| Előzmény: [775] BohnerGéza, 2007-06-17 22:24:45 |
|
| [776] lorantfy | 2007-06-18 14:46:29 |
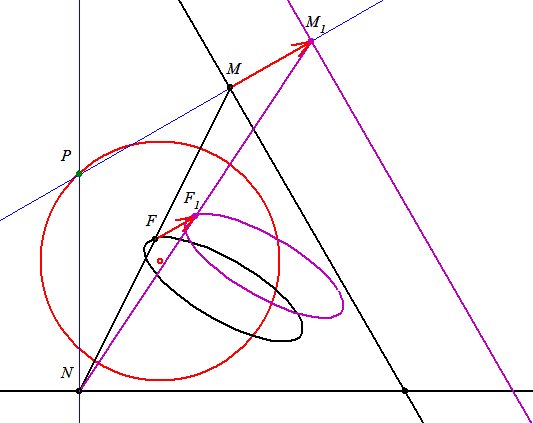
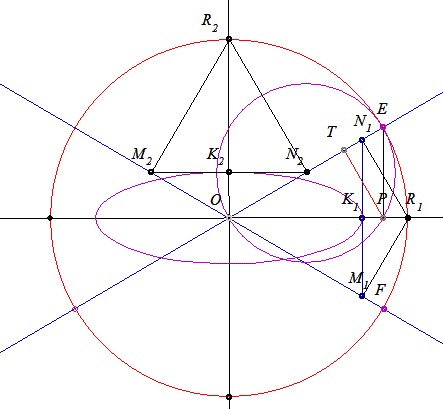
 Az ellipszis nagytengelyét r sugarú körnek az x tengellyel való R1 pontból az e és f egyenesekre bocsájtott merőlegesek talppontjait összekötő szakasz K1 felezőpontjának O-től való távolsága adja. Tehát a nagytengely OK1.
A kistengelyt hasonlóan az R2 pontból származtatva OK2 adja.
A Thálesz-körben lévő OEP háromszög egybevágó az OR1N1 és az OR2N2 háromszögekkel, mert szögeik megegyeznek és átfogójuk r hosszú. Tehát megfelelő részháromszögeik is egybevágóak.
Így az ellipszis nagytengelye: a=OK1=OT, kistengelye: b=OK2=TE. Tehát r=a+b.
|
 |
| Előzmény: [775] BohnerGéza, 2007-06-17 22:24:45 |
|
| [775] BohnerGéza | 2007-06-17 22:24:45 |
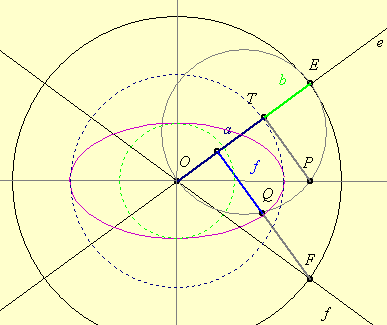
 117. feladat: Használjuk föl, hogy a 116. feladat mértani helye ellipszis! Bizonyítsuk, hogy ennek két (fél)tengelye és a (fél)fókusztávolság megszerkeszthető az ábrán látott módon! ( A [774]-es hozzászólás számolási eredményeinek használata nem szükséges! )
A két adott egyenes e és f, az adott kör sugara egyenlő az ábra OE szakaszával. Válasszuk úgy a jelöléseket, hogy az FOE szög ne legyen nagyobb derékszögnél, messe az OE Thálesz-köre FOE szögfelezőjét P-ben. A P-ből e-re állított merőleges talppontja T. Tehát igazolandó, hogy a=OT, b=TE, valamint az F-ből e-re állított merőleges szakasznak a Thálesz-körbe eső része f!
|
 |
|
|
|
|
|
|
| [769] lorantfy | 2007-06-11 21:08:34 |
 Nézzünk először egy spec. esetet. Amikor a két egyenes, AB és BC merőlegesek egymásra. Ekkor a talppontok felezőpontja egyben PB szakasz felezőpontja is. Igy a keresett mértani hely a kör B középpontú felére kicsinyített képe.
|
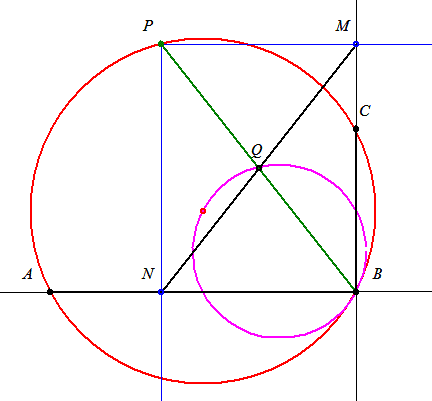 |
| Előzmény: [767] BohnerGéza, 2007-06-06 22:32:11 |
|
|
| [767] BohnerGéza | 2007-06-06 22:32:11 |
 Nagyon szép észrevétel, de mielőtt valaki összekapcsolná a Simson-egyenessel:
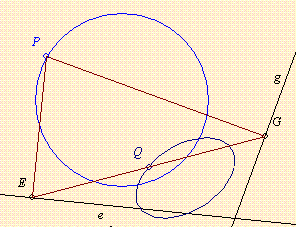
klevente feladata, 116. feladat: Adott egy kör és két egyenes. A kör P pontjából állítsunk merőlegest az egyenesekre, a talppontok közti felezőpont legyen Q. Bizonyitandó, a Q pontok mértani helye ellipszis, ha P végigfut a körön.
|
| Előzmény: [765] klevente, 2007-06-06 14:17:45 |
|
|
| [765] klevente | 2007-06-06 14:17:45 |
 Egy háromszög köré írt kör tetszőleges P pontjából állítsunk merőlegeseket a háromszög oldalegyeneseire. Közismert, hogy ezen merőlegesek talppontjai kollineárisak, ez az ún. Simson-egyenes.
Vizsgáljuk valamelyik két talppont összekötő szakasza felezőpontjának mértani helyét, ha P befutja a köréírt kört. A GeoGebra programmal nézve ez szinte bizonyosan ellipszis.
Kérdések: a) tud-e valaki arról, hogy ez a tény (sejtés) ismertnek számít-e a matematikában? b) tudná-e valaki bizonyítani vagy cáfolni?
Koncz Levente
|
|
| [764] HoA | 2007-05-31 22:11:09 |
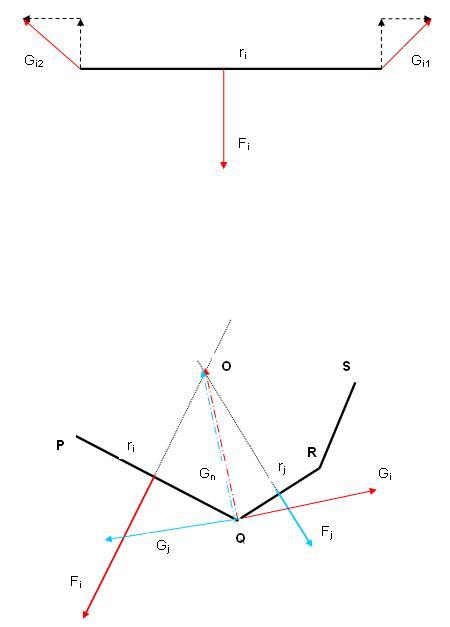
 114** feladat Vizsgáljuk az li hosszúságú ri rúdra ható erőket. A rúdra hat a feladatban adott Fi külső erő és a csuklókban a szomszédos rudak Gi1 és Gi2 kényszerereje. Bontsuk fel az erőket rúdirányú és a rúdra merőleges összetevőkre. Gi1 és Gi2 rúdirányú összetevői egymás ellentettjei, mert a rúd nyugalomban van és más rúdirányú erő nem hat rá. Gi1 és Gi2 rúdra merőleges összetevői egyenlőek és 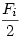 nagyságúak, mert a rúd másik végére vonatkozó nyomatékuk li karon egyensúlyt tart Fi erő nagyságúak, mert a rúd másik végére vonatkozó nyomatékuk li karon egyensúlyt tart Fi erő 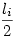 karon kifejtett nyomatékával. Megállapíthatjuk tehát, hogy Gi1 és Gi2 egyenlő nagyságűak. Mivel a csuklókban a rudak azonos nagyságú erővel hatnak egymásra, a szomszédos rúdra hatő kényszererő is akkora, mint Gi1 és Gi2 és így tovább : az összes csuklóban ugyanakkora erők hatnak. Legyen ennek az erőnek a nagysága G. karon kifejtett nyomatékával. Megállapíthatjuk tehát, hogy Gi1 és Gi2 egyenlő nagyságűak. Mivel a csuklókban a rudak azonos nagyságú erővel hatnak egymásra, a szomszédos rúdra hatő kényszererő is akkora, mint Gi1 és Gi2 és így tovább : az összes csuklóban ugyanakkora erők hatnak. Legyen ennek az erőnek a nagysága G.
Tekintsük a szomszédos, li és lj hosszúságú ri és rj rudakra ható erőket. Válasszuk úgy az ábrán az erő mértékegységét, hogy a rúd hosszával arányos Fi és Fj erőket éppen li és lj hosszú vektorral ábrázoljuk. Az ri rúdra a Q csuklóban ható Gi erő rúdra merőleges összetevője Fi/2=li/2 . Rajzoljuk meg Q-ban a sokszög belseje felé mutató, Gi-re merőleges, G hosszúságú Gn vektort, Gi 90 fokos elforgatottját. Ennek ri irányába eső összetevője li/2, tehát O végpontja rajta van ri felező merőlegesén. De a Gn vektort úgy is tekinthetjük, mint az rj rúdra Q-ban ható Gj erö -90 fokos elforgatottját. Mivel Gj erö rj -re merőleges összetevője lj/2 nagyságú, Gn -nek rj irányába eső összetevője is ekkora, vagyis O rajta van rj felező merőlegesén is. Vagyis a P,Q,R pontok egy G sugarú körön vannak. A gondolatmenetet a következő R csuklóra alkalmazva azt kapjuk, hogy a Q,R, S pontok is egy G sugarú körön vannak. A két kör azonos: középpontjuk QR felező merőlegesén a sokszög belseje felé Q-tól és R-től G távolságra lévő O pont. Az eljárást folytatva adódik, hogy a csuklók húrsokszöget alkotnak.
|
 |
| Előzmény: [747] BohnerGéza, 2007-05-23 00:28:23 |
|







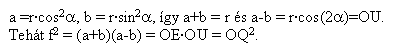

 egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.
egyenlőszárú, magassága PB, így OB = (OA + OC)/2. Ha M x tengelyre merőleges vetülete D, N-é F és az MN szakasz Q felezőpontjáé E, az 1. segédtétel szerint OF=q.OC, OD=q.OA, így OE=(OD+OF)/2=q.(OA+OC)/2=q.OB. QE és OP metszéspontja legyen R. OR=q.OP, Q rajta van az OP egyenes és az O középpontú, qr sugarú kör R metszéspontjából az x tengelyre bocsátott merőlegesen.  az m meredekségű egyenes irányszöge. Az OQE derékszögű
az m meredekségű egyenes irányszöge. Az OQE derékszögű