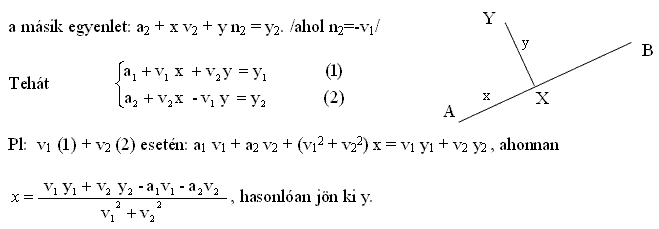|
| [864] jonas | 2007-10-02 16:57:08 |
 Nézzünk egy példát.
Vegyük azt a háromszöget, aminek a csúcsainak koordinátái
x0=(1.4941,0.1445,0.9198)
x1=(1.3248,-0.6318,-0.7830)
x2=(-1.2714,-1.3181,1.8189)
Ekkor az oldalak vektorai
v0=x1-x2=(2.5962,0.6863,-2.6019)
v1=x2-x0=(-2.7655,-1.4626,0.8991)
v2=x0-x1=(0.1693,0.7763,1.7028)
Most számoljuk ki az oldalak által bezárt szögeket az oldalvektorok skalárszorzatából.
|v1|=3.25512
|v2|=1.87908
(v1,v2)=-0.0726366
cos ( - - 0)=(v1,v2)/(|v1|.|v2|)=0.0118753 0)=(v1,v2)/(|v1|.|v2|)=0.0118753
 - - 0=1.58267 0=1.58267
 0=1.55892 0=1.55892
Hasonlóan
 1=1.05618 1=1.05618
 2=0.52649 2=0.52649
Ebből
sin (2 0)=0.0237489 0)=0.0237489
stb, amiből a körülírt kör középpontjába mutató vektor
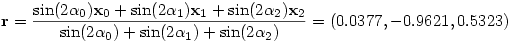
Ennek a távolsága valóban minden csúcstól ugyanannyi:
r=|r-x0|=|r-x1|=|r-x2|=3.49585
és a r-bfxi vektorok lineárisan összefüggők, azaz a pont a háromszög síkjában van, tehát ez valóban a háromszög középpontja.
|
| Előzmény: [863] jonas, 2007-10-02 15:37:50 |
|
| [863] jonas | 2007-10-02 15:37:50 |
 Igen, noha fejből nem tudtam megmondani. Súlyozni kell a csúcsokat a csúcsban lévő szög kétszeresének a színuszával, és normálni ezeknek az összegével.
|
| Előzmény: [861] farkasb, 2007-10-02 00:06:56 |
|
| [862] Lóczi Lajos | 2007-10-02 13:29:35 |
 Minden attól függ, hogy milyen matematikai szövegkörnyezetben vagyunk. Pl. a háromszög is tekinthető körnek (és viszont), ha topológiai szemmel nézzük a dolgokat, ahol is csak a folytonos egymásba deformálhatóság számít.
|
| Előzmény: [860] Pokolfajzat, 2007-10-01 20:21:37 |
|
| [861] farkasb | 2007-10-02 00:06:56 |
 Tisztelt Fórumozók!
Érdeklődnék, hogy valaki tud-e képletet egy egy térbeli háromszög köré írható kör középpontjának kiszámítására, és a térbeli kör egyenletének felállítására. Előre is köszönettel: F.Balázs
|
|
| [860] Pokolfajzat | 2007-10-01 20:21:37 |
 Nincs különösebb jelentősége, csak részemről volt ez egy feltevés, másoknak. Akik azt mondták erre, hogy ez nem igaz, csakhogy az igazamat én sem tudtam ésszerűen alátámasztani. És reméltem, ha a feltevésem igaz akkor itt talán tudnak rá egyesek magyarázatot is adni.
|
|
|
| [858] Pokolfajzat | 2007-09-22 19:44:13 |
 Csak egy kérdéssel zavarnám meg a tisztes társaságot. Előre is elnézést kérek, ha banális vagy ostoba lenne a kérdés. Tekinthető e a kör egy végtelen sokszögnek? Előre is köszönöm.
|
|
|
| [856] SmallPotato | 2007-09-20 08:39:23 |
 Felhozom kicsit a topikot.
A 123. feladat megoldása:
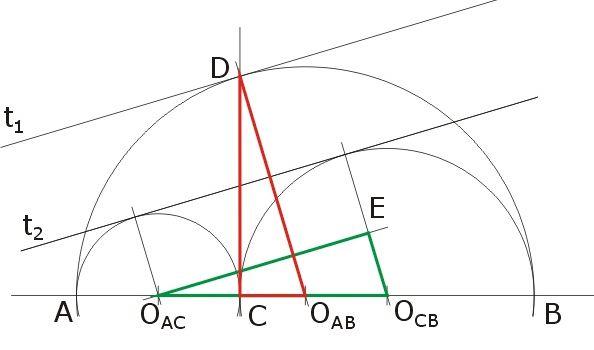
Kicsinyítsük az AB átmérőjű kört A-ból 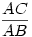 arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos. arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos.
A 120-as feladat megoldásából azonban ismert, hogy a rajzolt elrendezésben az AB kör D-beli érintője párhuzamos az AC és a CB körök közös külső érintőjével. Eszerint AC kör imént előállt (E pontbeli) érintője ezzel a közös érintővel egybeesik.
(Természetesen elindulhattunk volna az AB kört C-ből 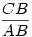 arányben kicsinyítve is.) arányben kicsinyítve is.)
|
| Előzmény: [854] BohnerGéza, 2007-09-05 23:57:21 |
|
|
|
| [853] sakkmath | 2007-08-30 09:20:48 |
 Köszönöm, hogy foglalkoztál a feladattal és feltetted a megoldásodat, ami természetesen helyes.
A feladat egyébként - elemi módon - még (legalább) két másik módszerrel is megoldható. Tehát nincs még lelőve semmi, aki esetleg új megoldásra bukkan, nyugodtan tegye fel...
|
| Előzmény: [851] SmallPotato, 2007-08-29 23:34:51 |
|
|
| [851] SmallPotato | 2007-08-29 23:34:51 |
 A 808-asra hoznék egy megoldást; úgy látom, eddig még nem érkezett.
Legyen 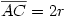 , és , és 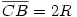 . .
Húzzunk párhuzamost t2-vel az OAC ponton át; messe ez a BC átmérőjű körnek a t2-vel való érintési pontjába húzott sugarát az E pontban. Ekkor 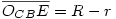 és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r. és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r.
Az OABDC háromszög C szöge derékszögű, 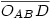 átfogója (lévén az átfogója (lévén az 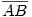 átmérőjű kör sugara) szintén R+r, és átmérőjű kör sugara) szintén R+r, és 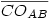 befogója szintén R-r, tehát befogója szintén R-r, tehát
az OACOCBE és a OABDC háromszögek egybevágók.
Eszerint viszont COABD =OACOCBE =OACOCBE , azaz , azaz 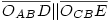 , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2. , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2.
|
 |
| Előzmény: [808] sakkmath, 2007-07-16 18:26:43 |
|
| [850] zizibi | 2007-08-24 18:31:31 |
 Köszönöm, segítséget. Így már értem.
Az az igazság ogy a 10. volt már majd 10 éve volt, de nem is azzal van a gond csak nem esett le az egyenlő együtthatók módszer.
Mégegyszer köszönöm! :)
|
| Előzmény: [849] BohnerGéza, 2007-08-24 16:29:24 |
|
| [849] BohnerGéza | 2007-08-24 16:29:24 |
 A számolásnál az egyenlő együttgatók módszerét használtam. Ha elvégezted volna a jelzett számolást, észrevetted volna, hogy y kiesik.
Próbáld ki! Az első egyenletet v2-vel, a másodikat v1-gyel szorozva, a kettőben x ua-szor lesz. Kivonva egymásból a kapott egyenleteket x kiesik, y kiszámolható.
Természetesen behelyettesítéssel is kijön ue.
Ezeket legalább tizedikes ismerőseidtől is megtudhattad volna.
|
| Előzmény: [848] zizibi, 2007-08-24 09:41:49 |
|
| [848] zizibi | 2007-08-24 09:41:49 |
 Hát igen, én bonyolultabban akartam megoldani :)
De azt nem igazán értem, hogy ha megszorzom az egyik egyenletet v1 a másikat v2-vel, akkor hova tűnik az y? Mert hát ha jól emlékszem, hiányos matektudásomban az van, hogy minden tagot szorozni kell, vagy nem? Ez valamiféle egyszerűsítés?
Elnézést, hogy ennyit értetlenkedem, de szeretném megérteni hátha jobban felfogom...
|
| Előzmény: [846] BohnerGéza, 2007-08-23 14:09:27 |
|
|
|
| [845] zizibi | 2007-08-23 11:33:56 |
 Igen, erre az egyenletre rá jöttem én is, de kéne még egy egyenlet, gondolom, amiből ki lehet fejezni az x-t és egy másik amiből az y-t.
Na idáig nem jutottam el. Vagy az egyik koordinát egyenletét be lehetne helyettesíteni a másikba, pl. x-et kifejezve belőle?
|
| Előzmény: [842] BohnerGéza, 2007-08-22 20:45:22 |
|
|
|
|
| [841] zizibi | 2007-08-22 14:26:32 |
 Kedves BohnerGéza!
Még egyszer köszönöm az előző segítséget, remekül tudom használni (bár koordinátarsz-re nem volt szükségem, mert karakteresen működik a program), de nem igazán értem, hogy Pithagórasz-tétel hogyan is működik ebben az esetben.
Közben pedig újabb problémába ütköztem.
Szintén koordináta jellegü és az előző feladat megfordítása, vagyis adott AB egyenes és egy X pont. Meg szeretném tudni, hogy az X pont milyen merőleges távolságra van A-tól, AB egyenesen mérve illetve milyen messze van AB egyenestől.
Szögfügvényekkel találtam megoldást, de nekem jobban tetszene egy, az előzőhöz hasonló megoldás.
Előre is köszönöm a segítséget!
|
| Előzmény: [836] BohnerGéza, 2007-08-16 21:56:13 |
|




 -
- 0)=(v1,v2)/(|v1|.|v2|)=0.0118753
0)=(v1,v2)/(|v1|.|v2|)=0.0118753


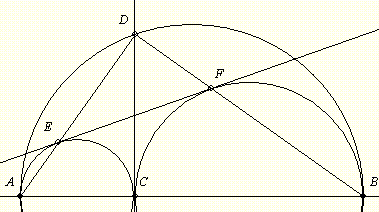

 =OACOCBE
=OACOCBE