Fórum: Csak logika

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30]

Szeretnél hozzászólni? Jelentkezz be.

[440] Róbert Gida

2012-12-05 21:47:29

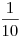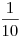$\frac {1}{10}$ a válasz, feltételes valószínűséggel kijön. De el is lehet "mesélni": 18 húzásból 9-szer otthon van a kulcs, míg a többi 1-1 esetben a fiókok egyikében. Ezek közül 8 eset kiment, hiszen 8 fiókban nincs kulcs, maradt 10 eset, ezek közül csak egyben van a kulcs a munkahelyen, így $\frac {1}{10}$ a valószínűség.

Kicsit http://en.wikipedia.org/wiki/Monty_Hall_problem típusú a probléma azt is nézve, hogy sok válasz adható rá.

Előzmény: [429] Hajba Károly, 2012-12-03 00:40:17

[439] polarka	2012-12-05 19:28:50
100%-osan?
Előzmény: [438] polarka, 2012-12-05 19:27:19

[438] polarka	2012-12-05 19:27:19
És a kolléga állításában/nyilatkozatában/kijelentésében megbízunk 100
Előzmény: [432] Hajba Károly, 2012-12-03 20:18:27

[437] jonas	2012-12-05 19:09:41
Szerintem a bolygók száma tetszőleges páros szám lehet.
Előzmény: [434] w, 2012-12-05 16:00:34

[436] Hajba Károly

2012-12-05 18:29:26

Azért ez nem ennyire egyszerű. Így fel sem tettem volna.

:o)

Előzmény: [433] w, 2012-12-03 21:44:43

[435] w

2012-12-05 17:38:58

Egy dobozban 2012 fehér golyónk van és még feleslegben piros és zöld golyó a dobozon kívül. Cserélgetjük a golyókat, ezt a következő módon tehetjük:

(1.) két zöldet két fehérre és fordítva,

(2.) három pirosat és egy fehéret egy zöldre,

(3.) egy zöldet és két fehéret két pirosra,

(4.) öt zöldet két pirosra és két fehérre, vagy végül

(5.) egy pirosat és egy zöldet egy fehérre cserélünk.

A feladat:

a) Tegyük fel, hogy valahány csere után három golyó marad a dobozban. Mutassuk meg, hogy ezek háromféle színűek!

b) Elérhető-e, hogy három golyó maradjon?

[434] w	2012-12-05 16:00:34
Adott n darab bolygó, ezek mindegyikén egy-egy csillagász (képzeletbeli, zárt rendszerről van szó). Mindegyik csillagász figyeli a hozzá legközelebb eső valamelyik bolygót (de nem azt, amelyiken van). Tudjuk, hogy minden bolygót valamelyik csillagász megfigyelés alatt tartja. Mennyi lehet n értéke, ha nincs két azonos bolygóközötti távolság?

[433] w

2012-12-03 21:44:43

Az ilyen típusú példák általában beugratósak és igen nehezek, de azért hátha ez nem :)

Vagy otthon, vagy a munkahelyen van; ha a munkahelyen, akkor biztos a megmaradó fiókban, ez ad 1/2 valószínűséget.

Előzmény: [432] Hajba Károly, 2012-12-03 20:18:27

[432] Hajba Károly	2012-12-03 20:18:27
A kolléga 3-ról nyilatkozott. Én a maradék 6-ből 5-öt néztem meg. 1 maradt megnézetlen.
Előzmény: [431] Hajba Károly, 2012-12-03 20:16:29

[431] Hajba Károly	2012-12-03 20:16:29
A kolléga 3-ról nyilatkozott.
Előzmény: [430] jonas, 2012-12-03 18:00:53

[430] jonas	2012-12-03 18:00:53
Tehát te a megmaradó hat fiókból néztél meg ötöt, miután a kollégád már megmondta, melyik öt fiók kizárt?
Előzmény: [429] Hajba Károly, 2012-12-03 00:40:17

[429] Hajba Károly	2012-12-03 00:40:17
Keresem a kulcsom. Fele-fele valószínűséggel a munkahelyemen vagy otthon lehetséges. A munkahelyemen 9 fiók van, melyekben lehetséges. Ebből 3-ról a kollégám kijelentette, hogy ott nincs. Én 5-t megnéztem és nem volt ott. Milyen valószínűséggel van a 9. fiókban a kulcs?

[428] Moderátor

2012-04-03 12:54:27

Bily, ez a téma a teljesen elemi, számolás nélküli logikai feladatok megbeszéléséért van.

Hagyd abba az offolást.

[427] bily71	2012-04-03 07:12:06
Javítás: $2^k \cdot\binom{n}k$ darab egyenletünk van, ahol 2^k konstans.
Előzmény: [425] bily71, 2012-04-02 21:03:36

[426] bily71	2012-04-02 21:30:44
Tegyük fel, hogy nem jól gondolom és n>3 esetben látszik az origóból egy csúcs és L mégiscsak korlátos, ebben az esetben az segíthet, hogy ekkor a 2n darab x_j=z min/max értékek között biztosan létezik olyan, hogy \|z\|>1, márpedig ez is kideríthető polinom időben a polinom sok LP-ről.
Előzmény: [425] bily71, 2012-04-02 21:03:36

[425] bily71

2012-04-02 21:03:36

Nem, nem, szó sincs itt 16 egyenletről.

Félreérthetően fogalmaztam, igazából nem n-dimenziós oktaéderről van szó, hanem valami hasonlóról.

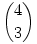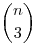Az n=4,k=3 esetben $\binom43$ egyenletet kapunk, általában $\binom {n}3$ egyenletet, de most maradjunk az n=4 esetnél.

A 32 egyenlet 32 síkot határoz meg, az L pontjai a síkoktól az origó felé eső térrészek metszetének pontjai ugyanúgy, mint az n=3 esetben, ezek a síkok 4 db 3D-s oktaédert, összesen egy ezekből álló 4D-s konvex, korlátos poliédert határoznak meg.

A 4D-s kocka egy csúcsa most is akkor látszik az origóból, ha nem takarják síkok. Egy csúcsot összesen 4 darab sík takarhat, ha ezeket elhagyjuk a feltételrendszerből, akkor L konvex, nem korlátos poliéder, ekkor legalább egy LP-nek nincs optimális megoldása, ha csak 3-at hagyunk el, vagy nem egyazon csúcsot takaró 4-et, akkor L konvex, korlátos poliéder, ekkor mindegyik LP-nek van optimális megoldása.

Lássunk néhány konkrét példát, ahol csak A-t írjuk fel:

$\matrix{ 0&1&1&-1\cr 0&1&-1&1\cr 0&1&-1&-1\cr 0&-1&1&1\cr 0&-1&1&-1\cr 0&-1&-1&1\cr 0&-1&-1&-1\cr 1&0&1&-1\cr 1&0&-1&1\cr 1&0&-1&-1\cr -1&0&1&1\cr -1&0&1&-1\cr -1&0&-1&1\cr -1&0&-1&-1\cr 1&1&0&-1\cr 1&-1&0&1\cr 1&-1&0&-1\cr -1&1&0&1\cr -1&1&0&-1\cr -1&-1&0&1\cr -1&-1&0&-1\cr 1&1&-1&0\cr 1&-1&1&0\cr 1&-1&-1&0\cr -1&1&1&0\cr -1&1&-1&0\cr -1&-1&1&0\cr -1&-1&-1&0\cr }$

Itt 4 síkot hagytunk ki:

x₁+x₂+x₃ $\ge$ -1

x₁+x₂+x₄ $\ge$ -1

x₁+x₃+x₄ $\ge$ -1

x₂+x₃+x₄ $\ge$ -1

Ezek az (-1,-1,-1,-1) csúcsot takarták, ami most már látható az orgóból, hiszen ebben az irányban mind a 4 odarab 3D-s oktaéder , így az azokból álló 4D-s valami is nyitott, ezért L nem korlátos és ez a csúcs/vektor/klóz része L-nek és kielégíti F₃⁴-et, stb.

$\matrix{ 0&1&1&-1\cr 0&1&-1&1\cr 0&1&-1&-1\cr 0&-1&1&1\cr 0&-1&1&-1\cr 0&-1&-1&1\cr 0&-1&-1&-1\cr 1&0&1&-1\cr 1&0&-1&1\cr 1&0&-1&-1\cr -1&0&1&1\cr -1&0&1&-1\cr -1&0&-1&1\cr -1&0&-1&-1\cr 1&1&0&-1\cr 1&-1&0&1\cr 1&-1&0&-1\cr -1&1&0&1\cr -1&1&0&-1\cr -1&-1&0&1\cr -1&-1&0&-1\cr 1&1&1&0\cr 1&1&-1&0\cr 1&-1&1&0\cr 1&-1&-1&0\cr -1&1&-1&0\cr -1&-1&1&0\cr -1&-1&-1&0\cr }$

Itt is négyet hagytunk ki:

-x₁+x₂+x₃ $\ge$ -1

x₁+x₂+x₄ $\ge$ -1

x₁+x₃+x₄ $\ge$ -1

x₂+x₃+x₄ $\ge$ -1

de ezek klünböző csúcsokat takarnak, ezért L korlátos, így nem látható az origóból és ezért nem is esik bele egyik csúcs sem, továbbá minden LP megoldható és F₃⁴ nem kielégíthető.

Ha a kihagyott egyenletek között van legalább egy olyan négyes, mely egyazon csúcsot takart, akkor F₃⁴ kielégíthető, ekkor L nem, korlátos, így nincs minden LP-nek optimális megoldása.

Remélem így már érthetőbb, azt meg nem tudom képlettel leírni, hogy egy sík takarja a csúcsot az origóból, ezért írtam szemléletesen.

Előzmény: [424] Kemény Legény, 2012-04-02 15:29:38

[424] Kemény Legény	2012-04-02 15:29:38
Hogy kicsit konkrétabb legyek: kérlek, írd fel azt a 16 egyenletet ami az n=4 dimenziós oktaédered lapjait írják le. Majd hasonlítsd ezt össze azzal a 32 egyenlettel, amelyek a k=3 feltétel alapján kijönnek. Mintha olyasmit állítanál, hogy az utóbbi 32 egyenlet részhalmazát alkotja a 16 másiknak...Vagy ha mégsem ezt állítod, akkor kérlek, formalizáld meg pontosan, mit állítasz.
Előzmény: [423] Kemény Legény, 2012-04-02 15:03:37

[423] Kemény Legény

2012-04-02 15:03:37

Az n=3, k=3 esetről készséggel elhiszem, hogy polinom időben megoldod :)

Kicsit részletesebben is kifejthetnéd az általános esetet, képletekkel(!), nem pedig szemléletesen. Úgy vélem, épp ez lenne a lényege a "bizonyításodnak", mégis 1 mondattal átsiklasz felette...

Előzmény: [422] bily71, 2012-04-02 14:16:16

[422] bily71

2012-04-02 14:16:16

Hogy ne egészértékű programozási feladatról legyen szó, módosítsuk egy kicsit a feltételrendszert.

Tekintsük a következő 2n darab LP feladatot, ahol a_ij $\in$ A= $\varphi$ (F₃ⁿ), x₁,x₂,...,x_n $\in$ R:

a₁₁x₁+a₁₂x₂+...+a_1nx_n $\ge$ -1

a₂₁x₁+a₂₂x₂+...+a_2nx_n $\ge$ -1

...

a_m1x₁+a_m2x₂+...+a_mnx_n $\ge$ -1

---------------------------------

x_j=z $\to$ min /max

Állítás: F₃ⁿ pontosan akkor kielégíthető, ha a 2n darab LP feladat közül legalább egynek nincs optimális megoldása.

Bizonyítás: Tekintsük az n=3 esetet, ekkor az A mátrix sorai olyan síkok egyenletei, melyek egy olyan oktaéder határoló síkjai, melynek csúcsai a 2 élhosszúságú, origó középpotú kocka lapközéppontjai.

Bármik is legyenek az a_ij értékek, az origó mindig eleme a megoldáshalmaznak (L) , erről meggyőződhetünk, ha az x₁,x₂,...,x_n helyére 0-t írunk.

F₃³ pontosan akkor kielégíthető, ha a kocka legalább egy csúcsa L-ben van. A kocka egy csúcsa akkor lehet eleme L-nek, ha "látszik" az origóból, vagyis, ha a feltételrendszerból hiányzik az oktaéder egyik határoló síkja, mely "eltakarja" a csúcsot. Valóban, L azon pontok halmaza, melyek az A sorai által leírt síkoktól az origó felé eső térrészek metszetében vannak, így, ha van a kocka csúcsát és az origót elválasztó ilyen sík, akkor a kocka csúcsa nem lehet eleme L-nek, hiszen a síktól nem az origó felé eső térrészben van.

Ha elhagyunk legalább egyet az oktaédert határoló síkokból, akkor a megmaradt síkok által határolt L egy konvex, nem korlátos poliéder lesz (triviális).

Mindezekből következik, hogy ha F₃³ kielégíthető, vagyis ha a kocka legalább egy csúcsa eleme L-nek, akkor L nem lehet korlátos. Ha L nem korlátos, akkor a 2n darab LP feladat közül legalább egynek nincs optimális megoldása (triviális). Ha L korlátos, akkor minden csúcs L-en kívül esik, ekkor F₃³ nem kielégíthető és minden LP-nek van optimális megoldása.

n>3 esetben (n=1,n=2 esetén is) az előbbiekhez hasonlóan járunk el, ott az n-dimenziós "kockát" és a kockába írt "oktaédert" használjuk a bizonyítás során. Az állítást igazoltuk minden n-re.

Az előbbi 2n darab LP feladatról polinom időben megállapítható, hogy köztük legalább egynek nincs optimális megoldása, vagy mind megoldható, ezért a 3-SAT problémára polinom időben választ kapunk, ebből már következik [419] végkövetkeztetése.

Előzmény: [420] Róbert Gida, 2012-03-31 22:49:27

[421] bily71

2012-04-01 13:26:23

Kellemesen csalódtam, elolvastad, mielőtt hozzászóltál. :)

Az LP feleadat úgy lett megkonstruálva, hogy ha van valós értékű megoldás, akkor van egészértékű is, pontosabban: a hiperkocka és a megoldáshalmaz metszete vagy üres, vagy tartalmazza a hiperkocka egyik csúcsát, így az x_j $\in$ {-1,1} kikötés felesleges.

Ez persze bizonyításra szorul, k=3 esetben ez sikerült is, később leírom.

Előzmény: [420] Róbert Gida, 2012-03-31 22:49:27

[420] Róbert Gida

2012-03-31 22:49:27

Ha egészértékű megoldást keresel, akkor bizony egészértékű programozási feladatról van szó és nem LP-ről. Így pedig a feladatod NP nehéz.

Gyanús is lenne egy fél oldalas bizonyítás arra, hogy P=NP.

Előzmény: [419] bily71, 2012-03-31 14:07:33

[419] bily71

2012-03-31 14:07:33

Feladat: (k-SAT probléma) Kielégíthető-e az F_kⁿ= $\Lambda$ _i=1^mC_i= $\Lambda$ _i=1^mV_j=1ⁿP_ij n változós konjunktív normálforma, ahol minden klóz pontosan k nem üres literált tartalmaz?

Megoldás: (i) F_kⁿ kielégíthető, ha létezik C n változós klóz, melyben minden literál nem üres, úgy, hogy bármely C_i klóztól legfeljebb k-1 nem üres literálban tér el. Az előbbi állítás következik a kielégíthetőség definíciójából.

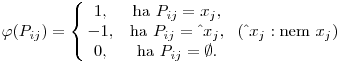
Legyen V vektortér a T=GF(3) test felett és $\varphi$ :F_kⁿ $\to$ A $\in$ T^m×n,P_ij $\mapsto$ a_ij, ahol $\varphi(P_{ij})=\left\{\matrix{1,&{\rm{ha}}~P_{ij}=x_j, \cr -1,&{\rm{ha}}~P_{ij}=\^ ~x_j ,\cr 0,&{\rm{ha}}~P_{ij}=\emptyset .}\right.~(\^ ~x_j: {\rm{nem}}~x_j)$

Az A mátrix sorvektorai lesznek a klózok képei: $\varphi$ (C_i)=c_i $\in$ V.

Az (i) állítás így hangzik a vektorok nyelvén: F_kⁿ kielégíthető, ha létezik x $\in$ V, (x^T=(x₁,x₂,...,x_n), ahol x_i $\in$ {-1,1}) úgy, hogy bármely c_i-től legfeljebb k-1 nem 0 koordinátában tér el, vagyis <x,c_i> $\ge$ 2-k, ahol <x,c_i> a skaláris szorzat.

Az előbbi egyenlőtlenség A minden sorára igaz, így egy egyenletlőtlenség rendszert kapunk: A x $\ge$ b, b^T=(2-k,2-k,...,2-k), vagyis

a₁₁x₁+a₁₂x₂+...+a_1nx_n $\ge$ 2-k

a₂₁x₁+a₂₂x₂+...+a_2nx_n $\ge$ 2-k

...

a_m1x₁+a_m2x₂+...+a_mnx_n $\ge$ 2-k

Koordináta rendszerbenben ábrázolva az x vektor egy n dimenziós, 2 élhosszúságú, origó középpontú hiperkocka egy csúcsába mutató helyvektor, így egyúttal a hiperkockát határoló egyik hipersík egy pontjába mutató helyvektor is. Ilyen határoló x_j= $\pm$ 1 egyenletű hipersíkból pontosan 2n darab van, ezek közül eggyel kiegészítve az egyenlőtlenség rendszert 2n darab

a₁₁x₁+a₁₂x₂+...+a_1nx_n $\ge$ 2-k

a₂₁x₁+a₂₂x₂+...+a_2nx_n $\ge$ 2-k

...

a_m1x₁+a_m2x₂+...+a_mnx_n $\ge$ 2-k

x_j= $\pm$ 1

alakú egyenlőtlenség rendszert kapunk, melyek közül (a konstrukció miatt) ha egy is megoldható, akkor F_n^k kielégíthető, ha egyiknek sincs megoldása, akkor nem kielégíthető.

Alakítsuk át a kapott 2n darab egyenlőtlenség rendszert 2n darab lineáris programozási (LP) feladattá, ehhez szükségünk lesz feladatonként egy-egy célfüggvényre. Legyen ez praktikusan x_j=z $\to$ max . Most már van 2n (polinomiális sok) darab

a₁₁x₁+a₁₂x₂+...+a_1nx_n $\ge$ 2-k

a₂₁x₁+a₂₂x₂+...+a_2nx_n $\ge$ 2-k

...

a_m1x₁+a_m2x₂+...+a_mnx_n $\ge$ 2-k

x_j= $\pm$ 1

----------------------------------

x_j=z $\to$ max

alakú LP feladatunk, melyek mindegyike megoldható (például a Karmarkar algoritmus segítségével) polinomiális idő alatt.

Következmény: Találtunk egy algoritmust, mely polinomiális időben választ a k-SAT problémára, mely NP-ben van, ezért

P=NP

[418] lorantfy	2011-06-14 11:06:57
Három vándor találkozik, mindegyiküknél van valamennyi pénz. Az egyik ad a másik kettő mindegyikének negyedannyi pénzt, mint amennyi épp nála van. Ezután ugyanezt teszi a másik, majd a harmadik vándor. Végül mindegyiküknél 16-16-16 tallér lesz. Hány tallér volt a találkozáskor a leggazdagabb vándornál?

[417] physis

2011-02-03 08:29:32

Szerintem az lehet a legérdekesebb kérdés, hogy egyáltalán milyen úton is jön rá a megoldásra az ember. Szerintem ez az út szinte minden embernél más és más. Sokszor furcsa és kacskaringós is lehet, amit többnyire a végső megoldás felírásakor el is titkolnak, mint ahogy Gauß tette állítólag (ha kész az épület, az állványt lebontjuk, meg: róka, aki eltörli az ösvényt a saját nyomában, stb). Gondolom, a heurisztika többnyire privát marad, vagy legalábbis intim, de még ha nem is, akkor is inkább csak élőszóban él, akárcsak a bajor dialektusok, és az intim élőnyelvinél szervezettebb közrebocsátásuk furcsán hatna, akárcsak egy konyhanyelv hivatalos nyelvként való használásával poénkodó hivatalos közlemény (ez egyébként egy hivatalos német társadalmi hirdetés paródiája, az eredeti ez lenne).

Én úgy jöttem rá a pénzérmés példa megfejtésére, hogy:

Előszőr a feladatot csak piciben próbáltam elképzelni: ,,Négy érme az asztalon, tudjuk, hogy közülük kettő a fej. Osszuk az érméket kétfelé úgy, hogy a két-két csoportban a fejek száma egyenlő legyen.''

E a minipélda elég kicsi ahhoz, hogy az ember könnyen ellenőrizze sejtéseit (ötlet híján akár a véges esetek kézi kimerítésével is), így aztán könnyen lehet hipotéziseket felállítani és tesztelni, először akár a legvadabb ötletek között is válogatva.

Hamar kiderül, hogy egyfajta ,,round robin'' algoritmus beválik: felváltva húzzuk az érméket az egyik, ill. másik csoportba, és minden másodikon (vagyis épp ,,a másik'' csoportba kerülőkön) egyúttal fordítunk is egyet. Persze lehet még sok más stratégia, de ez a ,,round robin'' az egyik legegyszerűbb, és ezért én az elsők között próbálkoztam vele.

Persze a ,,round robin'' csak igen speciális (vagyis fele-fele) fej-írás kezdeti arány esetén ad jó eredményt! Persze ez nem is csoda, hiszen a ,,round robin'' a legesleglő próbálkozásom volt, amit eleve direkt a speciálisan a szimmetrikus minipéldára fejlesztettem ki. Éppen ezért is ilyen ,,szimmetrikus'' a ,,round robin'' működési előfeltétele.

Viszont ha a kezdeti fej és írás arány nem fele-fele lenne, sőt, ha esetleg eleve páratlan is az érmék száma, akkor persze a ,,round robin'' helyett más, szándékosan ,,aszimemtrikus'' stratégiát kéne bevetni. Erre is lehet minipéldát találni (,,három érme az asztalon, közülük két fej''), és e minipélda fölött szintén lehet akár favágó esetkimerítéssel is hipotéziseket tesztelni. Itt pl. az alábbi stratégia ugrott be nekem először: ,,balra-fordítással, jobbra-békénhagyva, balra-fordítással''.

Az egyelőre sokféle szóbajövő stratégia miatt, a következő lépésem az általánosítás volt, hiszen az eddigi stratégiák csak igen speciális fej-írás kezdeti arány esetén adnak jó eredményt. Viszont arra igenis jók voltak ezek a minipéldák, ministratégiák, hogy az ő révükön felismerjek néhány törvényt, afféle ,,minitételt''. Persze a törvények általános megfogalmazásához túl kellett lépnem a konkrét példákon, és valami egységes sémát kellett kitalálnom az összes lehetséges ,,stratégia'' egységes specifikálására.

Épp erre találtam ki a ,,maszk'', ,,rács'' fogalmát: a fényképészek, grafikusok által használatos mindenféle kitakaró és stencilező árnyékoló és szűrő fóliák analógiájára. Minden lehetséges stratégiát meghatároz egy fólia, a ,,round robin'' ezek közül az, ahol a fólia ,,lyukai'' és fogai épp a lyuk-fog-lyuk-fog minta szerint állnak. A másik említett ,,aszimmetrikus'' stratégia pedig pedig az, amelyet épp a fog-lyuk-fog maszkminta specifikálna.

Később persze kiderült, hogy a ,,maszk'' fogalma redundáns, pazarló (hiszen a maszk elrendezése úgysem számít, csak a fogak és a lyukak egymáshoz mért aránya), de engem mégis ez a fogalom segített hozzá ahhoz, hogy rájöjjek a megoldásra.

A lehetséges maszkok és feladatok kombinációit paraméterezve, hamar kijött egy alapegyenlet, amiből már el lehetett jutni a megoldáshoz. n érme, közülük k fej esetén a ,,maszkot'' úgy kell megválasztani, hogy r lyuka legyen, ahol

n=r+k

vagyis - talán szemléletesebben

r=n-k

vagyis a lyukak száma épp az írások kezdeti számával egyezzék meg. A rács pontos alakja nem lényeges, csak a lyukszáma (épp ezért erősen redundáns fogalom is, de ideiglenes heurisztikaiként nekem nagyon jó volt.)

Amikor meg már ez megvolt, a megoldást már le lehetett írni az állványzat és a heurisztikus segédfogalmak nélkül is. Én azért heurisztikai okokból mégis meghagytam (appendixben) a maszkok és a ,,round robin'' leírását, legalább említésképp.

A részleteket, a teljes bejárt heurisztikai út leírását ide tettem fel.

Előzmény: [380] lorantfy, 2010-11-14 21:43:16

[416] sakkmath

2011-02-01 14:12:54

Feltesszük, hogy Csirmaz Áprilisi fejtörőjét megoldottuk.

A kapott számértékek felhasználásával [412] így részletezhető:

A majom életkora, azaz: "majomi age": 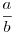$\frac{a}{b}$ , ami egy valódi tört; ebből a "szorzatos kapcsolat": ab. Utóbbit visszafelé olvasva - erre utal az ega - megkapjuk egy olyan személy életkorát (egész években), akinek május 27-én (05.27.) van a szülinapja :)

Az Áprilisi fejtörő ismeretlenei közül háromnak azonos a számértéke, s ennek közönséges tört alakjában szerepel a 22 (innen a 3-szoros öröm). A negyedik öröm a 27-5=22-ből adódik.

A 22-vel kapcsolatos a "hetenként", de ezt nem lövöm le, hátha lesz valaki, aki csak ez után oldja meg a Csirmaz-feladatot :)

(Ha túlbonyolítottam, elnézést - talán most érthetőbb.)

Bónusz kérdés: Mit csinált Python? :))

Előzmény: [415] Csimby, 2011-01-31 23:55:09

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30]

Már regisztráltál?
Új vendég vagy?