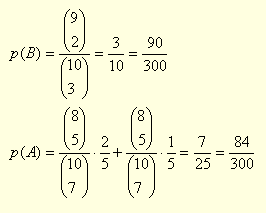| [695] Maga Péter | 2013-01-26 18:33:06 |
 Akár egymástól függetlenül sorsolják a sapkákat, akár nem, az elképzelt stratégiában a rabok nyilván nem egymástól függetlenül* tippelnek. Emberünk persze -- mint mindenki más -- 1/2 eséllyel elbukik, de ezek az elbukások nem független események.
* 'nem egymástól függetlenül': a valószínűségi értelemben értendő; a szabályoknak megfelelően persze nem használják egymás tippjeit, tehát ebben persze egymástól függetlenül, de nem erről beszélek
-----
A nagy félrecsúszás elkerülése céljából: ez egy logika (vagy tetszés szerint halmazelmélet) feladat, nem valószínűségszámítás. Kicsit sok volt a Monty Hall, ennek a feladatnak semmi köze a valószínűségekhez. Nyilván egy valószínűségi módszert használó rossz megoldás valószínűségi hibát vét, csak azért valószínűségeztem, hogy ezt elmagyarázzam.
|
| Előzmény: [691] Micimackó, 2013-01-26 17:41:29 |
|
|
| [693] Maga Péter | 2013-01-26 18:14:51 |
 Ha véges számú rabról van szó, akkor minden stratégiára igaz, hogy tetszőleges sapkakiosztás után véges sokan veszítenek. A konkrét stratégiát is le lehet hozni véges sok ember esetére (bár elég semmitmondó lesz).
|
| Előzmény: [692] HoA, 2013-01-26 17:46:07 |
|
|
| [691] Micimackó | 2013-01-26 17:41:29 |
 Szerintem ez mindenképpen igaz, ha feltesszük, hogy a sapkákat egymástól függetlenül sorsolják (amit feltehetünk): Ekkor emberünk a többiek fején lát valamit, ez alapján tippel valamit (mondjuk kéket), de 0.5 eséllyel piros van a fején.
|
| Előzmény: [690] Maga Péter, 2013-01-26 15:08:19 |
|
| [690] Maga Péter | 2013-01-26 15:08:19 |
 ,,(...) minden ember 0.5 eséllyel téveszti el a sapkája színét.''
Ha véletlenszerűen tippel, akkor ez igaz. Segítség: a többiek sapkáját látva mindenki le tud szűrni egy elég természetellenes információt. Mi lehet az?
|
| Előzmény: [689] Micimackó, 2013-01-26 12:45:48 |
|
| [689] Micimackó | 2013-01-26 12:45:48 |
 Úgy sejtem nem lehet, hiszen minden ember 0.5 eséllyel téveszti el a sapkája színét. Annak az esélye, hogy "végtelen sok 0.5-os esemény közül csak véges sok esemény következik be" maximum 0.5 lehet.
|
| Előzmény: [682] Maga Péter, 2013-01-19 12:52:56 |
|
| [688] Micimackó | 2013-01-26 12:22:49 |
 "Itt értem a "stratégia" jelentését, hiszen mindenki a már elhangzott tippek és az előtte látható sapkák alapján alakíthatja tippjét." - A stratégia itt is ugyanazt jelenti, de itt a tipp, csak a többiek sapkájától függhet: az emberek meg vannak számozva, és tudod hányas számúnak milyen színű a sapkája, kivéve a sajátod.
|
| Előzmény: [686] HoA, 2013-01-25 20:58:56 |
|
| [687] Maga Péter | 2013-01-25 22:27:22 |
 A következőt értjük stratégia alatt. A piros és kék sapkát röviden rendre 0-val, illetve 1-gyel jelölöm.
Legyen az emberek halmaza I, egy adott sapkakiosztás pedig egy f:I {0,1} függvény, legyen F ezen függvények halmaza. Adott x {0,1} függvény, legyen F ezen függvények halmaza. Adott x I-re az x ember I-re az x ember  x stratégiája egy x stratégiája egy  x:F x:F {0,1} függvény, melyre teljesül, hogy ha f és g csak az x-ben térnek el, akkor {0,1} függvény, melyre teljesül, hogy ha f és g csak az x-ben térnek el, akkor  x(f)= x(f)= x(g) ('saját magát nem látja'). x(g) ('saját magát nem látja').
Egy  stratégia ezek összessége, tehát egy függvény I×F-ről {0,1}-be, mely minden egyes x stratégia ezek összessége, tehát egy függvény I×F-ről {0,1}-be, mely minden egyes x I-re konstans az F-beli függvény x feletti megváltoztatása során, azaz I-re konstans az F-beli függvény x feletti megváltoztatása során, azaz  (x,f)= (x,f)= (x,g), ha minden x-től különböző y (x,g), ha minden x-től különböző y I-re f(y)=g(y). I-re f(y)=g(y).
A kérdés pedig az, hogy van-e olyan  , hogy , hogy  (x,f)=f(x), minden egyes f (x,f)=f(x), minden egyes f F-re legfeljebb véges sok x kivételével. F-re legfeljebb véges sok x kivételével.
|
| Előzmény: [686] HoA, 2013-01-25 20:58:56 |
|
| [686] HoA | 2013-01-25 20:58:56 |
 Azt ismerem, ahol n db ( végses számú ) rabot a fejükre húzott kék és piros sapkákkal egymás mögé sorba állítanak, tehát mindenki látja az összes előtte álló sapkáját, de nem látja a sajátját és a mögötte állókét. A leghátsó mond egy tippet a saját sapkája színére, amit mindenki hall, majd az előtte álló, és így tovább. Itt értem a "stratégia" jelentését, hiszen mindenki a már elhangzott tippek és az előtte látható sapkák alapján alakíthatja tippjét. De hogyan beszélhetünk stratégiáról, ha egyszerre kell tippelni? Persze lehet, hogy a végtelennel van a turpisság.
|
| Előzmény: [682] Maga Péter, 2013-01-19 12:52:56 |
|
| [685] Fálesz Mihály | 2013-01-21 20:36:46 |
 Egy másik, a Csaszi bácsi féle Analízis Tanszék régi stenciljeinek idejéből származó gyakorlat.
Tagadjuk a következő állítást:
| ,,Minden asszony életében jön (van) egy pillanat, mikor olyat akar tenni, amit nem szabad.'' (Hofi) |
|
(Írjuk fel kvantorokkal, tagadjuk, majd fogalmazzuk meg a tagadást szövegesen is. Végül zenésítsük meg.)
|
|
|
|
| [682] Maga Péter | 2013-01-19 12:52:56 |
 Új feladat. Aki már hallotta, de lője le!
Egy börtönben (mondjuk megszámlálhatóan) végtelen sok rabot őriznek. Egy alkalommal a következőt ajánlják fel nekik. Mindegyiküknek a fejére tesznek egy piros vagy kék sapkát, ezután a többiek sapkáját látva (de a sajátjukat nem) mindannyiuknak egyszerre tippelnie kell a saját sapkájának színére. Aki eltalálja, azt szabadon engedik, aki nem találja el, azt kivégzik.
A rabok megbeszélhetnek egy stratégiát. Ki tudnak-e találni egy olyan stratégiát, amelynek segítségével véges sok kivételtől eltekintve mind kiszabadulnak?
|
|
|
| [680] Ménkűnagy Bundáskutya | 2013-01-18 23:08:30 |
 Úgy számoltam, hogy rendre 6/90, 42/90, 42/90 valséggel van 2, 1, 0 kulcs az elsőként kiválasztott három dobozban. Onnan rendre 0, 1/5, 2/5 valséggel nyerünk, tehát összesen 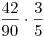 esélyünk van, ami annyi, amennyi. esélyünk van, ami annyi, amennyi.
Tényleg nem értettem teljesen, mit akarsz. Kicsit igen, azért emeltem ki a 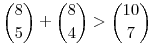 -t. -t.
|
| Előzmény: [679] Solaris, 2013-01-18 22:39:16 |
|
| [679] Solaris | 2013-01-18 22:39:16 |
 Hmmm, valóban nem írtam gondolatmenetet, hiszen lényegében egyszerű kombinatorika. Nem löktem a megoldást, hanem közöltem először az eredményt, majd amikor Alma megírta, hogy ő mást kapott p(B)-re, közöltem a képletet is. Te ugyan rámutattál, hogy valami nem stimmel, de nem találtad meg a képletben a hibát és nem is adtad meg, hogy te hogyan számoltál. Aki érti, az megmutatta volna, hogy mi nem helyes, mert képes kitalálni a másik gondolatmenetét. Talán a matematika tanár nem képes kijavítani a diákja hibás dolgozatát? Ugyan már! Légy szives ne nyilatkozz alaptalanul.
|
| Előzmény: [678] Ménkűnagy Bundáskutya, 2013-01-18 22:01:51 |
|
|
|
|
|
| [674] Alma | 2013-01-18 19:51:20 |
 Köszönöm a magyarázatot, de ezekkel tisztában vagyok, én is így számoltam. Arra mondj valamit, amit Ménkűnagy Bundáskutya mondott! Ha összeadod a te számolásodban, hogy hányféleképpen tudsz hét darab összesen pontosan egy, illetve pontosan két golyót tartalmazó dobozt kiválasztani, akkor nagyobb számot kapsz, mint ha azt számolod ki, hányféleképpen tudsz tíz dobozból hét akármilyet kiválasztani. Ez hibára utal a számolásodban.
|
| Előzmény: [672] Solaris, 2013-01-18 19:25:35 |
|
| [673] Solaris | 2013-01-18 19:32:23 |
 "A" jelentse azt az eseményt, hogy a maradék öt dobozban legalább egy golyó van. Utóbbi úgy valósulhat meg, ha a dobozokban pontosan két golyó van, illetve úgy is, hogy a dobozokban pontosan egy golyó van."
Ez így nem jó!
Helyesen: "C" jelentse azt az esemény, hogy ....
A lemaradt folytatás:
Az öt dobozból kiválasztunk egyet. "A" jelentse azt az eseményt, hogy a kiválasztott dobozban golyó van.
Elnézést!
|
| Előzmény: [672] Solaris, 2013-01-18 19:25:35 |
|
| [672] Solaris | 2013-01-18 19:25:35 |
 Az ilyen és ehhez hasonló feladatokat úgy a legcélszerűbb megoldani, hogy miután megértettük miről is van szó, lefosztjuk róla a meseszerű show elemeket és modellt készítünk. A számításainkat a modellen végezzük.
Vegyük szemügyre a B esetet. Itt egyszerűen arról van szó, hogy 10 egyforma doboz egyikébe elhelyezünk egy golyót. A dobozokat jól összekeverjük, majd kiválasztunk hármat. "B" jelentse azt az eseményt, hogy a kiválasztott három doboz egyikében ott a golyó.
Az A eset nem ennyire egyszerű. 10 egyforma dobozból kettőbe egy - egy golyót teszünk. A dobozokat összekeverjük, majd kiválasztunk hármat, amit a továbbiakban nem vizsgálunk. Ez ugyanaz, mint kiválasztani hetet. Maradjunk az utóbbinál. A hétből kettőt, amelyikben nincs golyó, elveszünk, marad öt doboz. "A" jelentse azt az eseményt, hogy a maradék öt dobozban legalább egy golyó van. Utóbbi úgy valósulhat meg, ha a dobozokban pontosan két golyó van, illetve úgy is, hogy a dobozokban pontosan egy golyó van.
Ennyi inspiráció elegendő?
|
| Előzmény: [671] Alma, 2013-01-18 18:45:49 |
|
|





 {0,1} függvény, legyen F ezen függvények halmaza. Adott x
{0,1} függvény, legyen F ezen függvények halmaza. Adott x I-re az x ember
I-re az x ember  x stratégiája egy
x stratégiája egy