| [704] Maga Péter | 2013-01-28 20:25:14 |
 Nem egészen értek egyet.
Abban teljesen igazad van, hogy használunk más axiómákat is.
Ugyanakkor a kiválasztási axiómát egy kicsit szokás külön kezelni. Nem vagyok sem halmazelmélész, sem logikász, de azt ellestem a halmazelmélészektől és logikászoktól, hogy a 'kivax' azért speciális. Nem értek hozzá, nem tudom, miért van így, de ha valami megy kiválasztási axióma nélkül, akkor azt igyekeznek nélküle megcsinálni, és csak akkor használják a kiválasztási axiómát, ha muszáj. Több tétel állítását is hallottam már úgy, hogy 'kiválasztási axióma mellett igaz az, hogy ...' -- a többi axiómát nem hangsúlyozva.
Egy egyetemi emlékem a következő. Móri Tamás tanár úr (pedig ő valószínűségelmélész, tehát nem a matematika alapjaival foglalkozik) egy valószínűségszámítási tételnél megjegyezte, hogy kiválasztási axiómával könnyen kijön, aztán nekiállt egy nehezebb bizonyításnak, mondván hogy az a pofonegyszerű kiválasztási axiómás érvelés ,,úri huncutság''. A végtelen halmazok sohasem zavarták.
-----
Ott van Wedderburn tétele: minden véges ferdetest kommutatív. És ha valaki megkérdezné tőlem, hogy ez min múlik, akkor azt mondanám, hogy a végességen. Pedig ugyanúgy szükségünk van a ferdetest axiómáira, de azok inkább a nyelvét teremtik meg a tételnek. A feladat megoldása ZFC-ben történik, és igazából C-n múlik; ZF nélkül a feladatot el se tudnánk mondani, arra már a terminológia miatt is szükségünk van (ha nem is ZF összes axiómájára).
És persze ebben van önkényesség.
|
| Előzmény: [703] Micimackó, 2013-01-28 18:25:31 |
|
| [703] Micimackó | 2013-01-28 18:25:31 |
 Ez a példa csak akkor megrázó, ha az ember elvárja hogy a végesben megszokott dolgok végtelenben is működjenek. És ez a feladat is olyan, hogy ha valaki meghallgatja a megoldást is, nem csak az eredményt, már egyből természetesebbnek tűnik, hogy így van (persze az előtt én is a másikra tippeltem volna).
Én sosem tartom jogosnak amikor az ilyesmit a "kiválasztási axióma következményének" titulálják. A bizonyítás sok másik axiómát is felhasznál, amiket ilyen alapon ugyanúgy lehetne vitatni. Például a végtelenségi axióma sokkal kevésbé szemléletes (bizonyos értelemben antiszemléletes, mert nincsenek végtelen dolgok igazából), mégis mindenki elfogadja. Szóval tessék csak megbékélni az axiómákkal és nem bolygatni őket.
|
| Előzmény: [702] Maga Péter, 2013-01-28 09:11:08 |
|
| [702] Maga Péter | 2013-01-28 09:11:08 |
 Egy megjegyzés. További érdekesség, hogy sehol nem használjuk azt, hogy két lehetőség van minden egyes sapka színére. Tehát ha mindenki homlokára akár egy valós számot írnak, és mindenkinek a saját számára kell tippelnie, akkor is elérhető, hogy csak véges sokan tévedjenek. Ez már végképp sokkoló.
Számomra ebben a feladatban elsőre az volt az igazán meglepő, hogy az ártatlannak és szemléletesnek kinéző kiválasztási axiómának ilyen természetellenes következményei vannak. A kiválasztási axiómát olyan dolgokra használjuk általában, hogy 'minden vektortérnek van bázisa', vagy hogy 'van nem Lebesgue-mérhető halmaz a számegyenesen'. Ez a példa azoknál sokkal megrázóbb, pedig sokkal egyszerűbb.
|
| Előzmény: [701] Micimackó, 2013-01-27 21:13:23 |
|
| [701] Micimackó | 2013-01-27 21:13:23 |
 Az a lényeg, hogy a "csak véges sokban tér el" ekvivalencia reláció, így osztályokra bonthatjuk a sapka kiosztásokat úgy, hogy egy csoportban a kiosztások csak véges sokban térnek el.
Ezek után minden ilyen osztályból kitüntetünk egy elemet (ezt megtehetjük, ennek halmazelméleti okai vannak). Mikor egy játékos szétnéz, akkor el tudja dönteni melyik osztályba esik a kiosztás. Azt a színt tippeli, amilyen színű a sapkája az osztály kitüntetett kiosztásában. Mivel így pont az osztály kitüntetett kiosztását fogják tippelni, és az csak véges sokban tér el az aktuális kiosztástól, így csak véges sokan tévednek.
Módosítás a feladathoz: Ki tudnak-e találni egy olyan stratégiát, amelynek segítségével legfeljebb c ember hal meg? (azaz van-e olyan c, amivel igen a válasz; ha van, akkor mi a legkisebb)
|
| Előzmény: [700] Maga Péter, 2013-01-27 10:52:08 |
|
|
| [699] Micimackó | 2013-01-27 10:21:14 |
 No igen, ez már jogosnak tűnik. Akkor mivel időközben azt is elárultad, hogy van stratégia, ahhoz egy ötlet: ha valaki véges sok kéket lát, mondjon pirosat, ha véges sok pirosat, akkor mondjon kéket. Ez megoldja az ilyen eseteket. A többi esetben is valami ilyesmit kéne csinálni: venni kitüntetett helyzeteket, és ha attól csak véges sokban tér el amit látsz, akkor ahhoz igazodva mondasz (ilyen volt a spec esetben a csupa kék és a csupa piros).
|
| Előzmény: [698] Maga Péter, 2013-01-26 21:26:33 |
|
| [698] Maga Péter | 2013-01-26 21:26:33 |
 Tegyük fel, hogy X alkalmaz valami stratégiát!
Az 1/2 valószínűség [691]-es hozzászólásod értelmében az, hogy
P(X túlél|X a többieken ...-ot lát)=1/2.
Hogyan következik ebből, hogy
P(X túlél)=1/2?
A [691]-ben előbbi mellett érvelsz, aztán [697]-ben utóbbit használod. Pedig az 'X a többieken ...-ot lát' olyan események ('...' befutja az összes lehetségest), amik mind 0 valószínűségűek, tehát nem lehet csak úgy utóbbira következtetni az előbbiből.
|
| Előzmény: [697] Micimackó, 2013-01-26 19:00:40 |
|
| [697] Micimackó | 2013-01-26 19:00:40 |
 (Attól mert nem valószínűségszámítás feladat, használható a megoldásban valószínűség számítás.) Természetesen nem függetlenek az elbukási események, ezt sosem állítottam. De a bukási esélyek 0.5-ök fejenként. Így érvényes amit írtam: Annak az esélye, hogy "végtelen sok 0.5-os esemény közül csak véges sok esemény következik be" maximum 0.5 lehet (a feladat meg azt kérdezi lehet-e ez a biztos esemény, ami pedig 1 valószínűségű).
|
| Előzmény: [695] Maga Péter, 2013-01-26 18:33:06 |
|
| [696] w | 2013-01-26 18:38:24 |
 Minden rab csak annyit lát, hogy kinek mi van a fején, és ha egyszerre tippelnek, és nem jelezhetnek egymásnak, akkor függetlenül tippelnek. Mindenki tehát max. azt szűri le, hogy milyen színből van több, és azt tippeli, ezzel mindenki a többször szereplő színt tippeli be, és többen szabadulnak, mint halnak. (Az sem túl stabil, hogy végteleneket hasonlítgatunk össze, de ez mellékes.) Viszont az is lehet, hogy kékből és pirosból is végtelen sok van (lásd modulo 3 maradékosztályok), és akkor végtelen sokan halnának meg. Tehát nincs jó stratégia? Az én részemről szabad a gazda.
|
| Előzmény: [694] Maga Péter, 2013-01-26 18:18:35 |
|
| [695] Maga Péter | 2013-01-26 18:33:06 |
 Akár egymástól függetlenül sorsolják a sapkákat, akár nem, az elképzelt stratégiában a rabok nyilván nem egymástól függetlenül* tippelnek. Emberünk persze -- mint mindenki más -- 1/2 eséllyel elbukik, de ezek az elbukások nem független események.
* 'nem egymástól függetlenül': a valószínűségi értelemben értendő; a szabályoknak megfelelően persze nem használják egymás tippjeit, tehát ebben persze egymástól függetlenül, de nem erről beszélek
-----
A nagy félrecsúszás elkerülése céljából: ez egy logika (vagy tetszés szerint halmazelmélet) feladat, nem valószínűségszámítás. Kicsit sok volt a Monty Hall, ennek a feladatnak semmi köze a valószínűségekhez. Nyilván egy valószínűségi módszert használó rossz megoldás valószínűségi hibát vét, csak azért valószínűségeztem, hogy ezt elmagyarázzam.
|
| Előzmény: [691] Micimackó, 2013-01-26 17:41:29 |
|
|
| [693] Maga Péter | 2013-01-26 18:14:51 |
 Ha véges számú rabról van szó, akkor minden stratégiára igaz, hogy tetszőleges sapkakiosztás után véges sokan veszítenek. A konkrét stratégiát is le lehet hozni véges sok ember esetére (bár elég semmitmondó lesz).
|
| Előzmény: [692] HoA, 2013-01-26 17:46:07 |
|
|
| [691] Micimackó | 2013-01-26 17:41:29 |
 Szerintem ez mindenképpen igaz, ha feltesszük, hogy a sapkákat egymástól függetlenül sorsolják (amit feltehetünk): Ekkor emberünk a többiek fején lát valamit, ez alapján tippel valamit (mondjuk kéket), de 0.5 eséllyel piros van a fején.
|
| Előzmény: [690] Maga Péter, 2013-01-26 15:08:19 |
|
| [690] Maga Péter | 2013-01-26 15:08:19 |
 ,,(...) minden ember 0.5 eséllyel téveszti el a sapkája színét.''
Ha véletlenszerűen tippel, akkor ez igaz. Segítség: a többiek sapkáját látva mindenki le tud szűrni egy elég természetellenes információt. Mi lehet az?
|
| Előzmény: [689] Micimackó, 2013-01-26 12:45:48 |
|
| [689] Micimackó | 2013-01-26 12:45:48 |
 Úgy sejtem nem lehet, hiszen minden ember 0.5 eséllyel téveszti el a sapkája színét. Annak az esélye, hogy "végtelen sok 0.5-os esemény közül csak véges sok esemény következik be" maximum 0.5 lehet.
|
| Előzmény: [682] Maga Péter, 2013-01-19 12:52:56 |
|
| [688] Micimackó | 2013-01-26 12:22:49 |
 "Itt értem a "stratégia" jelentését, hiszen mindenki a már elhangzott tippek és az előtte látható sapkák alapján alakíthatja tippjét." - A stratégia itt is ugyanazt jelenti, de itt a tipp, csak a többiek sapkájától függhet: az emberek meg vannak számozva, és tudod hányas számúnak milyen színű a sapkája, kivéve a sajátod.
|
| Előzmény: [686] HoA, 2013-01-25 20:58:56 |
|
| [687] Maga Péter | 2013-01-25 22:27:22 |
 A következőt értjük stratégia alatt. A piros és kék sapkát röviden rendre 0-val, illetve 1-gyel jelölöm.
Legyen az emberek halmaza I, egy adott sapkakiosztás pedig egy f:I {0,1} függvény, legyen F ezen függvények halmaza. Adott x {0,1} függvény, legyen F ezen függvények halmaza. Adott x I-re az x ember I-re az x ember  x stratégiája egy x stratégiája egy  x:F x:F {0,1} függvény, melyre teljesül, hogy ha f és g csak az x-ben térnek el, akkor {0,1} függvény, melyre teljesül, hogy ha f és g csak az x-ben térnek el, akkor  x(f)= x(f)= x(g) ('saját magát nem látja'). x(g) ('saját magát nem látja').
Egy  stratégia ezek összessége, tehát egy függvény I×F-ről {0,1}-be, mely minden egyes x stratégia ezek összessége, tehát egy függvény I×F-ről {0,1}-be, mely minden egyes x I-re konstans az F-beli függvény x feletti megváltoztatása során, azaz I-re konstans az F-beli függvény x feletti megváltoztatása során, azaz  (x,f)= (x,f)= (x,g), ha minden x-től különböző y (x,g), ha minden x-től különböző y I-re f(y)=g(y). I-re f(y)=g(y).
A kérdés pedig az, hogy van-e olyan  , hogy , hogy  (x,f)=f(x), minden egyes f (x,f)=f(x), minden egyes f F-re legfeljebb véges sok x kivételével. F-re legfeljebb véges sok x kivételével.
|
| Előzmény: [686] HoA, 2013-01-25 20:58:56 |
|
| [686] HoA | 2013-01-25 20:58:56 |
 Azt ismerem, ahol n db ( végses számú ) rabot a fejükre húzott kék és piros sapkákkal egymás mögé sorba állítanak, tehát mindenki látja az összes előtte álló sapkáját, de nem látja a sajátját és a mögötte állókét. A leghátsó mond egy tippet a saját sapkája színére, amit mindenki hall, majd az előtte álló, és így tovább. Itt értem a "stratégia" jelentését, hiszen mindenki a már elhangzott tippek és az előtte látható sapkák alapján alakíthatja tippjét. De hogyan beszélhetünk stratégiáról, ha egyszerre kell tippelni? Persze lehet, hogy a végtelennel van a turpisság.
|
| Előzmény: [682] Maga Péter, 2013-01-19 12:52:56 |
|
| [685] Fálesz Mihály | 2013-01-21 20:36:46 |
 Egy másik, a Csaszi bácsi féle Analízis Tanszék régi stenciljeinek idejéből származó gyakorlat.
Tagadjuk a következő állítást:
| ,,Minden asszony életében jön (van) egy pillanat, mikor olyat akar tenni, amit nem szabad.'' (Hofi) |
|
(Írjuk fel kvantorokkal, tagadjuk, majd fogalmazzuk meg a tagadást szövegesen is. Végül zenésítsük meg.)
|
|
|
|
| [682] Maga Péter | 2013-01-19 12:52:56 |
 Új feladat. Aki már hallotta, de lője le!
Egy börtönben (mondjuk megszámlálhatóan) végtelen sok rabot őriznek. Egy alkalommal a következőt ajánlják fel nekik. Mindegyiküknek a fejére tesznek egy piros vagy kék sapkát, ezután a többiek sapkáját látva (de a sajátjukat nem) mindannyiuknak egyszerre tippelnie kell a saját sapkájának színére. Aki eltalálja, azt szabadon engedik, aki nem találja el, azt kivégzik.
A rabok megbeszélhetnek egy stratégiát. Ki tudnak-e találni egy olyan stratégiát, amelynek segítségével véges sok kivételtől eltekintve mind kiszabadulnak?
|
|
|
| [680] Ménkűnagy Bundáskutya | 2013-01-18 23:08:30 |
 Úgy számoltam, hogy rendre 6/90, 42/90, 42/90 valséggel van 2, 1, 0 kulcs az elsőként kiválasztott három dobozban. Onnan rendre 0, 1/5, 2/5 valséggel nyerünk, tehát összesen 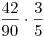 esélyünk van, ami annyi, amennyi. esélyünk van, ami annyi, amennyi.
Tényleg nem értettem teljesen, mit akarsz. Kicsit igen, azért emeltem ki a 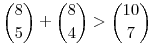 -t. -t.
|
| Előzmény: [679] Solaris, 2013-01-18 22:39:16 |
|






 {0,1} függvény, legyen F ezen függvények halmaza. Adott x
{0,1} függvény, legyen F ezen függvények halmaza. Adott x I-re az x ember
I-re az x ember  x stratégiája egy
x stratégiája egy 

