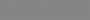| [1812] Lacczyka | 2007-01-25 15:46:51 |
 Az említett feladatot nem ismerem, légyszi tedd fel ide, vagy küldd el mailben (lacczyka@freemail.hu). Előre is köszi szépen :)
|
|
|
| [1810] jonas | 2007-01-25 11:30:16 |
 Pontosan.
Továbbá van a csalfa nőknek egy változata gőzmozdonnyal, és egy sapkákkal. A sapkás változatot valamelyik Smullyan könyv is említi.
|
| Előzmény: [1809] HoA, 2007-01-25 10:29:44 |
|
|
|
| [1807] rizsesz | 2007-01-24 20:25:05 |
 Azt érdemes végiggondolni, hogy mi a helyzet akkor ha páros, vagy ha páratlan sok oroszlán van. Igazából ki kell találni, hogy 2 oroszlánnál mi van, és akkor ebből hogyan következtethető ki a 3 oroszlán helyzete, stb.
|
|
| [1806] Lacczyka | 2007-01-24 18:51:15 |
 Üdv!
Igazából segítséget szeretnék kérni. Még régen találkoztam ezzel a feladattal:
Egy szigeten él 23 oroszlán. Ezek az oroszlánok teljesen civilizáltak (egymást "élve" nem eszik meg), okosak (képesek elvont gondolkodásra), és nemutolsósorban nagyon éhesek, lévén hogy a szigeten rajtuk kívül nincsen semmi.
Néhány galád kutató kísérleti jelleggel elhelyez a sziget közepén egy adag mérgezett húst (a galád kutatók a feladat szempontjából nem ehetőek), és várják, hogy az oroszlánok megeszik-e. A méreg hatása az, hogy amelyik oroszlán megeszi, az elalszik, de nem hal éhen. Ha viszont elaludt, akkor inenstől kezdve őt is megehetik az oroszlántársai, ebben az esetben azonban az az oroszlán, aki megeszi őt, szintén elalszik. Röviden: ha egy oroszlán megeszi a mérgezett húst, akkor életben marad, viszont mostantól mérgezett húsként funkcionál.
Az oroszlánok okosak, tudják, hogy a hús mérgezett, és a következő elvek alapján döntenek: 1, semmilyen körülmények között nem akarnak megevődni, vagyis inkább éhenhalnak, minthogy valaki őket netán elfogyassza. 2, életben akarnak maradni, vagyis ha nem fenyeget veszély, akkor megeszik a húst, és elalszanak.
Mit fog tenni az az oroszlán, amelyik először ér oda a húshoz: megeszi-e, vagy sem?
A feladat nem túl nehéz. Igazából hasonló típusú feladatokat szeretnék gyűjteni. Hogyha van valakinek olyan feladata, ami ehhez megoldásában, vagy gondolkodásmódjában hasonlít, akkor az legyen szives elküldeni nekem.
Előre is köszi: Lacczyka
|
|
|
| [1804] sakkmath | 2007-01-22 11:22:22 |
 A komoly problémák után kikapcsolódásként következzék egy könnyedebb, humoros feladat, amely Áprilisi fejtörő címmel a KöMaL 1980/4. számában jelent meg Csirmaz Lászlótól.
|
 |
|
|
| [1802] epsilon | 2007-01-21 09:08:31 |
 Köszi Mindenkinek! Alaposan kimerítettétek a témát! ;-) Cchek: a két szöget x illetve y-ra nevezve, mindkét oldalt 4-gyel szorozva, a sin2x=2sinx×cosx alapján, nullára rendezve, két négyzetösszek különbsége szorzatra bomlik és ez a 2 eset áll elő: sin2x=-2ctgy illetve sin2x=2ctgy és most a sin2x-et a tangens felesképletekkel kifejezzük sin2x=2t/(1+t×t) ahol t=tgx és így t-ben másodfokú egyenlet lesz, szerinted ez az út nem járható?
|
|
| [1801] Lóczi Lajos | 2007-01-20 23:54:31 |
 A számítógép szépen végignézte az összes esetet, és persze megtalálta a (100,0,0,0,0,0), (50,50,50,50,0,0) optimumokat (és csak ezeket találta).
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1800] Lóczi Lajos | 2007-01-20 21:32:49 |
 Ó, persze, a nemnegativitási feltételeket kihagytam. Köszönöm, hogy rámutattál.
(Az zavarhatott meg, hogy egyenlőtlenséggel megadott feltételek esetén a multiplikátoroknak maguknak is nemnegatívnak kell lenniük, de ez még nem mond semmit a változókról...)
|
| Előzmény: [1799] HoA, 2007-01-20 19:43:10 |
|
| [1799] HoA | 2007-01-20 19:43:10 |
 A megfigyelt jelenség már akkor is előjön, ha csak az első feltételt vesszük. Legyen tehát
L(x,y, ):=x2+y2+ ):=x2+y2+ (100-x-y) (100-x-y)
Az első két parciális deriváltból itt is kijön x=y. Ábrázoljuk az f(x,y)=x2+y2 függvényt az xy síkban szintvonalakkal: ezek nyilván origó középppontú koncentrikus körök. A vizsgált tartomány az x+y=100 egyenes által határolt félsík. f(x,y) a tartományban és a határán is tetszőleges nagy értéket felvehet, maximuma nincs. Az egyenes x=0 vagy y=0 értékkel jellemzett pontja, amelyekből az y=100 ill. x=100 érték adódna, semmilyen különleges szerepet nem játszik. Nem is csoda, hiszen nemcsak x és y nagyságviszonyát, hanem az x 0 , y 0 , y 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul: 0 feltételeket sem vettük figyelembe. Ha megtesszük, a Lagrange függvény így alakul:
L(x,y, 1, 1, 2, 2, 3):=x2+y2+ 3):=x2+y2+ 1(100-x-y)+ 1(100-x-y)+ 2(x-0)+ 2(x-0)+ 3(y-0) 3(y-0)
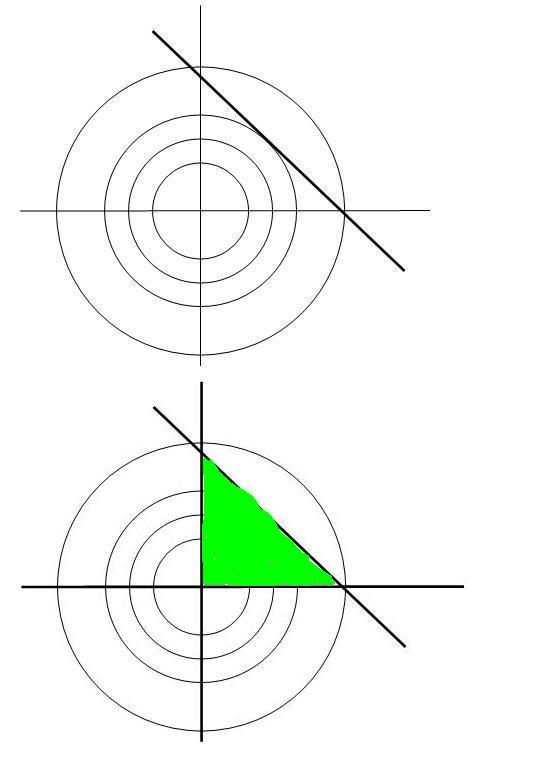
A megoldandó egyenletrendszerben a 0-t adó szorzatoknál 0 tényezőül {100-x-y=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 2=0;y=0} -t választva x = 100, {100-x-y=0;x=0; 3=0} -ból y = 100 adódik. A { 3=0} -ból y = 100 adódik. A { 1=0;x=0;y=0} választás a megengedett 1=0;x=0;y=0} választás a megengedett  alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w 100 és z+t+u+w 100 mellett a w 100 mellett a w 0 , u 0 , u w , t w , t u, ... , x u, ... , x y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt. y feltételeket is figyelembe kell venni. Ezzel egyúttal a változók nemnegatív voltát is biztosítjuk. A 8 db 0 szorzat 0 tényezőinek megválasztásánál - 28 eset - anélkül, hogy mind a 256 kombinációt végignéznénk, csak rámutatunk, hogy a { w=0; u=w ; t=u; z=t ; y =z ; x+y = 100 } választás adja az x=100,y=z=t=u=w=0 megoldást, míg a { w=0; u=w ; z=t ; y =z ; x+y = 100 ; z+t+u+w = 100 } kombináció az x=y=z=t=50,u=w=0 eredményt.
|
 |
| Előzmény: [1791] Lóczi Lajos, 2007-01-19 01:16:58 |
|
|
| [1797] HoA | 2007-01-19 23:04:07 |
 A módszer az alábbi általánosításig biztosan működik:
- a két csoportban szereplő számok darabszáma ( most 2, ill. 4 ) legyen k ill. m.
- a csoportok elemeinek összege ( most 100,100) ne legyen nagyobb, mint A ill. B
Tehát legyen k+m számunk, x1,...,xk+m , ahol
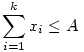 | (2) |
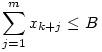 | (3) |
Mekkora 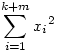 maximuma? maximuma?
Az összeget rögzített xk (az első csoport legkisebb eleme, az eddigi y) mellett vizsgáljuk. (1) -ből és (2) -ből 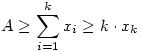 , , 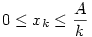 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 ( Ez egyben válasz Epsilon kérdésére: A=100 és k=2 esetére 0 x2=y x2=y 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 50 ) Az [1795]-beli indokláshoz hasonlóan belátható, hogy az első csoport négyzetösszege akkor a legnagyobb, ha x2=x3=...=xk x1=A-(k-1).xk Példa: ha k=4,x4=4,A=22 , akkor { 10;4;4;4 } négyzetösszege nagyobb, mint pl. { 7;6;5;4 } -é. A második csoportra igaz az [1795]-beli szabály: ameddig lehet xk+j=xk egy szám pedig B és az eddigiek összegének különbsége: xk+1=xk+2=...=xk+d=xk,xk+d+1=B-d.xk Az [1795]-beli szakaszhatárok most a 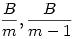 ... értékek. Vegyük észre, hogy ... értékek. Vegyük észre, hogy 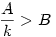 esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha esetén xk>B is előfordulhat, tehát maga B is lehet szakaszhatár. Ekkor a második csoport első eleme B, a többi 0. Másrészt ha 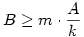 akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom. akkor a második csoportba mindig "belefér" m darab xk érték, tehát görbénk csak egyetlen parabolaívből áll. Függvénygörbénk - a maximális négyzetösszeg xk tól függése - vizsgálatát másokra hagyom.
|
| Előzmény: [1796] epsilon, 2007-01-19 17:09:25 |
|
| [1796] epsilon | 2007-01-19 17:09:25 |
 Helló HoA! Valóban elemi, logikus, szép. Van néhány kérdöjelem, amit magamban kellene tisztáznom: Az y nem több mint 50 az indulásból feltehető? Továbbá ha általánosítani kellene, a 100 helyett pl. 2a lenne, na meg a tagok száma 6 helyett n, akkor az általad jelzett 3 intervallumba sorolás az y-ra vonatkozóan hogyan alakulna, mindegyiket külön-külön elemezni kellene, vagy belátható-e elég könnyen, hogy a sok lokális maximumból melyik is a globális maximum? Én ezeken tűnődöm, ha vannak megjegyzéseid, szívesen veszem, és kösz, a megoldásodban volt jó pár mentő ötlet! Üdv: epsilon
|
|
| [1795] HoA | 2007-01-19 11:20:58 |
 Egy elemi eszközöket használó megoldás lépései:
Bontsuk a négyzetösszeget két részre, legyen az első tag x2+y2 , a második z2+t2+u2+w2 . Vizsgáljuk a maximumot rögzített y mellett (0 y y 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 . 50). Az első tag nyilván akkor a legnagyobb, ha x = 100 - y. A második tagban keressük négy 0 és y közötti z,t,u,w szám maximális négyzetösszegét, ahol z+t+u+w<=100 .
1) Belátható, hogy ha z+t+u+w<100 és nem mindegyik = y, akkor az y-nál kisebb számok növelésével a négyzetösszeg nő.
2) Belátható, hogy rögzített z+t+u+w mellett a négyzetösszeg nő, ha egy nagyobb számot növelünk és egy kisebbet csökkentünk: Szabatosan : Ha z>t d>0, akkor (z+d)2+(t-d)2>z2+t2 d>0, akkor (z+d)2+(t-d)2>z2+t2
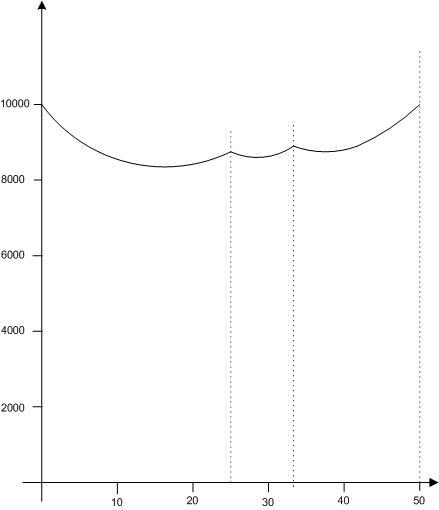
1) -ből és 2) -ből következik, hogy a második tag akkor a legnagyobb, ha z,t,u,w ameddig csak lehet = y , egy szám pedig a többiek 100-ból vett maradéka. Vagyis a második tag szerkezete függ y-tól. Szabatosan: Ha 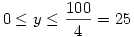 , akkor a második tag maximuma 4y2 , a két tag összege , akkor a második tag maximuma 4y2 , a két tag összege
. Ha 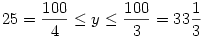 , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege , akkor a második tag maximuma 3y2+(100-3y)2 , a két tag összege
| (100-y)2+4y2+(100-3y)2 | (2) |
. Végül ha 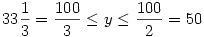 , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege , akkor a második tag maximuma 2y2+(100-2y)2 , a két tag összege
| (100-y)2+3y2+(100-2y)2 | (3) |
A négyzetösszeg maximumot y függvényében ábrázolva tehát egy három, egymáshoz csatlakozó, alulról konvex parabolaívből álló görbét kapunk. A teljes y tartományra a maximumot ezért csak a széleken és a csatlakozási pontokban kell vizsgálni. természetesen a már ismert eredményt kapjuk: A maximum 10000, amit az x=100, y=z=t=u=w=0 és az x=y=z=t=50, u=w=0 értékrendszerek adnak.
|
 |
| Előzmény: [1792] epsilon, 2007-01-19 07:16:56 |
|
| [1794] epsilon | 2007-01-19 11:16:20 |
 Szerintem nem, mert ennél nem használtuk fel a betűk közötti rendezési sorrendet, és ha annélkül kijönne, akkor...nem stimmel mert a feltételek nélkül más értékekre nagyobb lehet a maximum. Vagyis akár rendezett sorrenddel, akár annélkül, nem jöhet ki ugyanaz.
|
|
| [1793] Cckek | 2007-01-19 10:15:30 |
 Nos a kérdésem az, hogy ezen feltételek mellett fennáll-e a
(x+y+z+t+u+w)2+(x-y)2+(x-z)2+(x-t)2+(x-u)2+(x-w)2+(y-z)2+(y-t)+(y-u)2+(y-w)2+(z-t)2+(z-u)2+(z-w)2+(t-u)2+(t-w)2+(u-w)2 6.1002 egyenlőtlenség? Ugyanis ekkor a Lagrange azonosságból következik a maximum. 6.1002 egyenlőtlenség? Ugyanis ekkor a Lagrange azonosságból következik a maximum.
|
| Előzmény: [1791] Lóczi Lajos, 2007-01-19 01:16:58 |
|
| [1792] epsilon | 2007-01-19 07:16:56 |
 Egy biztos: a feladatot olyan helyen találtam, hogy elemi eszközökkel gondoltak a megoldására. Ahogy viccese mondják, ezt analízissel megoldani olyen mint a bolhavadászat fejszével :-) Az alapelgondolásom az volt (az y-nál kisebb rendett számok miatt), hogy mivel előtte csak 1 szám van, nála kisebb meg 4 szám, ezért az x maximizálása sokkal gyengébb mint az y maximizálása, ami által a többi 4 szám maximizálható, és ezeket maximizálva jobban közeledünk a négyzetösszeg maximumához. Valahogyan nem illik ebbe a képbe a 100, és a többi 0 megoldás. Persze mindez csak érzés, sejtés, de...???
|
|
| [1791] Lóczi Lajos | 2007-01-19 01:16:58 |
 Felírtam a feltételeket, de nem jött ki csak 7500 a maximum értékére. Valaki tudna segíteni, hogy megértsem, miért nem kaptam meg a 10000-et?
Tehát a link azt mondja, írjam fel a feladat Lagrange-függvényét (az ottani  1 és 1 és  2 helyett 2 helyett  és és  betűket használtam): betűket használtam):
L(x,y,z,t,u,w, , , ):=x2+y2+z2+t2+u2+w2+ ):=x2+y2+z2+t2+u2+w2+ (100-x-y)+ (100-x-y)+ (100-z-t-u-w). (100-z-t-u-w).
Ekkor a lehetséges maximum helyét az alábbi egyenlet-egyenlőtlenségrendszer megoldása adja (az alsó indexek a megfelelő parciális deriváltakat jelöljék, az L függvény argumentumait nem írom ki):
Lx=0,Ly=0,Lz=0,Lt=0,Lu=0,Lw=0, (100-x-y)=0, (100-x-y)=0, (100-z-t-u-w)=0, (100-z-t-u-w)=0,  0, 0,  0. 0.
Igen ám, de az első két egyenletből az jön ki, hogy x=y, és így rögtön kiesett x=100,y=z=t=u=w=0 megoldás.
Hol van vajon az ellentmondás oka? (A változók nagyság szerinti rendezésére vonatkozó feltételt egyelőre elhagytam az eredeti feladatból.)
|
| Előzmény: [1790] Lóczi Lajos, 2007-01-19 00:00:48 |
|
|
| [1789] Lóczi Lajos | 2007-01-18 23:55:45 |
 Le tudnád írni a multiplikátor-elvet ebben a szituációban, amikor egyenlőtlenségek is szerepelnek a feltételi halmaz kijelölésében? Vagy egy online hivatkozást esetleg, hogy szisztematikusan megpróbáljuk kiszámolni a kérdést.
|
| Előzmény: [1786] Cckek, 2007-01-18 20:44:15 |
|
|
| [1787] epsilon | 2007-01-18 21:50:05 |
 Bocs, a pötyögtetéssel elírtam :-( ezeket: x+y>=100, z+t+u+w>=100 helyesen így lenne: x+y<=100, z+t+u+w<=100 na meg nem szándékom nagyágyúval rálőni, mert több változóra, 100 helyett másra is, meg 6 szám helyett szerintem többre is a 100,0,0,0,0,0 illetve az 50,50,50,50,0,0 esetekben érné el a maximumot? De alaposabban indokolva? Vagy van más vélemény?
|
|
|
|
| [1784] HoA | 2007-01-18 08:34:51 |
 Szia Epsilon!
Lóczi Lajosnak igaza van, így a feladat érdektelen. Viszont amúgy érdekelne, légy szíves nézd meg, ahol "összefutottál" vele, hogy is állnak valójában az egyenlőtlenségjelek.
|
| Előzmény: [1772] epsilon, 2007-01-17 14:15:21 |
|
|
| [1782] Matthew | 2007-01-17 21:32:55 |
 Bocsánat,Neked van igazad,én az állításból kifolyólag egyértelműnek tartottam,hogy ha a 2-es hátlapján 4-es van,akkor a 4-es kártya hátlapján 2-es van,és ezért elég csak az 1,3-at megfordítani....Becsapós,a 4-esen buktam el a dolgot...Cserébe itt egy feladat(bár igazság szerint a "Csak logika"topikba kellene írnom):
Van 100 cédula. Az elsőre azt írták, hogy "pont egy cédulára írt állítás hamis". A másodikra azt, hogy "pont két cédulára írt állítás hamis", és így tovább. A századikon ez áll:"pont száz cédulára írt állítás hamis". Vajon hány cédulán áll igaz állítás?
|
| Előzmény: [1774] Sirpi, 2007-01-17 14:25:30 |
|
| [1781] Lóczi Lajos | 2007-01-17 21:29:17 |
 Köszönöm ezt a szép eszmefuttatást! Meglepett, hogy "véges dimenzióban" meg lehetett oldani a kérdést szakaszonként lineáris függvényekkel (a töréspontokban persze hajszálnyit lekerekítve, hogy a sebességgrafikon ne törjön meg -- amúgy vajon van annak fizikai realitása, hogy megtörik? Mondjuk ütközésnél talán lehetne feltételezni ezt, nem?) Azért féltem, hogy nehéz ez a kérdés, mert azt hittem, igazi "görbékkel" kell majd dolgozni, de ezt megcáfoltad :)
|
| Előzmény: [1766] Sirpi, 2007-01-17 07:56:06 |
|
| [1780] Lóczi Lajos | 2007-01-17 20:25:25 |
 A 6 szám négyzetösszege akármilyen nagy lehet, írj be pl. egymillió körüli értékeket a változók helyére. De a gondolatmenetedből az látszik, hogy bizonyos egyenlőtlenségjelek meg vannak fordítva, szóval két különböző feladatról beszélünk.
|
| Előzmény: [1772] epsilon, 2007-01-17 14:15:21 |
|
| [1779] Roberto85 | 2007-01-17 17:34:24 |
 na mind1 közben rájöttem a megoldásra nagyon köszi ha valaki gondolkodott rajta
|
|
| [1778] Roberto85 | 2007-01-17 16:05:41 |
 erre valaki? a, Van egymás mellett 5 ház, mind az 5 különböző színű b, A házakban egy egy személy lakik, mind különböző nemzetiségű c, MIndegyik fogyaszt valamilyen italt, dohányárút és tart valamilyen álatot. d, Egyikük sem fgyaszt ugyanolyan italt, szív ugyanolyan cigit, és tart ugyanolyan állatot.
Egyéb információk: 1. Brit piros házban lakik 2, svéd kutyát tart. 3. Dán teát iszik 4. fehér ház balján a zld ház van. 5, a zöld házban kávét fogyasztanak. 6. Az a személy aki Pall mallt szív, madarakat tart. 7. sárga ház lakója Dunhillt szív 8. Középső házban lakó tejet iszik 9. norvég az első házban lakik. 10.a Blendet szívó szomszédjában lakó macskát tart. 11. A blue mastert szívó ember sörözik 12.A lovakat tartó szomszédjábanlakó Dunhillt szív. 13. A német Prince-t szív 14. A norvég a kék ház szomszédja 15A blendet szívó ember szomszédjban vizet isznak
|
|
| [1777] i | 2007-01-17 15:29:31 |
 Ebben az esetben a 2-est és a 4-est kell megfordítani, mert csak akkor lehet igaz az állítás az összes kártyára, ha a kettes hátoldalán 4-es van, a négyesén pedig kettes (egy kártya biztosan nem elég, minden esetre lehet példát találni).
|
| Előzmény: [1774] Sirpi, 2007-01-17 14:25:30 |
|
| [1776] jonas | 2007-01-17 15:28:45 |
 Pontosan.
Ez hasonlít ahhoz a kártyás feladathoz, amit Mérő valamelyik könyvében leír, csak ott ki van kötve, hogy minden kártyának az egyik oldalán 1 vagy 2 és a másik oldalán 3 vagy 4 van. Ilyenkor a 2-t és a 3-at kell megfordítani, de az 1-et és a 4-et nem.
|
| Előzmény: [1774] Sirpi, 2007-01-17 14:25:30 |
|
| [1775] psbalint | 2007-01-17 14:26:28 |
 ajaj, lehet hogy jobban bele kellett volna gondolnom :)
|
|
| [1774] Sirpi | 2007-01-17 14:25:30 |
 De ha a 2-est nem fordítod meg, honnan tudod, hogy 4-es van-e a hátulján? És az 1,3-at pedig azért kell megfordítani, hátha 2-es van a másik oldalukon, ami cáfolná az állítást. A 4-est nem kell megfordítani: akár 2-es van a hátulján, akár nem, egyik esetben sem cáfolja az állítást, tehát a többi kártyán múlik, hogy az igaz-e.
Mondjuk érdekesebb lenne a probléma, ha a kártyák hátulján is az 1-4 számok permutációja szerepelne és ezt tudnánk... Egyelőre nem gondoltam még át, hogy ilyenkor hogy érdemes fordítgatni.
|
| Előzmény: [1773] Matthew, 2007-01-17 14:19:50 |
|
| [1773] Matthew | 2007-01-17 14:19:50 |
 Üdv!
Ha szabad,én is vitatkoznék ezzel egy kicsit(nézzétek el nekem,ha sületlenséget írok,én még nem vagyok azon a szinten matekból,mint ti,de ezt megpróbálnám).
Tehát:Ha az az állítás,hogy ha a kártya egyik oldala 2-es,akkor a másik 4-es,akkor szerintem pont azokat kellene megfordítani,amelyekre nem vonatkozik az állítás,vagyis az [1],[3]-at,hogy bebízonyítsuk az állítást.
|
| Előzmény: [1771] Sirpi, 2007-01-17 13:58:53 |
|
| [1772] epsilon | 2007-01-17 14:15:21 |
 Sziasztok! Kissé most témát váltok, mert ezzel az érdekes feladattal futottam össze: A következő 6 valós számról tudjuk, hogy x>=y>=z>=t>=u>=w>=0, x+y>=100, z+t+u+w>=100. Kérdés: max(x*x+y*y+z*z+t*t+u*u+w*w)=? Az x*x+y*y a legnagyobb akkor lenne, ha x=100 és y=0 ellenben ekkor 0=y>=z miatt a szóbanforgó négyzetösszeg lehet jóval nagyobb is. Ha az x értékét csökkentem, és y értékét növelem, akkor természetesen x*x+y*y csökken, de ha y értéket növelem, akkor a z,t,u,w értékeivel a négyzetösszeget jobban növelhetem (?) mint amennyire az x*x+y*y összeget csökkentettem. Az összeget sejtésem szerint úgy maximzálhatom, ha x=y=50 és z=t=50 és u=w=0. Ez a sejtésem, nem tudom igaz-e, és persze ez nem bizonyítás! Ide elkelne valami jó ötlet, mert amit leírtam nem bizonyítás, és talán nem is helyes?! Előre is kösz!
|
|
|
|
| [1769] psbalint | 2007-01-17 13:43:02 |
 Az állítás nem vonatkozik azokra a kártyákra, amiken az 1-est és a 3-ast látjuk, ezek tehát nem érdekelnek minket. A másik kettőt viszont mindenképpen meg kell fordítanunk.
|
| Előzmény: [1768] Roberto85, 2007-01-17 13:07:10 |
|
| [1768] Roberto85 | 2007-01-17 13:07:10 |
 2. feladat Az alábbi négy kártyát látjuk, [1] [2] [3] [4] Mindegyik kártya mindkét oldalán 1-1 számjegy áll az 1-2-3-4 közül. LEgkevesebb hány kártyát kell megfordítani h eldöntsük: igaz e mind1ik kártyáára a következő állítás: Ha a kártya egyik oldalán 2es áll akkor a másik oldalán 4es?
|
|
| [1767] Roberto85 | 2007-01-17 13:04:11 |
 1feladat a, Van egymás mellett 5 ház, mind az 5 különböző színű b, A házakban egy egy személy lakik, mind különböző nemzetiségű c, MIndegyik fogyaszt valamilyen italt, dohányárút és tart valamilyen álatot. d, Egyikük sem fgyaszt ugyanolyan italt, szív ugyanolyan cigit, és tart ugyanolyan állatot.
Egyéb információk: 1. Brit piros házban lakik 2, svéd kutyát tart. 3. Dán teát iszik 4. fehér ház balján a zld ház van. 5, a zöld házban kávét fogyasztanak. 6. Az a személy aki Pall mallt szív, madarakat tart. 7. sárga ház lakója Dunhillt szív 8. Középső házban lakó tejet iszik 9. norvég az első házban lakik. 10.a Blendet szívó szomszédjában lakó macskát tart. 11. A blue mastert szívó ember sörözik 12.A lovakat tartó szomszédjábanlakó Dunhillt szív. 13. A német Prince-t szív 14. A norvég a kék ház szomszédja 15A blendet szívó ember szomszédjban vizet isznak
|
|
| [1766] Sirpi | 2007-01-17 07:56:06 |
 Ha jól értem, mivel kötött a menetrend, ezért tesszük fel, hogy az [a,b] intervallum fix. Viszont akkor az egyszerűség kedvéért legyen [a,b]=[0,1], a két város távolsága s, a vonat maximális gyorsulása pedig L (tehát [0,1]-en |f'(x)| L). L).
Nézzük meg, hogy maximálisan mekkora utat tud a vonat megtenni az adott idő alatt. Nyilvánvalóan az a legjobb stratégia, ha azonnal maximális gyorsításra kapcsol félútig, majd onnan maximális lassulásba kezd az út végéig. Az ehhez tartozó sebességgrafikon egy olyan egyenlő szárú háromszög két szára lesz, aminek a magassága L/2. És azért nyilvánvaló, hogy az ehhez tartozó út a maximális, mert az alatta lévő terület adja meg a megtett utat, és az összes többi stratégia grafikonja bele kell, hogy essen ebbe az egyenlő szárú háromszögbe.
A háromszög területe L/4, így rögtön adódik feltételként, hogy L 4s kell ahhoz, hogy a feladat megoldható legyen. 4s kell ahhoz, hogy a feladat megoldható legyen.
* * *
Most toljunk a háromszög felső csúcsától kezdve lefelé egy vízszintes egyenest. Ez elmetszi a két szárat, és a felső kis háromszöget figyelmen kívül hagyva egy egyenlő szárú trapézt kapunk a víszintes egyenes minden helyzete esetén. Állítsuk be úgy a felső egyenest, hogy a trapéz területe éppen s legyen. Megintcsak könnyen látható, hogy ez az optimális stratégia ahhoz, hogy a vonat maximális sebessége minimális legyen. Ugyanis tegyük fel, hogy van egy ennél is jobb. Ekkor ennek grafikonja végig a konstruált trapéz alatt kell, hogy haladjon - egyenlőség persze megengedett (a szárak fölé nem tud menni, mert akkor L-nél jobban gyorsulna, a felső vízszintes szakasz fölé megintcsak, mert akkor a maximális sebessége lenne nagyobb, mint a konstruált esetben). Viszont ekkor a görbe alatti terület kisebb kell legyen, mint a trapézé, vagyis a vonat nem éri el a célállomást, ami ellentmondás.
A max. sebesség minimuma könnyen ki is számolható: tegyük fel, hogy a vonat x idő után kezd állandó sebességgel haladni (és ekkor nyilván 1-x-nél kezd lassítani). A megtett út ilyenkor: L/4-(1-2x)2.L/4=s, vagyis 4x-4x2=4s/L, tehát x2-x+s/L=0. Innen
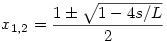
Ebből a kisebbre van szükségünk, a nagyobbik pont azt adja meg, hogy mikor kell lassítanunk.
* * *
A másik eset az, amikor a maximális sebesség maximalizálására törekszünk. Ekkor vegyük azt a stratégiát, amikor 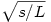 ideig maximálisan gyorsítunk, majd ugyanennyi idő alatt megállunk. ideig maximálisan gyorsítunk, majd ugyanennyi idő alatt megállunk. 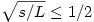 a feltételek szerint, tehát ez egy megvalósítható stratégia. Ilyenkor a megtett út a feltételek szerint, tehát ez egy megvalósítható stratégia. Ilyenkor a megtett út 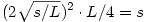 . Minden más stratégia viszont, aminél a maximális sebesség nagyobb, mint jelen esetben, szükségképpen több utat jelent, hiszen ha a(z egyik) maximális sebességű pontból L és -L meredekségű félegyeneseket húzunk lefelé, akkor az teljes egészében az eredeti út görbéje alatt kell hogy elhelyezkedjen a maximális gyorsulás miatt, és a félegyenesek által kifeszített háromszög is nagyobb területű lesz, mint s (a háromszög nagyobb magassága miatt), ami ellentmondás. Vagyis megkaptuk a maximális sebesség maximumát is. . Minden más stratégia viszont, aminél a maximális sebesség nagyobb, mint jelen esetben, szükségképpen több utat jelent, hiszen ha a(z egyik) maximális sebességű pontból L és -L meredekségű félegyeneseket húzunk lefelé, akkor az teljes egészében az eredeti út görbéje alatt kell hogy elhelyezkedjen a maximális gyorsulás miatt, és a félegyenesek által kifeszített háromszög is nagyobb területű lesz, mint s (a háromszög nagyobb magassága miatt), ami ellentmondás. Vagyis megkaptuk a maximális sebesség maximumát is.
Ha gond lenne az, hogy a vonat előbb ér az állomásra, mint kellene neki, akkor megtehetjük, hogy a konstruált háromszög területét nagyon picit csökkentjük, és a lassítási ág legvégén nagyon lassan gurulva tesszük meg az út utolsó 1 cm-ét (de ez már csak finomkodás).
* * *
Végeredmény:
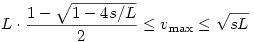
|
| Előzmény: [1764] Lóczi Lajos, 2007-01-17 01:52:30 |
|
| [1765] Lóczi Lajos | 2007-01-17 02:34:28 |
 Kicsit pontosabban megfogalmazva, a kérdést úgy akarom feltenni tehát, hogy mi lehet a maximális sebesség minimuma, illetve maximuma a megengedett sebességfüggvények halmazán. Tehát ez egy feltételes minimax és "maximax" feladat.
|
| Előzmény: [1764] Lóczi Lajos, 2007-01-17 01:52:30 |
|
| [1764] Lóczi Lajos | 2007-01-17 01:52:30 |
 Egy utazásom alkalmával jutott eszembe ez a teljesen gyakorlati kérdés -- számomra nagyon nehéznek tűnik, leginkább variációszámítás-ízű. Ezért nyugodtan tegyünk mindenféle egyszerűsítő feltevéseket, hogy bármiféle eredményt kapjunk. Tehát:
Adott két város, köztük egyenes vonalú pályán egy vonat fut. A két végállomáson a vonat sebessége persze nulla, menet közben a gyorsulás és lassulás természetesen korlátozott. A két város távolsága adott, a távolság megtételéhez szükséges idő szintúgy. A kérdés az, hogy mi lehet a vonat maximális sebessége, illetve ennek alsó/felső becslése.
Vegyünk fel adatokat tetszés szerint, hogy érdekes feladatokat kapjunk, mindenféle részeredményre kíváncsi vagyok.
Egy lehetséges modell a következő: adott egy f:[a,b] R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n. R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
|
|
| [1763] rizsesz | 2007-01-16 23:03:25 |
 Szóval nekem az lenne a kérdésem Roberto, hogy ezek a feladatok mihez segítenek hozzá, mármint ha megoldod őket, és beadod? Ismered azt, akinek odaadod?
|
|
| [1762] rizsesz | 2007-01-16 22:59:41 |
 Azért ha az egyenlet-rendezés nem megy, az azért elég aggasztó, nem? Mármint így mi értelme van a feladatok megoldását megadni?(moderáljatok engem!).
|
|
| [1761] Lacczyka | 2007-01-16 22:08:03 |
 Szerintem olvasd át S. Ákos [1737]-ben leírt megoldását. Ebben a végén kijönnek az oldalak, és ebből már nem gond sem a felszín, sem a térfogat kiszámítása. A másik megoldás (az csak a felszínre volt) a Te szempontodból nem lényeges. Viszont ha valamit nem értessz ebből a megoldásból [1737], akkor kérdezz rá konkrétan, sorra pontosan.
Lacczyka
|
| Előzmény: [1760] Roberto85, 2007-01-16 19:27:31 |
|
|
| [1759] Roberto85 | 2007-01-16 17:17:48 |
 még lenne egy kérdés, h amikor ki kell vonni az a2+b2+ab=84et, máskor meg hozzáadni, na ez miért kell?
|
|
| [1758] Csimby | 2007-01-16 16:59:09 |
 Nézheted fentről le is, no: c(a2-c2)=b(a2-b2) - ezt akarjuk bizonyítani. Most a2 - helyére beírjuk b2+bc+c2-t mindkét oldalon, (koszinusz tételből tudjuk hogy ezt megtehetjük) így ezt kapjuk: c(b2+bc+c2-c2)=b(b2+bc+c2-b2) Itt most egyszerűsítesz a zárójeleken belül, marad: c(b2+bc)=b(bc+c2) Kiemelsz baloldalból b-t, jobb oldalból c-t és ami marad: bc(b+c)=bc(b+c) Ami pedig nyilván igaz, így a bizonyítandó állítás is igaz volt, hiszen végig ekvivalens átalakításokat végeztünk.
|
| Előzmény: [1738] S.Ákos, 2007-01-13 19:23:33 |
|
| [1757] Roberto85 | 2007-01-16 16:44:24 |
 hát nézem visszafele, dehát nemértem ezt azért tényleg jó lenne ha elmagyaráznátok mindent lépésről lépésre...
|
|
|
| [1755] Csimby | 2007-01-16 16:25:42 |
 [1738]-nél alulról indulj ki és úgy következnek egymás utána a lépések felfelé, míg végül megkapjuk a bizonyítandó állítást. Utolsó lépésben felhasználjuk a2=b2+bc+c2-et is.
|
| Előzmény: [1753] Roberto85, 2007-01-16 15:55:26 |
|
|
| [1753] Roberto85 | 2007-01-16 15:55:26 |
 Felírva a koszinusz-tételt az a oldalra kapjuk, hogy
a2=b2+bc+c2 és ezutánni részt nem értem h jön ide, hogy c(a2-c2)=b(a2-b2) meg hogy ezután még ebből hogy lesz c(b2+bc+c2-c2)=b(b2+bc+c2-b2) azet a két lépést mondjátok el, azután nem zaklatlak benneteket :)
|
|
|
| [1751] Roberto85 | 2007-01-16 14:09:14 |
 amúgy vannak még feladataim :) 1. Egy gömb felületén véletlenszerűen választunk 3 pontot, mennyi a valószínűsége, h a választott pontok egy félgömbön lesznek?
2. Létezhet e olyan test, melynek oldalnézete négyzet, elölnézete háromszög, felülnézete kör :)
3. Körülbelül hány tonna követ használtak fel a Kheposz piramis építői (a mészkő sűrűsége 2,7 tonna köbméterenként) Kheposz fáraó 23 évig uralkodott. Hány köbméter követ kellett megmozgatniuk naponta, ha feltételezzük h 23évig épült? csak ennyi van megadva :S
|
|
|
|
| [1748] Roberto85 | 2007-01-16 12:26:35 |
 de pl a cosinus és sinusos fealdatnál amikor 4 az alapja. na szval annak a végén a megoldásnak van bent valami k betű az ott mi lenne? mert nekem a kerület ugrik be így elsőre...
|
|
| [1747] Roberto85 | 2007-01-15 19:29:07 |
 tenném én fel, de hát nem látom gybe a feladatokat...
|
|
| [1746] Sirpi | 2007-01-15 18:41:15 |
 Na, végre egy konkrét kérdés :-)
A koszinusz-tétel szerint minden háromszögben a2=b2+c2-2bccos  . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-) . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)
|
| Előzmény: [1745] Roberto85, 2007-01-15 17:25:22 |
|
| [1745] Roberto85 | 2007-01-15 17:25:22 |
 meg hát főleg az lenne a kérdés h amikor bizsonyítani kell a 3szögesnél hova lett a 120fok?
|
|
|
|
| [1742] Roberto85 | 2007-01-14 19:41:10 |
 Látom én h szépen kiszámoltátok őket, nagyon köszönöm is... csak hát kicsit kuszán vannak a feladatok...
de pl ezt a szinuszosat meg a 3szögeset fullra nem értem... szval én már a kezdésnél csak lesek, azt se tudom h melyik feladat hol kezdődik :( pedig nem vagyok segg hülye matekból csak hát nekem ezek már nehéz feladatok amúgy tényleg nagyon köszi
|
|
| [1741] Sirpi | 2007-01-14 17:56:02 |
 Szerintem játsszuk azt, hogy írd le, hogy Te melyik lépéseket nem érted, és azt majd elmagyarázzuk. De miután ilyen szépen ki lett fejtve minden feladat megoldása, tényleg nem baj, ha egy kicsit Te is dolgozol :-) Szóval várjuk a konkrét kérdéseidet.
|
| Előzmény: [1740] Roberto85, 2007-01-14 17:10:34 |
|
| [1740] Roberto85 | 2007-01-14 17:10:34 |
 bocsi de tényleg nem értem, mert elég összevissza vannak a feladatok... és ha valamit rosszul írok le akkor levágják h nem én csináltam! Meg amúgy is bele szokott kérezni, szval nagyon megköszönném ha írnál mellé egy kis magyarázó szöveget
|
|
| [1739] Roberto85 | 2007-01-13 21:45:48 |
 húúúha nekem itt nagyon összekeveredtek a dolgok h melyik melyik feladat :D megtudnád tenni h mind a 3 feladatot leírod egyszerre? :D
és a sin-os cos-os, és ezt a 3szögeset elmagyaráznád? mert ha belekérdez elég hülyén veszi ki magát h nem tudom :)
eddigiekért is nagyon köszi :)
|
|
|
| [1737] S.Ákos | 2007-01-13 19:16:02 |
 2. A térfogat:
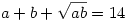
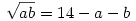
ab=196+a2+b2-28(a+b)+2ab
-ab=196+a2+b2-28(a+b)
ezt (1)-hez adva:
a2+b2=280+a2+b2-28(a+b)
a+b=10
innét 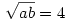
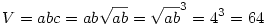
(a téglaest élei 2,4,8 egységnyiek, ezt az ab=16 a+b=10 egyenletrendszer megoldásával nyerhetjük)
|
| Előzmény: [1735] S.Ákos, 2007-01-13 14:12:07 |
|
|
| [1735] S.Ákos | 2007-01-13 14:12:07 |
 Ennyire jutottam eddig:
1. L melyik oldallal szembeni szöget jelöli?
2. Legyenek a téglatest élei a, b, c, és legyen 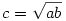 ! Ekkor felírható: ! Ekkor felírható:
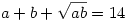
vagyis
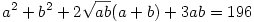
ebből kivonva (1)-et
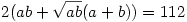
-Ennyi a téglatest felszíne.
3. Ismeretes, hogy cos2x+sin2x=1, így az egyenlet sin2x=y helyettesítéssel 4y+41-y=4alakba írható, innét: 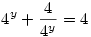 . Most legyen 4y=z, így az egyenlet . Most legyen 4y=z, így az egyenlet
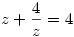
alakot ölt. Ennek megoldása az z=2, így
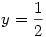
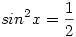
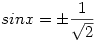
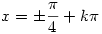
|
| Előzmény: [1734] Roberto85, 2007-01-13 11:06:32 |
|
| [1734] Roberto85 | 2007-01-13 11:06:32 |
 hello kaptam pár feladatot matekórán ha segítenétek megoldani őket nagyon megköszönném. Előre is köszi /sűrgős lenne/
Bizonyítsd be, hogy ha egy háromszögben L= 120 fok, akkor c(a2-c2)=b(a2-b2)
Egy téglatest egy csúcsból kiinduló éleinek összege 14, négyzetük összege 84. Egyik él mértani közepe a másik kettőnek. Mekkora a téglatest felszíne és térfogata?
|
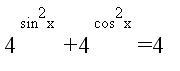 |
|
| [1733] Cckek | 2007-01-13 00:52:24 |
 Áltlánosítok mert két számra megoldottam. Tehát azt a legkissebb k-t keressük, hogy mindig kiválasztható legyen közüle p szám,(p adott) úgy hogy ezek közé elhelyezhetőek legyenek a + illetve - műveletek úgy hogy az eredmény osztható legyen n-nel.
|
| Előzmény: [1732] Cckek, 2007-01-13 00:07:19 |
|
| [1732] Cckek | 2007-01-13 00:07:19 |
 Nos jó... Akkor egy kis matematika. Ismert dolog, hogy 5 természetes szám közül mindig kiválasztható 2 úgy, hogy a különbségük, vagy összegük osztható legyen 7-tel. Akkor általánosítsuk ezt. Adott n esetén, határozzuk meg azt a k-t, hogy k szám közül mindig kiválasztható legyen 2 melynek a különbsége vagy összege osztható legyen n-el. Pl n=9-re k=6. Ez nagyon érdekes, mert k nyilván függ n-től, de kérdés hogy megadható-e zárt formában?
|
|
| [1731] rizsesz | 2007-01-12 19:09:42 |
 Nem tudom, hogy miért baj az, ha valaki felnéz valakire, és miért kell ezt nyalizásnak minősíteni. Attól még, hogy itt egyenlő félként, mindenki matematikával foglalkozik, még megadhatjuk egymásnak azt a jogot, hogy emberként viselkedünk egymással, és ha valaki segít nekünk, és veszi a fáradtságot, és pl. javaslatot tesz valamire, vagy neadjisten, még azt is megmondja, hogy hogyan kell valamit TeXben megírni, akkor azt nem kioktatásnak vesszük. Már ha ez lehetséges.
|
| Előzmény: [1730] Cckek, 2007-01-12 16:59:57 |
|
| [1730] Cckek | 2007-01-12 16:59:57 |
 Ugyan nem fogom már a topic témáját megváltoztatni, de azt már hadd döntsem én le, hogy kire nézek fel:)). Amúgy privátba nyalizz ez a topic itt a matematikáról szól, vagy legalábbis azt hittem eddig.
|
| Előzmény: [1728] nooby, 2007-01-12 14:25:42 |
|
| [1729] HoA | 2007-01-12 16:15:36 |
 Akkor konkrétan:
Állítás: Ha 2x-1 osztója 2p-1 -nek, akkor x megfelel.
Ebből az is következik, hogy
a) a legkisebb x>1 -et a legkisebb 2x-1 > 1 alakú osztóból kapjuk - és mind ilyen alakú.
b) Minden p-hez van x - ha kisebb nem, akkor p maga.
Bizonyítandó az Állítás és esetleg a fordítottja is.
|
| Előzmény: [1728] nooby, 2007-01-12 14:25:42 |
|
| [1728] nooby | 2007-01-12 14:25:42 |
 Cckek: Szerintem Sirpi nem kiosztani akart, csak jelezte, hogy szebben is beírhatnám a feladatot. Véleményem szerintem jogos volt. Egyébként meg mindkettőnknek van oka felnézni Rá ;) (Nézd meg az infot Róla, ha másképp vélekedsz!)
HoA: Ezt a 2p-1 osztóit kereső megoldást én is megtaláltam, azért tettem fel a kérdést, mert reméltem, hogy Ti tudtok rá valami mást mondani. Egyébként gratulálok!
U.i.: Sirpit már csak azért is meg kell védenem, mert én is majdnem ott fogok (remélhetőleg) diplomát szerezni, ahol Ő :)
|
| Előzmény: [1725] Cckek, 2007-01-12 13:12:23 |
|
| [1726] Sirpi | 2007-01-12 13:28:54 |
 Bocs, ha kioktatásnak érezted, igazából csak azért írtam le, hátha többen látják, hogy nem ördöngösség ez, és bátran lehet használni. Szebb is lesz a végeredmény, meg az illető is nagyobb lelki nyugalommal posztolhat tudván, hogy nem értik félre.
Bocs, ha kioktatónak tűntem, nem fogok ilyen hsz-t gyakran hegeszteni...
|
| Előzmény: [1725] Cckek, 2007-01-12 13:12:23 |
|
| [1725] Cckek | 2007-01-12 13:12:23 |
 Még jó, hogy ez a forum arról szól, hogy a matematikában érdekeltek, egyenrangú félként megbeszéljenek, megvitassanak dolgokat, esetleg segítsenek egymásnak bizonyos problémák megoldásában, és nem arról, hogy hogyan kell mindenkit kioktatni!:))
|
| Előzmény: [1727] Sirpi, 2007-01-12 10:53:42 |
|
| [1727] Sirpi | 2007-01-12 10:53:42 |
 Ajánlom figyelmedbe (és mindenki más figyelmébe is) a fórumhoz készített TeX-tanfolyamot-ot.
a b: $a \neq b$ b: $a \neq b$
a b: $a \equiv b$ b: $a \equiv b$
És amit még furán szoktak használni (*-gal):
a.b: $a \cdot b$
Szerintem nagyon hamar bele lehet szokni a dologba. Szóval az eredeti feltétel így néz ki TeX-ben:
p 2x2mod 4x-2, x 2x2mod 4x-2, x 1 1
$p \equiv 2x^2 \mod 4x-2$, $x \neq 1$
|
| Előzmény: [1721] nooby, 2007-01-11 18:25:31 |
|
| [1724] HoA | 2007-01-12 09:00:02 |
 Azt hiszem megvan a megoldás. Nem akarom ellőni, ezért egyelőre csak ennyit : Keressetek öszefüggést 2p-1 legkisebb valódi osztója és a p-hez található legkisebb x > 1 között.
|
| Előzmény: [1723] nooby, 2007-01-11 20:57:44 |
|
| [1723] nooby | 2007-01-11 20:57:44 |
 Nézzük a p=8 esetet. Ekkor szerintem az x=2 a legkisebb, mivel: 8 kongruens 8 (mod 4*2-2), de ha kipróbáltok más p-ket, akkor látszik, hogy változó, hogy mi lesz az optimális x értéke. Ha gondoljátok írhatok még néhány (p, x) párt...
|
| Előzmény: [1722] jenei.attila, 2007-01-11 20:37:24 |
|
|
| [1721] nooby | 2007-01-11 18:25:31 |
 Nos, jutott valaki tovább esetleg? Egyébként az, hogy valaki nem vette észre, hogy az egyet nem tekinti a feladat megoldásnak, az valószínű az én hibám, mert én nem tudok ilyen matematikai kifejezéseket írni, mint nemegyenlő, kongruens... ezért inkább máshogy próbálom ezeket olvasható formába önteni.
Különben a feladat megoldásának nem muszáj egy zárt képletnek lennie. Elég az, ha egy (asszimptotikusan) jobb algoritmust mond valaki ennél: for(int i=2; (...); i++) . Remélem, sokat segítettem ;)
|
| Előzmény: [1720] HoA, 2007-01-11 17:16:36 |
|
|
|
|
|
| [1716] nooby | 2007-01-11 15:10:48 |
 Sziasztok!
Remélem, hogy tud valaki segíteni a következő feladat megoldásában, mert nekem nem sikerül:
Adott az alábbi kongruencia:
p kongruens 2*x*x mod 4x-2
Ahol p egy természetes szám, paraméter. A feladat az lenne, hogy keressük a legkisebb olyan x természetes számot (x<>1) , amire az alábbi kongruencia teljesül.
Nekem a brute-force-nál gyorsabb módszer kéne, vagyis, hogy ne kelljen végignézni 2től a számokra, hanem valahogy gyorsabban meg lehessen határozni.
Előre is köszönöm, és aki megmondja, azt hálám a sírig fogja üldözni.
|
|
| [1715] psbalint | 2007-01-10 21:45:14 |
 köszönöm szépen a segítséget a feladattal kapcsolatban
|
|
| [1714] Pirigyi Roland | 2007-01-10 17:31:24 |
 Kössz Sirpi én nem akartam senkit beugratni , hanem engem ugrattak be asszem :))) köszi
|
|
| [1713] Sirpi | 2007-01-10 17:18:08 |
 Remélem, nem az a beugratás, hogy n a futó index, f pedig x-től függ :-) (ilyenkor ugyanis f(x) konstans, és igaz az állítás).
Amúgy meg nem igaz, legyen pl. f(x)=1, ha x racionális, különben pedig f(x)=-1. Ilyenkor minden a-ra van |f(x)|-nek határértéke (és =1), viszont f(x)-nek semmilyen a-ra nincs.
|
| Előzmény: [1712] Pirigyi Roland, 2007-01-10 14:23:03 |
|
| [1712] Pirigyi Roland | 2007-01-10 14:23:03 |
 Döntse már el nekem valaki , hoyg ez igaz vagy hamis :) elöre is köszönöm. Roland
Ha létezik 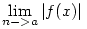 ,akkor létezik ,akkor létezik 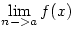 is. is.
|
|
| [1711] jonas | 2007-01-10 12:09:55 |
 Szerintem még csak integrál sem kell bele. Két körszelet területét kell összeadni, ezekre meg van egyszerű képlet. Viszont persze a kifejezés lehet annyira szögfüggvényes, hogy ha a feladathoz felírjuk az egyenletet, akkor azt nem tudjuk zárt alakban felírni.
|
| Előzmény: [1709] Cckek, 2007-01-09 18:25:30 |
|
|
| [1709] Cckek | 2007-01-09 18:25:30 |
 Elnézést a közbeszólásért de k értéke kiszámítható r függvényében ugyanis a lelegelendő terület felírható integrálok különbségeként. Nos a számítások bonyolultak én pedig lusta vagyok, de úgy nézem hogy a képletben mindenképpen szerepel az arcsin függvény bizonyos értéke. Talán innen ered a megtszerkeszthetetlenség.
|
| Előzmény: [1707] HoA, 2007-01-09 17:18:16 |
|
| [1708] psbalint | 2007-01-09 17:38:50 |
 Igazság szerint én megpróbáltam kifejezni a kötél hosszának értékét r-rel. Ha nem lehet egy zárt formulát adni, akkor viszont örülnék ezen állítás bizonyításának.
|
|
| [1707] HoA | 2007-01-09 17:18:16 |
 Nincsenek régi viccek, csak öreg emberek... A feladatot szerintem a Fórumosok ismerik, ami nem baj, mert itt inkább az az érdekes, mit jelent az, hogy "nem boldogulok vele". Nyilván látod, hogy mivel minden kör hasonló egymáshoz, a megoldás k*r, ahol 1 < k < 2 , hiszen az r hosszú kötéllel a terület felénél kevesebb legelhető le, 2r -nyi kötéllel pedig az egész kert. k numerikus értéke fokozatos közelítésekkel (számítógépes programmal, kézi számolással) tetszőleges pontossággal kiszámítható. Könnyen belátható, hogy a legelhető terület k-nak monoton függvénye, így adott k-hoz kiszámítva a legelhető területet, attól függően, hogy az nagyobb vagy kisebb a fél kertnél, k-t csökkenteni vagy növelni kell, míg el nem érjük a kitűzött pontosságot. De ha azt várjuk, hogy k-t valamilyen zárt alakban felírhassuk, például "szerkeszthető" lenne, tehát egész számok, a négy alapművelet és négyzetgyökök használatával felírható, akkor csalódnunk kell. A Fórum olvasói számára talán éppen ez lehet egy jó kis feladat: Bizonyítsuk be, hogy k nem szerkeszthető.
|
| Előzmény: [1706] psbalint, 2007-01-09 15:38:27 |
|
| [1706] psbalint | 2007-01-09 15:38:27 |
 Üdvözlök mindenkit! Egy feladatot szeretnék elmondani, remélem még nem volt, ha volt, elnézést. Nagyon egyszerűnek tűnik mégsem boldogulok vele...
Egy kör alakú kert sugara r, a körvonal egy pontjához belülről hozzákötünk egy kecskét egy kötéllel. Milyen hosszú legyen a kötél, hogy a kecske a kör területének felét tudja lelegelni?
|
|
|
|
| [1703] Cckek | 2007-01-08 22:22:19 |
 Ugyan már máshol is kitűztem, de nem érkezett megoldás rá, remélem itt együttesen megoldjuk: Oldjuk meg a következő funkcionálegyenletet
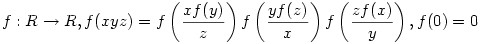 . .
|
|
| [1702] magusocska | 2007-01-08 19:33:53 |
 Egy QBASIC program 2.5 mp alatt kihozta, hogy 48 megoldás van.
A progi lényegében kipróbálta az oszhatósági szabályokat a fokozatosan növelt helyiértékszámú számokra.
Más, "elegánsabb" módszer nem lenne?
|
| Előzmény: [1697] magusocska, 2007-01-08 08:03:44 |
|
| [1701] bgy67 | 2007-01-08 17:49:27 |
 A következő problémám lenne, segítsen, aki tud!
12k+4 embert akarok 4-személyes asztalokhoz leültetni (römi-verseny) 4k+1 fordulóban úgy, hogy mindenki mindenkivel pontosan egyszer játsszon.
Egy órát kerestem google-val, de nem találtam táblázatot, csak azt a tételt, hogy ez mindig megoldható.
16 személyre meg is csináltam, egyszerűen mindig a legkisebb lehetséges sorszámú személyt ültettem le sorban és kijött, lehet hogy ez mindig működne, de programozni annyira nem tudok, hogy megcsináljam, kézzel meg hosszú. "Szép" mintát meg nem találtam, amit általánosítani lehetne.
Aki találkozott a problémával (gráfelmélet, véges testek??), és tud sorsolást leglább 28 és 40 főre, pls szóljon.
|
|
| [1700] magusocska | 2007-01-08 09:52:47 |
 Teljesen igazad van - elnézést kérek [ vadidegenül szorri :-)) ]
Csak magyarázatképpen említem meg, hogy
- túlságosan hozzá vagyok (gyunk) szokva az intelligens ellenőrzőrendszerekhez (nincs aláhúzás? akkor mehet)
- egy sort írtam le, a többi másoltam, és csak a számokat javítottam át, a toldalékokat nem
- a gyors kommunikációs kényszer (sms, email,chat) miatt egyre kevesebb jelentőséget tulajdonítunk (és sajnos ezek szerint -tok) a helyesírási konvencióknak
- és Proszékyék még nem publikálták a KÖMAL fórumra is alkalmazható ellenőrző rutincsomagjukat :-)
|
| Előzmény: [1699] BohnerGéza, 2007-01-08 09:02:58 |
|
| [1699] BohnerGéza | 2007-01-08 09:02:58 |
 Nagyon örvendetes, ha valaki tisztában van idegen szavak jelentésével. ( politikai publicitás, korifeus, kontextus, konvenció )
De jó lett volna az alapvető magyar szabályokat is betartani az előző hozzászólásban! ( Teljes hasonulás. )
kilenccel 9-cel nyolccal 8-cal ...
a legcsúnyább a 2-el, a 2-vel helyett!
Sajnos rengeteg helyen látni rosszul írva ezeket a sajtóban!
|
| Előzmény: [1698] magusocska, 2007-01-08 08:20:32 |
|
| [1698] magusocska | 2007-01-08 08:20:32 |
 Érdekes is, matematika is, de kérdés, hogy feladat-e, mindenesetre túl vagyok rajta.
Peano politikai publicitásáról hallottatok-e? (Összerugtam a port a lányom matektanárjával - így derült ki az ellentmondás.)
A természetes számok Peano féle meghatározása tartalmazta a nullát, az én egyetemi jegyzeteimben a természetes számok pozitív egészként szerepeltek, ma ismét az eredeti halmaz a hivatalos. A Lomonoszov korifeusaival lehet kapcsolatban az ügylet...
Tehát a kérdés (feladat): a magyar matematikaoktatásban mely években tanították a természetes számok halmazát az eredeti Peano-axiómától eltérően?
Megjegyzés:
A Wikipédia a következőt írja a "Természetes számok"-nál :
Vigyázat! Tekintve, hogy egyes matematikai tárgyú könyvek a természetes számok közé sorolják a nullát, mások nem, így minden esetben figyelmet kell fordítanunk arra, hogy utánanézzünk, az adott kontextusban a szerzők melyik konvenciót alkalmazzák.
|
|
| [1697] magusocska | 2007-01-08 08:03:44 |
 Mellyek az a 9 jegyű számok, amire igazak az alábbiak:
a 9 jegyű szám osztható 9-el,
ha elhagyjuk az utolsó jegyét, akkor az így kapott 8 jegyű szám osztható 8-al,
ha elhagyjuk az utolsó jegyét, akkor az így kapott 7 jegyű szám osztható 7-el,
. . .
ha elhagyjuk az utolsó jegyét, akkor az így kapott 2 jegyű szám osztható 2-el.
Elég könnyű legalább egyet találni (pl. 13694729) a jegyenkénti szabályalkalmazással, de az összes megtalálására a brutal force-n kívül van -e módszer?
|
|
|
| [1695] Sirpi | 2007-01-07 07:11:10 |
 Igaz, hogy már elhangzott egy sokkal frappánsabb megoldás (grat érte), de azért ha már kérdés, válaszolok:
Mivel |bn/2-bn+1|< minden n>N-re a folytonosság miatt, ezért bn/2- minden n>N-re a folytonosság miatt, ezért bn/2-  bn+1 bn+1 bn/2+ bn/2+ . Vagyis ha bn . Vagyis ha bn 3 3 , akkor (3/2-1) , akkor (3/2-1)  bn+1, tehát nem válthat előjelet (a bal oldali egyenlőtlenséget felhasználva), másrészt bn+1 bn+1, tehát nem válthat előjelet (a bal oldali egyenlőtlenséget felhasználva), másrészt bn+1 bn/2+ bn/2+  bn/2+bn/3 bn/2+bn/3 bn, tehát a sorozat monoton is. bn, tehát a sorozat monoton is.
Azt hittem, hogy ezek teljesen nyilvánvalónak látszanak az egyenlőtlenségből, azért nem részleteztem a dolgot ennyire.
Ha bn<0, akkor ugyanez elmondható, csak akkor a sorozat alulról, szintén monoton módon megy be a [-3 ;3 ;3 ] intervallumba. ] intervallumba.
|
| Előzmény: [1693] Lóczi Lajos, 2007-01-07 02:55:59 |
|
| [1694] Lóczi Lajos | 2007-01-07 03:23:19 |
 Köszönöm a megoldásokat, az állítás igazsága viszont azt jelenti, hogy most van egy sokkal kevesebb számolást igénylő megoldásunk az [1681]-es hozzászólás feladatára, az ugyanis alig igényel számolást belátni, hogy
un=2n-4/3+an
alakú, ahol an+2an+1 nullához tart és korlátos, tehát most már valóban tudjuk, hogy maga an is nullához tart, ez pedig elég ahhoz, hogy a -19/12-et kihozzuk.
|
| Előzmény: [1692] nadorp, 2007-01-07 00:32:48 |
|
| [1693] Lóczi Lajos | 2007-01-07 02:55:59 |
 Nyilván azzal kell kezdeni a bizonyítást, hogy a b sorozat bemegy a [-3 ,3 ,3 ] intervallumba. ] intervallumba.
"Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni." felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2-nál nagyobb értékhez nem tud konvergálni."
De ha nem menne be, miért maradna 3 felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat? felett? Miért ne ugrálhatna (pozitív és negatív értékekre) és főleg, miért kellene, hogy monoton legyen a b sorozat?
|
| Előzmény: [1688] Sirpi, 2007-01-04 23:47:54 |
|
|
| [1691] nadorp | 2007-01-06 12:56:32 |
 Legyen bn=an+2an+1. Ekkor
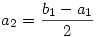
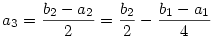
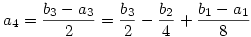
...
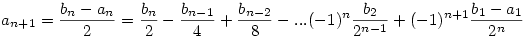 . .
Mivel 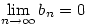 , ezért n>N esetén |bn|< , ezért n>N esetén |bn|< , azaz , azaz
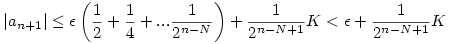 , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy , ahol K a |b1-a1|,|b2|,|b3|... egy közös felső korlátja. ( Ez létezik, mert bn konvergens). Innen már látszik, hogy 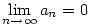
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
|
|
| [1688] Sirpi | 2007-01-04 23:47:54 |
 Igaznak tűnik :-)
Tegyük fel, hogy an nem azonosan 0 egy adott indextől kezdve, és teljesül rá a feltétel. Cseréljük ki an-et egy bn sorozatra úgy, hogy bn=an, ha n páros, és bn=-an, ha n páratlan. Ekkor a feltétel ekvivalens bn/2-bn+1 konvergenciájával (ezzel egyszerűbb talán dolgozni, mert nem "oszcillál").
Legyen  >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< >0. Ekkor a konvergencia miatt van olyan N, hogy minden n>N-re |bn/2-bn+1|< . .
Mivel bn nem azonosan nulla valamilyen indextől, ezért van olyan m>N, amire bm 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2- 0 (feltehetjük, hogy pozitív, különben a bn sorozat helyett vegyük az ellentettjét). Ekkor bm/2-  bm+1 bm+1 bm/2+ bm/2+ , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 , vagyis (és ez a lényeg) a sorozot bm-től kezdve előbb-utóbb bemegy a [-3 ;3 ;3 ] intervallumba, és onnan már nem is tud kijönni, így 3 ] intervallumba, és onnan már nem is tud kijönni, így 3 -hoz van megfelelő N' korlát. -hoz van megfelelő N' korlát.
Az, hogy ha bemegy, akkor nem tud kijönni, triviális, hiszen 0/2-  bn+1 bn+1 3/2 3/2 + + , azaz a következő elem abszolútértéke 5/2 , azaz a következő elem abszolútértéke 5/2 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 lesz maximum. Az pedig, hogy valóban be is megy, következik abból, hogy ha nem menne be, akkor végig 3 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 felett maradna, valamint monoton módon csökkenne (ezt is könnyű látni), tehát konvergens lenne, de 2 -nál nagyobb értékhez nem tud konvergálni. -nál nagyobb értékhez nem tud konvergálni.
Tudom, ez így kicsit kusza, meg hosszú volt, de már kezd késő lenni. Nem tudom, van-e sokkal egyszerűbb(en leírható) megoldás.
|
| Előzmény: [1687] Lóczi Lajos, 2007-01-04 22:25:16 |
|
| [1687] Lóczi Lajos | 2007-01-04 22:25:16 |
 Bizonyítsuk be vagy cáfoljuk meg az alábbi állítást:
"Ha an egy olyan korlátos valós számsorozat, amelyre an+2an+1 nullához tart, akkor an konvergens" (és ekkor persze maga is nullsorozat).
|
|
|
|
|
|
|
|
|
|
|
|
| [1675] Mumin | 2007-01-01 20:10:32 |
 Hány SET-kártyát lehet legfeljebb kirakni az asztalra, hogy ne kiálthasson senki Set!-et?
Aki egyszerűnek találja, ne lője le.
|
|
|
| [1673] S.Ákos | 2007-01-01 19:11:48 |
 Maradékvizsgálat nélkül: Mivel a 0001;0002;0004;0008;0016 végződések nem felelnek meg, így az utolsó négy számjegyből alkotott szám osztható 16-tal és 1111-gyel, de ezeknek a közös többszörösei 0;17776;... így csak a 0000 jöhet szóba, de ez lehetetlen.
|
| Előzmény: [1671] jonas, 2007-01-01 17:32:26 |
|
|
| [1671] jonas | 2007-01-01 17:32:26 |
 (a) 239=549755813888
(b) Ehhez elég a 2-hatványok 10000-es maradékát megvizsgálni. Ez persze ciklikus, hiszen 2504 24 24 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset): 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset):
0001 0002 0004 0008 0016 0032 0064 0128 0256 0512 1024 2048 4096 8192 6384 2768 5536 1072 2144 4288 8576 7152 4304 8608 7216 4432 8864 7728 ... 8752 7504 5008
Ezek között pedig nincs 1111-gyel osztható.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|
| [1669] Lóczi Lajos | 2007-01-01 17:21:13 |
 a.) Az első 1600 kitevő átvizsgálása az alábbi eredményt adja: 2n pontosan akkor végződik 3 egyforma számjegyre, ha n az alábbi:
n=39,139,239,339,439,.... Ekkor amúgy mindig 888-ra végződik 2n.
b.) A számítógép 85 másodperc gondolkodás után nem tudott olyan 2-hatványt mondani, ami 4 egyforma számjegyre végződne. Az átvizsgált n kitevők tartománya: n=1-től egészen n=107-ig.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|
|
| [1666] Python | 2007-01-01 15:29:09 |
 304. feladat
a)Végződhet-e egy kettőhatvány 3 egyforma számjegyre? (10-es számrendszer)
b)Végződhet-e egy kettőhatvány 4 egyforma számjegyre? (10-es számrendszer)
|
|
| [1665] Lóczi Lajos | 2006-12-31 14:00:09 |
 Számunkra már több, mint egy éve nyitott az alábbi ártatlannak tűnő kérdés: oldjuk meg a valós számok halmazán a
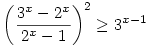
egyenlőtlenséget. Az eredményt persze tudjuk, csak a bizonyítást nem. Hátha valaki talál egy ügyes utat...
|
|
|
|
| [1662] Cckek | 2006-12-30 17:53:39 |
 Jólismert egyenlőtlenségek a G<L<A ahol
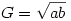 , ,
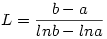 , ,
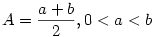 . .
Tud rájuk valaki egy egyszerű bizonyítást?
|
|
| [1661] HoA | 2006-12-29 16:40:53 |
 A képlet bizonyítása: Rakjunk le egy sorba s + n - 1 ( 222 + 4 - 1 = 225 ) fehér korongot. Közülük n-1 (3) tetszőlegeset takarjunk le egy-egy fekete koronggal. Minden ilyen lefedés a le nem takart s (222) korongot n (4) csoportra bontja, melyek közt 0 elemszámúak is lehetnek. Feleltessük meg, mondjuk balról jobbra az egyes csoportok elemszámát az ai (x,y,z,t) változóknak, ekkor egyenletünk egy megoldását kapjuk. Így kölcsönösen egyértelmű leképezést kapunk a lefedések és a megoldások között, tehát megoldás is ponosan annyi van, mint lefedés. Ezek száma pedig a képlet szerinti.
|
| Előzmény: [1660] Cckek, 2006-12-29 10:33:28 |
|
|
|
|
| [1657] Cckek | 2006-12-28 15:06:49 |
 Hány megoldása van a természetes számok halmazában az x+y+z+t=222 egyenletnek?
|
|
| [1656] HoA | 2006-12-27 13:24:26 |
 Mivel eddig senki sem szólt hozzá, leírok egy megoldást.
Racionáls a,b 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 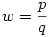 , , 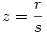 , ahol p,q,r,s egészek. , ahol p,q,r,s egészek. 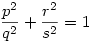 ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek. ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek.
p2u2n2+r2t2n2=t2u2n4 ; p2u2+r2t2=t2u2n2 A baloldalon t és u relatív prím volta miatt p2 osztható t2 -tel és r2 osztható u2 -tel. Legyen p=kt, r=mu. k2t2u2+m2u2t2=t2u2n2
k2+m2=n2
Vagyis tetszőleges k,m,n pithagoraszi számhármashoz kapunk megoldást. Visszafelé haladva tetszőleges relatív prím t-t és u-t véve 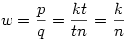 , , 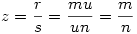 , , 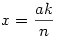 , , 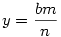
Az ellipszis racionális koordinátájú pontjai tehát a 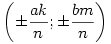 pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg. pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg.
|
| Előzmény: [1625] Cckek, 2006-12-15 14:58:40 |
|
|
|
| [1653] Hephon | 2006-12-25 16:17:19 |
 Minden üveg sorszáma elfér 10 számjegyen binárisan (<1024). Minden bináris helyiérték 1-1 halálraitélthez tartozik. Minden borral megitatja azokat az embereket, ahol ez a helyiérték 1, tehát az 1. borbol csak az első szolga, a 100. borbol(64+32+4) tehát a 3. 5. 6. halálraitéltek isznak. 30. nap után az összes halottbol kiszámítha, hogy melyik bor volt a mérgező.
|
| Előzmény: [1652] Cckek, 2006-12-25 15:55:58 |
|
| [1652] Cckek | 2006-12-25 15:55:58 |
 Kellemes ünnepeket mindenkinek. És... a következő kis feladatot: Egy császár 1000 üveg borából 1 mérgezett. A császár kiadja a nagyvezérnek a parancsot, 40 nap alatt állapítsa meg melyik üveg mérgezett. Ehez kap 10 halálraítéltet akikkel a borokat kostoltathatja. A méreg 30 nap mulva hat. Hogyan jár el a nagyvezér?
|
|
|
| [1650] Iván88 | 2006-12-21 20:34:16 |
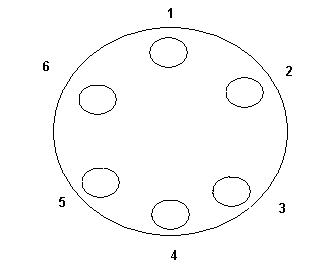
 Mivel a rendszer nem engedi feltölteni a 343 bájtos ábrámat (ami jóval a maximum alatt van) a kitöltetlen ábrádon fogok magyarázni. 4 különböző eset van a kézbedugásra:
3 szomszédos állásba (612)
2 szomszédos állásba, (124 ill. 614-ezek forgatással nyilván nem vihetők át egymásba)
0 szomszédos állásba (246)
Az össze további eset ezek közül valamelyiknek az elforgatottja.
A kapcsolók állása nyilván csak goldolatban van megszámozva, különben nem feladat. Ezzel a 4 félével, ha nincs szerencsénk, akkor kijöhet, hogy csak az 1246 kapcsolókhoz nyúlunk hozzá.
Tehát, ha a 3-as, és az 5-ös kapcsoló különböző állású, akkor elvileg az is előfordulhat, hogy sose nyúlunk hozzájun, és az ajtó is zárva maradhat az idők végezetéig.
Tehát áltaéános algoritmus nem létezik.
|
| Előzmény: [1649] magusocska, 2006-12-21 19:00:59 |
|
| [1649] magusocska | 2006-12-21 19:00:59 |
 Eddig jutottam:
Jelöljük a kapcsoló két állását 1-gyel és 2-vel!
Jelöljük a kapcsolókat 1-6, a felsőtől az óramutató járásával megegyezően.
[Ekkor az első kapcsoló jelölése legyen 1(1) vagy 1(2) attól függően, hogyan áll a kapcsoló 1 vagy 2 állásban, bizonytalan helyzetben 1 (1/2).]
Minden továbblépés előtt feltételezzük, hogy nem nyílik ki.
[Szerencsés esetben persze bármikor kinyílhat, akár induláskor is :*-) ]
1. Fogjunk meg három egymás melletti kapcsolót, és állítsuk mindhármat 2-re, ha nem az volt! [1(2),2(2),3(2) kapcsolóállás jön létre]
2.A pörgetés után fogjunk meg három nem egymás mellettit, és állítsuk 2-re, ha nem az volt!
A lehetséges esetek:
hely----Biztos--------------------bizonytalan
1,3,5--1(2),2(2),3(2),5(2)--------4(1/2),6(1/2)
2,4,6--1(2),2(2),3(2),4(2),6(2)---5(1/2)
Tehát két pörgetés után mindkét esetben legalább egy bizonytalan helyem van. Innentől én is bizonytalan vagyok.
Mivel a pörgetés véletlenszerű kezdőpontú felállásokat hoz, elvben bármeddig pörgethetek, nézhetem, hogy van-e átállítandó (ha 1 akkor átállítom), de mi garantálja, hogy a három kezem közül valamelyik alá kerül a hátralévő (1 vagy 2) a maradék 3 pörgés alatt?
Nem látom értelmét annak sem, hogy az 1,2,3 és a 2,4,6 után egy újabb lépésvariációt vezessek be (mondjuk 1,2,4).
Ötlet?
|
 |
| Előzmény: [1647] magusocska, 2006-12-21 10:52:17 |
|
|
| [1647] magusocska | 2006-12-21 10:52:17 |
 Csernobili probléma néven a 81.-eshez hasonlót adtak fel a lányomnak az iskolába, de 6 lyuk és 3 kéz (sic!) esetén. Ez lehet 81/a vagy valami újabb, de a lényeg, hogy van-e ötletetekt ötlépéses megoldásra, vagy annak cáfolatára.
|
|
|
| [1645] JBence | 2006-12-20 22:24:24 |
 Van egy jó kis feladatom, lehet hogy a logikához kellett volna írni de mindegy: Van egy kétkarú mérlegünk és 12 golyónk. A golyók közül egynek más a tömege mint a másik tizenegyé, de nem tudjuk hogy nehezebb vagy könnyebb. Állapítsuk meg 3 mérésből hogy melyik a rossz golyó és hogy könnyebb e vagy nehezebb. Sok sikert :)
|
|
|
|
| [1641] Python | 2006-12-18 10:28:18 |
 Amúgy ez volt a legnehezebb feladat amit benne találtam...
Szerintem az egész ovisoknak készül... :)
Én is ezt az ötöt találtam...
|
|
|
| [1639] jonas | 2006-12-17 18:44:04 |
 Na jó, ne vacakoljunk vele egyesével. A számítógép szerint az összes megoldás (zárójelek nélkül):
7+2-5+2+1=7
7-2+5-2-1=7
7*2-5-2*1=7
7*2-5-2/1=7
7/2+5/2+1=7
|
| Előzmény: [1638] jonas, 2006-12-17 18:39:02 |
|
|
|
|
| [1635] Python | 2006-12-17 15:27:38 |
 7(?)2(?)5(?)2(?)1=7, ahol (?) a négy alapművelet egyike. Mi állhat a kérdőjelek helyén? Zárójelek nincsenek, de sok megoldás van, keressük meg az összeset!
Medvesajtos dobozban lévő kártyán volt, "matematikai intelligencia" mérésére, és oda volt írva a hátuljára egy primitív megoldás, és mellette az, hogy "Lehet, hogy van más megoldás is..." ... Én eddig azon kívül négy megoldást találtam...
|
|
| [1634] Cckek | 2006-12-17 09:22:40 |
 Határozzuk meg azokat a természetes számokat melyekre fennáll:
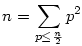 , ,
ahol p primszám.
|
|
|
| [1632] Csimby | 2006-12-16 18:29:48 |
 Ugyanaz a trükk mindkettőre úgyhogy sztem aki az egyiket meg tudja csinálni az a másikat is.
|
|
| [1631] jonas | 2006-12-16 18:13:03 |
 Négy számnál valószínüleg csak három műveletet használsz fel, így nehéz lenne mind a négyet használni.
Én az elsőt ismerem, a másodikat (3 3 8 8) pedig megoldotta az a program amit régen írtam az elsőre. (A megoldás a képen van.)
|
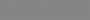 |
| Előzmény: [1629] Cckek, 2006-12-16 16:00:11 |
|
|
|
|
| [1627] Csimby | 2006-12-16 02:54:25 |
 302.feladat Adott a következő négy szám: 1,3,4,6. A négy alapművelet és a zárójelezés segítségével, mindegyik számjegyet egyszer felhasználva állítsuk elő a 24-et. (aki ismeri az NE lője le a megoldást)
|
|
|
|
|
|
| [1622] HoA | 2006-12-15 11:45:50 |
 Arra azért kíváncsi lennék, a hozzászólók hány százaláka leplezi le az ezoterikus parapszichológiai telepátiát. Mert az ilyen hozzászólást természetesen nem teszi fel a lapra. A "Minden jog fenntartva" témában is lennének aggályaim, ezt már máshol is láttam, például itt:
http://brutalvideos.freeweb.hu/Flash/psychic.htm
|
| Előzmény: [1614] Hajba Károly, 2006-12-14 08:04:24 |
|
|
|
| [1619] HoA | 2006-12-15 11:23:18 |
 Szerintem az ilyen, még fejben/papíron leszámolható eredményre vezető feladatokat úgy célszerű megoldani, hogy a lehetséges eseteket egy olyan döntési fa mentén derítjük fel, ahol a szimmetrikus esetek azonos ágra kerülnek. Esetünkben például: Van-e színezett saroknégyzet? Színezett-e a középső?
Ha valakinek 22-nál több vagy kevesebb jött ki, itt egy kis ellenőrzési lehetőség. Vagy javítsatok, ha én szúrtam el valamit :-)
|
 |
| Előzmény: [1617] Csimby, 2006-12-15 01:12:24 |
|
|
|
| [1616] Hajba Károly | 2006-12-14 22:25:52 |
 Ha egy színnel színezek, akkor, ha nem néztem el valamit, 20. S ebből következtetve 2 szín esetén kevesebb, mint 280, a szimmetrikus alakzatokban fellépő ismétlődések miatt. 4 szín esetén kevesebb, mint 480.
|
| Előzmény: [1615] Csimby, 2006-12-14 21:02:24 |
|
| [1615] Csimby | 2006-12-14 21:02:24 |
 301. feladat Egy 3×3-as négyzet 1×1-es kisnégyzetei közül hányféleképpen színezhetünk ki 4-et úgy, hogy a négyzet szimetriával egymásba vihető színezéseket nem tekintjük különbözőnek.
|
|
|
|
| [1612] psbalint | 2006-12-13 20:16:58 |
 http://www.asztralfeny.hu/magus/magus.php
egy kis izgalmas sziget a gyilkos feladatok végtelen óceánján... ;)
|
|
| [1611] Cckek | 2006-12-12 18:29:35 |
 Határozzuk meg az elipszis racionális kordinátájú pontjait:)
|
|










 ):=x2+y2+
):=x2+y2+ 0 , y
0 , y alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y
alakú tartomány harmadik csúcsát jelóli ki, de itt persze nincs maximum. Visszatérve eredeti feladatunkra, itt az x+y 100 és z+t+u+w
100 és z+t+u+w
 ,tg
,tg
 Q.
Q. 
 és
és 



 R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
R nemnegatív függvény, ami folytonosan deriválható. (Itt f-re úgy gondolok, mint a sebességre az idő függvényében, persze nem biztos, hogy ez a legcélszerűbb szereposztás.) f(a)=f(b)=0, mert az állomásokon áll a vonat. Menet közben is megállhat persze. f deriváltja korlátos, mert a vonat nem gyorsulhat akármennyivel. f integrálja a-tól b-ig (= a megtett út) adott. Kérdés, mennyi lehet f maximuma [a,b]-n.
 szerint periodikus, így ha találunk egy megoldást, akkor ahhoz 2
szerint periodikus, így ha találunk egy megoldást, akkor ahhoz 2 . És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)
. És mivel cos 120o=-1/2, ezért jelen esetben a2=b2+c2+bc. Várjuk a további konkrét kérdéseket :-)
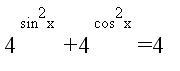
 b: $a \neq b$
b: $a \neq b$  b: $a \equiv b$
b: $a \equiv b$ 

 minden n>N-re a folytonosság miatt, ezért bn/2-
minden n>N-re a folytonosság miatt, ezért bn/2- , azaz
, azaz