Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[1013] Yegreg

2005-08-15 20:58:07

Üdv!

Bocs, hogy csak most írok, de most értem haza, így nem tudtam reagálni a közbenső dolgokra. A beírt gömb sugara jogos, az egyenletet nem ismertem, kitalálni meg akkor este esélyem sem volt, pláne, hogy nem is gondolkoztam ilyesmiben(a bizonyítás amúgy nagyon szép szerintem). A sok számolás azért nem annyira sok, csak egy finom túlzás volt annak eltitkolása érdekében, hogy képtelen lettem volna beírni akkor este:). Valójában azt hiszem, hogy az pár Pitagorasz-tétel volt.

Az a hatszöges feladat nem akar összejönni Viktornak:) Vagy direkt csináltad először nem létezőre másodjára pedig több esetesre? Szóval a 186(azt hiszem) feladat megoldása:

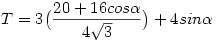
$T=3\big(\frac{20+16cos\alpha}{4\sqrt3}\big)+4sin\alpha$

Ahol alfa valamelyik belső szög. A 120°-os forgásszimmetria nem határozza meg egyértelműen a hatszöget, csak 3-3 belső szöge egyenlő egymással, két különböző belső szög összege pedig 240°. Egyébként szerintem a feladat normálisan körbe írt hatszög lenne. Akkor egyértelműen $\alpha$ =120°, és akkor kiszámolható a terület(akkor máshogy is számolható). Üdv:

Yegreg

[1012] xviktor

2005-08-14 17:59:30

Gratulalok, mindenki megoldasa helyes. De a 186. feladatra meg nem jott megoldas...

Jo gondolkozast: Viktor

[1011] lorantfy

2005-08-14 16:26:14

185-höz: Kössük össze a poliéder csúcsait a beírt gömb középpontjával. Így a poliéder térfogatát sokszög alapú gúlák térfogatának összegére bontottuk, melyek magassága éppen a beírt kör sugara, alapjaik területének összege pedig a poliéder felszine.

Igy aztán: 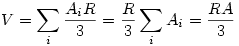$V=\sum_{i} \frac{A_iR}{3}=\frac{R}{3}\sum_iA_i=\frac{RA}{3}$

Előzmény: [1010] xviktor, 2005-08-13 01:19:00

[1010] xviktor

2005-08-13 01:19:00

Gratulalok szepek a megoldasaid /181,182,183/, a 184-et meg atgondolom en kicsit maskepp csinaltam,de szerintem az is jo.

A 183. feladatnal irtad hogy sok szamolas volt, pedig nagyon egyszeruen meg lehet allapitani a beirt gomb sugarat:

Tetel: Barmely poliederbe beirt gomb sugara: 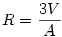$R=\frac{3V}A$

185. feladat: Bizonyitsuk be a fenti tetelt.

186. feladat: A 181. feladatot kisse fogalmazzuk at. Ha ahelyett hogy kor irhato bele azt mondanam, hogy 120°os forgasszimmetrikus, akkor mekkora lenne a terulete? /Ilyen hatszog letezik ;-)/

Jo gondolkodast: Viktor

Előzmény: [1009] Yegreg, 2005-08-13 00:49:02

[1009] Yegreg

2005-08-13 00:49:02

181.:

Ilyen hatszög nem nagyon van, hiszen ha egy 2 egység hosszú oldalt a kör x-re és 2-x-re bont, akkor az az x melletti 4 egység hosszú oldalt x-re és 4-x-re bontja, hiszen a körhöz külső pontból húzott érintő szakaszok egyenlőek, illetve továbblépve a 4-x melletti 2 egység hosszú oldalra, azt a körnek 4-x és 2-(4-x)-re kell bontania, szintén az érintő szakaszok miatt, azonban 2-(4-x)=x-2, csak akkor pozitív, ha x nagyobb, mint kettő, x azonban nem lehet nagyobb kettőnél, mert akkora szakaszt metszett le a kör egy másik két egység hosszú oldalból, tehát ha a beírt kör nem mehet át csúcson(azaz azt a sokszög teljes egészében tartalmazza), akkor nincs ilyen hatszög.

182:

2⁰ 3-as maradéka 1, 2¹-é 2, és belátható, hogy innentől kezdve periodikus, hiszen a 2 kétszerese mindig 4, aminek a 3-as maradéka mindig egy, az 1 kétszerese pedig mindig 2, aminek a 3-as maradéka kettő, ezzel a ciklus végére értünk. Látható tehát, hogy minden páratlan kitevő esetén 2 a hármas maradék. A 2³³³+2⁵⁵⁵-1 esetében a két kettő hatvány kitevője páratlan, hármas maradékuk 2 és 2, ezek összege 4, mínusz egy az 3, tehát az összeg osztható 3-mal, és mivel nagyobb nyilván, mint három, így nem lehet prím.

183:

Sok számolgatással(amit most nem szeretnék leírni, mert úgyis félreírnám) megkapjuk, hogy szabályos tetraédernél:

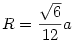
$R=\frac{\sqrt{6}}{12}a$

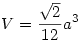
$V=\frac{\sqrt{2}}{12}a^3$

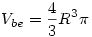
$V_{be}=\frac43 R^3 \pi$

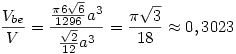
$\frac{V_{be}}{V}=\frac{\frac{\pi 6\sqrt{6}}{1296}a^3}{\frac{\sqrt{2}}{12}a^3}=\frac{\pi \sqrt{3}}{18}\approx 0,3023$

184:

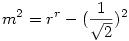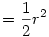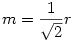Ha összekötjük a négy alsó gömb középpontját a vele szomszédosokkal, valamint az alsó 4-ét a felsőjével, akkor egy négyzet alapú gúlát kapunk, aminek minden oldala R.(ezt be lehet látni, hiszen érintik egymást) Ennek a gúlának a magassága $m^2=r^r-(\frac1{\sqrt{2}})^2$ (Pitagoras tétel alapján) $=\frac12 r^2$ Ebből $m=\frac1{\sqrt{2}} r$ Amiből ha meg akarjuk kapni a földtől való tárvolságot, akkor még hozzá kell adni $\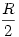frac{R}2$ , hiszen a gúla ilyen magasan van, ekkor tehát az 5. gömb távolsága a talajtól:

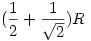
$(\frac12 +\frac1{\sqrt{2}})R$

És azt hiszem, ennyi feladat volt. Bocsánat, hogy 1, nincs ábra 2, nincs túl sok számolás leírva 3, ha valahol számolási hibát vétettem , de késő van már.

Üdv:

Yegreg

[1008] xviktor

2005-08-12 16:41:51

Mostanaban hallottam par jo kis feladatot, gondoltam beirok ide parat.

181. feladat: Van egy hatszog mely oldalai: 2,4,2,4,2,4 /ebben a sorrendben/. Mekkora a hatszog terulete, ha tudjuk, hogy kor irhato bele?

182. feladat: Kicsit maskepp irom be ide mint az eredeti feladatban szerepel, hogy szamologepet ne lehessen hasznalni: Bizonyitsuk be hogy 2³³³+2⁵⁵⁵-1 nem prim!

183. feladat: Van egy szabalyos tetraederunk. A tetraederbe irt gomb terfogata hany szazaleka a tetraeder terfogatanak?

184. feladat: Van negy ugyanakkora sugaru gomb, melyek egy vizszintes asztalon paronkent erintik egymast. Pontosan kozepre "felrakunk" egy 5., a lentiekkel megegyezo sugaru gombot. Milyen messze van a fenti gomb kozeppontja a talajtol?

Jo gondolkodast!

[1007] xviktor	2005-08-09 00:04:41
Most akkor jo a megoldasom?
Előzmény: [1006] jonas, 2005-08-08 23:19:43

[1006] jonas	2005-08-08 23:19:43
Persze konstans nélkül nem is lenne értelme, mert úgy csak páratlan függvények állhatnak elő.
Előzmény: [1005] jonas, 2005-08-08 23:00:55

[1005] jonas	2005-08-08 23:00:55
Konstansokat (mint az 1) lehet használni? Én eddig úgy hittem, hogy nem.
Előzmény: [1002] xviktor, 2005-08-08 17:12:05

[1003] xviktor

2005-08-08 18:23:15

Az egesz levezetese sztem:

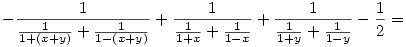
$-\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+\frac1{\frac1{1+x}+\frac1{1-x}}+\frac1{\frac1{1+y}+\frac1{1-y}}-\frac12=$

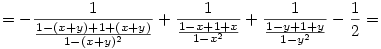
$=-\frac1{\frac{1-(x+y)+1+(x+y)}{1-(x+y)^2}}+\frac1{\frac{1-x+1+x}{1-x^2}}+\frac1{\frac{1-y+1+y}{1-y^2}}-\frac12=$

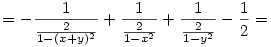
$=-\frac1{\frac2{1-(x+y)^2}}+\frac1{\frac2{1-x^2}}+\frac1{\frac2{1-y^2}}-\frac12=$

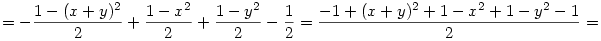
$=-\frac{1-(x+y)^2}2+\frac{1-x^2}2+\frac{1-y^2}2-\frac12=\frac{-1+(x+y)^2+1-x^2+1-y^2-1}2=$

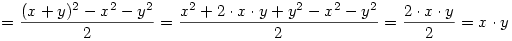
$=\frac{(x+y)^2-x^2-y^2}2=\frac{x^2+2\cdot x\cdot y+y^2-x^2-y^2}2=\frac{2\cdot x\cdot y}2=x\cdot y$

Amennyiben elirtam valamit legyszives szoljatok.

Udv: Viktor

u.i.: megtalaltam a szorzas jelet :)

[1004] xviktor

2005-08-08 17:42:52

Az x*y fuggvenyt a kovetkezokepp lehet megcsinalni szerintem:

$\frac{(-2*\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+1)-(-2*\frac1{\frac1{1+x}+\frac1{1-x}}+1)-(-2*\frac1{\frac1{1+y}+\frac1{1-y}}+1)}2$

Itt kettovel lehet egyszerusiteni:

$(-\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+\frac12)-(-\frac1{\frac1{1+x}+\frac1{1-x}}+\frac12)-(-\frac1{\frac1{1+y}+\frac1{1-y}}+\frac12)$

Bontsuk fel a zarojeleket:

$-\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+\frac12+\frac1{\frac1{1+x}+\frac1{1-x}}-\frac12+\frac1{\frac1{1+y}+\frac1{1-y}}-\frac12=$

$=-\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+\frac1{\frac1{1+x}+\frac1{1-x}}+\frac1{\frac1{1+y}+\frac1{1-y}}-\frac12$

Igy a megoldas szerintem:

$x*y=-\frac1{\frac1{1+(x+y)}+\frac1{1-(x+y)}}+\frac1{\frac1{1+x}+\frac1{1-x}}+\frac1{\frac1{1+y}+\frac1{1-y}}-\frac12$

Előzmény: [1002] xviktor, 2005-08-08 17:12:05

[1002] xviktor

2005-08-08 17:12:05

Az x² fuggvenyt a kovetkezokepp lehet megcsinalni szerintem:

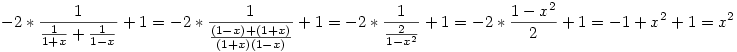$-2*\frac1{\frac1{1+x}+\frac1{1-x}}+1=-2*\frac1{\frac{(1-x)+(1+x)}{(1+x)(1-x)}}+1=-2*\frac1{\frac2{1-x^2}}+1=-2*\frac{1-x^2}2+1=-1+x^2+1=x^2$ .

Miutan megvan x² Jonas modszerevel megvan x*y fuggveny is.

Udv: Viktor

u.i.: Legyszives segitsetek, hogy szorzas jelet hogy lehet beirni TeXben? Elore is koszi.

Előzmény: [1001] rizsesz, 2005-08-08 16:28:41

[1001] rizsesz	2005-08-08 16:28:41
Tyű, köszönöm :) a négyzet viszont számomra elérhetetlennek tűnik a páratlan kitevők miatt :( Engem is az gátolt meg eddig, és közeledek. :) segítsééééég!

[1000] jonas

2005-08-08 15:35:15

Ezt a feladatot már hallottam, de nem tudom a teljes megoldást.

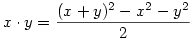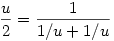
A segítség az volt hozzá, hogy állítsuk elő a négyzetre emelést először. Ha az már megvan, akkor $x \cdot y = \frac{(x + y)^2 - x^2 - y^2}2$ ; ahol kettővel osztani tudunk, mert $\frac u2 = \frac 1{1/u + 1/u}$

Most azt kéne megpróbálni, hogyan lehet x²-et előállítani. Eddig nem tudom, hogyan lehet, de még gondolkodom rajta.

Valami olyasmit kell használni, hogy 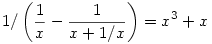$1/\left( \frac 1x - \frac 1{x + 1/x} \right) = x^3 + x$ ...

Előzmény: [989] rizsesz, 2005-08-06 21:42:56

[999] rizsesz	2005-08-07 16:46:16
1000.

[998] rizsesz

2005-08-07 16:46:03

(elnézést, zárójelezgetni is lehet). tehát mondjuk előállítható az 1/(x+y) kifejezés, x-2y, stb, míg azonban n*m esetén nem jó az m+m+m+m...+m (n-szer) (n és m valós szám). tehát összegezve valami olyasmi a feladat, hogy lehetséges-e két számot összeszorozni csak a +, - és 1/x műveletek segíségével úgy, hogy bármely két szám esetén mindig ugyanazokat a műveleteket hajtjuk végre (mintha egy képletbe helyettesítenénk be) függetlenül a két számtól.

[997] Yegreg

2005-08-07 16:07:05

Tehát egy olyan polinomra gondolsz, ahol x és y csak 1 és -1 hatványon lehet, és az együttható is csak 1 vagy -1 lehet mindenhol? Valamint a tagok száma véges, és nem változóval kifejezhető?

Érdekes feladat így.

Üdv

Yegreg

[996] rizsesz	2005-08-07 15:58:06
Igen, de csak a fenti 3 dolgot lehet használni.
Előzmény: [995] xviktor, 2005-08-07 15:00:06

[995] xviktor	2005-08-07 15:00:06
Akar tortet is hozza lehet adni?
Előzmény: [994] rizsesz, 2005-08-07 14:58:22

[994] rizsesz	2005-08-07 14:58:22
Pontosan. Tehát az x*y kifejezést kell előállítani x-k, y-k, +, - és a reciprok műveletek segítségével.
Előzmény: [993] Gubbubu, 2005-08-07 14:43:34

[993] Gubbubu	2005-08-07 14:43:34
És ha jól értem, egyáltalán szorzás sem szerepelhet a célkifejezésben ( pl. (x+y)*(x+y) )?
Előzmény: [992] Gubbubu, 2005-08-07 14:33:10

[992] Gubbubu	2005-08-07 14:33:10
Kapcsos zárójel (ti. olyasmi, mint az informatikában az IF vagy a CASE műveletek) szerepelhet? És "végtelen sok kapcsos zárójel" :-?
Előzmény: [991] Gubbubu, 2005-08-07 14:31:48

[991] Gubbubu	2005-08-07 14:31:48
Ha jól értem, az x és y változók szorzatát (nem a hatványát, ugye?)?
Előzmény: [989] rizsesz, 2005-08-06 21:42:56

[990] Yegreg

2005-08-06 22:41:45

Kedves Péter!

Kössz a címet, de én jobban megértem a saját gondolatmenetem alapján. Az már kiderült számomra, hogy az n dimenziós általánosítás helyes, mert megkérdeztem valakitől, és az mondta, hogy összegezni kell váltott előjellel a különböző dimenziós felületek számát -1-től n-ig(n dimenzióban), és 0 kapunk.(negatívval kezdjük)., Valamint, hogy a -1 dimenziós felületek száma mindig 1, és az n dimenziósé is.

És ha megnézzük, akkor ez pontosan ugyanaz, mint az enyém, egy kis átalakítás után.

Szóval, örülök, hogy rájöttem, és szeretném bizonyítani az én gondolatmenetem, legfeljebb majd utána elolvasok más gondolatmeneteket és bizonyításokat is.

Bár a nem egyszereű poliéderekre vonatkozó általánosítás helyességéről még nem kaptam visszajelzést(igaz, azt a részt magam is bizonyítottam, csak ide nem írtam le), de eddig minden egyes esetben helyes eredményt adott, bár megjegyezték, hogy néha talán nehezen használható. Valójában nem annyira, szerintem, de ez további gondolkodásra késztetett.

ScarMan barátom említette, hogy ismer egy c+l=e+2-2*k képletet, k lyukú tórusszal ekvivalens alakzatokra, ami nyilván adott esetben könnyebben használható, mint az enyém, ezekután gondoltam arra, hogy talán a speciális tulajdonságokat(ami jelen esetben a tórusz-ekvivalencia) beírva a képletbe, megkaphatjuk a speciális formulát.

Az ötlet helyesnek bizonyult, a tóruszoknál legalábbis biztosan. Ha a legvégsőként beírt képletet nézitek... Az egyszerű poliéderek száma, melyekre felbontjuk a tóruszt k. Jelen esetben k=1(ez most nem a lyukak száma, csak a képletben volt így), méghozzá egy véges henger, ha úgy tetszik gömb, amire a "standard" Euler tétel vonatkozik. A tóruszt minden lyukánál található gyűrűben "elvágjuk", így nyilván gömbbel ekvivalens alakzatot kapunk, az egyszerű poliéder pedig önmagával érintkezett akárhány csúcson és ugyanannyi élen, ezek a képletben kiejtik egymást, valamint minden egyes lyuk körüli gyűrűben pontosan két lapon(a vágás mentén, ha úgy tetszik), és mivel k(visszatérva ScarMan képletéhez, bocs, hogy a k-t két dologra használtam) lyukú tóruszról volt szó, így egy 2*k a bal oldalon, ezt ha átvisszük a jobb oldalra, akkor látható, hogy a barátom által említett c+l=e+2-2*k képletet kapjuk, tehát az általam felírt képlet alkalmas speciális esetekre vonatkozó egyenletek levezetésére.

Tulajdonképpen, feltehetőleg ekvivalens a Péter által írt címen található képlettel, csak ahhoz jobban meg kellene nézni.

Igazából azért írtam le a képletet, mert a gondolatmenetem bizonyítására vártam ötleteket, nem azért, hogy leírjátok az általános Euler tételt, mert ez már az. Csak esetleg más alakban, mint ismeritek.

Ha bizonyításként az választjátok, hogy leírjátok a ti képletetek levezetését, és belátjátok, hogy az ekvivalens az enyémmel, az elfogadható, bár mint már mondtam, nekem most nem ez lenne a célom, pontosan ezért nem néztem meg könyvben sem, mert hajlamos lennék én is így letudni, ahelyett, hogy a saját gondolatmenetemet bizonyítanám.

Üdv

Yegreg

[989] rizsesz	2005-08-06 21:42:56
Sziasztok, egy elég meglepő probléma ütött szöget a fejembe: elő kellene állítani az f(x;y)=xy függvényt az összeadás, kivonás és reciprok műveletek segítségével, de természetesen nem jó az x szerepeljen y alkalommal :) szóval valahogy elő kellene állítani xy-t :)

Már regisztráltál?
Új vendég vagy?