Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[1194] Lóczi Lajos

2006-03-14 23:58:40

Valóban, úgy tűnik, Volterra csinált először ilyet Riemann integrálra (ami után persze adtak később egyszerűbb példákat is). A konstrukció lényege, hogy a korlátos derivált (mértékelméleti szempontból) túl sok helyen szakad: egy "kövér" Cantor-halmazon, az ilyeneket pedig Riemann nem tudja visszaintegrálni.

A feladatban viszont nem mondtam meg, milyen integrált használjunk.

220. feladat. U. az, mint a 217. feladat, csak az integrált értsük Lebesgue értelemben.

Ez a feladat jóval könnyebb, mint a Riemannos megfelelője, és az előzetes integrálos kérdések pont ezt készítették elő.

Fontos adalék, hogy Lebesgue (1900-as évek eleje) után fél évszázaddal kidolgozták a Henstock-Kurzweil integrált, amelynek definíciója formailag alig különbözik Riemannétól, és azzal a jó tulajdonsággal bír, hogy minden [a,b] intervallumon értelmezett deriváltat vissza tud integrálni (tehát a 217. feladatbeli formulában mindig egyenlőség áll), sőt egyúttal minden, [a,b]-n Lebesgue-integrálható függvényt is tartalmaz. Ezt az integrálfogalmat nyugodtan lehetne Riemann helyett tanítani, mert a bizonyítások csak alig bonyolultabbak és cserébe sokkal többet kapunk.

Előzmény: [1191] nadorp, 2006-03-14 20:43:23

[1193] Lóczi Lajos	2006-03-14 23:38:41
Pont ezekre a kis átalakítgatásokra gondoltam :)
Előzmény: [1192] ágica, 2006-03-14 22:50:28

[1192] ágica	2006-03-14 22:50:28
Vagy pedig, mivel g(x) csupán egy 1/ $\pi$ -s szorzóban különbözik az n-edik Bessel-függvénytől, melyre szintén teljesül ugyanez a differenciálegyenlet, így megoldható a feladat a Bessel-függvényekre vonatkozó bizonyítással teljesen analóg módon is (g(x) deriváltját számolva, majd parciálisan integrálva egy kis alakítgatás után kijön az egyenlet).
Előzmény: [1189] Lóczi Lajos, 2006-03-13 22:50:30

[1191] nadorp	2006-03-14 20:43:23
Két helyen is találtam példát, mindkettő Volterra konstrukcióját közli. Azt látja be, hogy létezik olyan [0,1]-en mindenhol differenciálható függvény, melynek derivált függvénye korlátos, de nem Riemann integrálható.
Előzmény: [1188] Lóczi Lajos, 2006-03-13 22:41:14

[1190] lgdt	2006-03-14 02:02:55
kiegészítés: azt észreveszed, ha kinyírtad, végtelen sok időd van a lövöldözésre/csapkodásra.
Előzmény: [1183] lgdt, 2006-03-10 19:19:16

[1189] Lóczi Lajos

2006-03-13 22:50:30

A deriválásokat elvégezve, ebben a feladatban nyilván csak annyit kell bizonyítani, hogy az y-szerinti integrálja 0-tól $\pi$ -ig az alábbi kifejezésnek

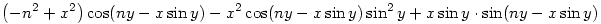
$\left( -n^2 + x^2 \right) \cos (ny - x\sin y) - x^2\cos (ny - x\sin y)\sin^2 y + x\sin y\cdot \sin (ny - x\sin y)$

éppen nulla, ha n egész szám és x valós szám.

Előzmény: [1184] Lóczi Lajos, 2006-03-10 23:10:59

[1188] Lóczi Lajos

2006-03-13 22:41:14

Trükkös. Akkor a következő kérdés természetesen az, hogy

Van-e példa vajon olyan F függvényre, ami a zárt [0,1] intervallumon mindenhol értelmezve van, mindenhol deriválható, de az idézett Newton-Leibniz-formula nem igaz rá?

Előzmény: [1186] ágica, 2006-03-13 19:39:06

[1187] Csimby

2006-03-13 19:56:42

218. feladat Az Euler-féle poliéder-tétel ugyenbár csak "nem lyukas" testekre igaz. Hogy-néz ez ki "k lyukú testek" (k=1: tórusz, k=2: kengyel-felület) esetében?

219. feladat Adott a gömbön egy térkép országokkal és a fővárosaikkal. Vegyük azt a gráfot, aminek csúcsai a fővárosok, és két csúcsot pontosan akkor kötünk össze, ha a nekik megfelelő fővárosok országai határosak. Mondjunk olyan testet minden k-ra, hogy a testre lehessen olyan térképet rajzolni, amihez az előbbi módon definiált gráf a teljes k csúcsú gráf.

[1186] ágica	2006-03-13 19:39:06
Hát, ha ér olyan példát mondani amire az egyenlőség már csak azért sem teljesülhet, mert a függvény nincs értelmezve nullában, akkor pl F(x)=ln x. :)
Előzmény: [1185] Lóczi Lajos, 2006-03-12 01:59:04

[1185] Lóczi Lajos	2006-03-12 01:59:04
217. feladat. Adjunk példát (ha van) olyan F valós függvényre, amely deriválható az egész (0,1) intervallumon, de 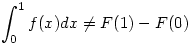$\int_0^1 f(x) dx\ne F(1)-F(0)$ , ahol f=F'.

[1184] Lóczi Lajos

2006-03-10 23:10:59

216. feladat. Legyen n egész szám, x pedig valós szám. Igazoljuk, hogy az

x²g''(x)+xg'(x)+(x²-n²)g(x)=0

(differenciál)egyenlet egy megoldása a

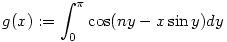$g(x):=\int_0 ^\pi \cos(n y-x \sin y) dy$ függvény.

[1183] lgdt

2006-03-10 19:19:16

1. egy koordinátarendszerben egy láthatatlanul kicsi bolha minden másodperc elején mindig ugyanazzal az egész koordinátájú vektorral ugrik odébb (az origóból indul). tetszőleges egész koordinátájú pontjára lőhetsz minden másodperc végén.

2. a számegyenesen az origóból kiindulva mindig ugyanakkora valós számmal ugrik odébb. egy egységnyi szélességű vonalzóval csapkodhatsz minden ugrás után.

3. a síkon az origóból indulva mindig ugyanazzal a valós koordinátájú vektorral ugrik odébb, és egy négyzet alakú pecsét áll a rendelkezésedre.

Melyik esetben tudod kinyírni a bolhát és ha igen, hogyan?

Sorry a megfogalmazásért, valahogy így hangzott el előadáson is. Esetleg valaki átfogalmazhatná.

[1182] Lóczi Lajos	2006-03-09 10:50:41
Én is így gondolom.
Előzmény: [1180] nadorp, 2006-03-09 00:11:07

[1181] Fálesz Mihály	2006-03-09 10:15:52
A (c) feladatban nem nehéz felírni a primitív függvényt.
Előzmény: [1169] Lóczi Lajos, 2006-03-07 00:25:21

[1180] nadorp

2006-03-09 00:11:07

Csatlakozom Jonashoz. Ha egy függvény Lebesgue-integrálható, akkor ha jól tudom, az abszolútértéke is az. Ezért, ha k>0 egész és $a<\frac\pi2$ valós szám, akkor

$\int_{\frac1{k\pi}}^{\frac1{(k+1)\pi}}\left|\frac1xsin\frac1x\right|dx=\int_{k\pi}^{(k+1)\pi}\left|\frac{sin~x}x\right|dx>\int_{k\pi+a}^{(k+1)\pi-a}\left|\frac{sin~x}x\right|dx>(\pi-2a)\frac{|sin~a|}{(k+1)\pi-a}$ .

Ebből már "látszik", hogy a Lebesgue szerinti integrál nem létezhet, mert a harmonikus sor divergens. Visszatérve még az eredeti példára, az $\int_0^1\frac1{x^\alpha}sin\frac1xdx$ Riemann improprius integrál - ha el nem számoltam - pontosan $\alpha$ <2 esetén létezik

Előzmény: [1178] Lóczi Lajos, 2006-03-08 21:20:15

[1179] jonas	2006-03-08 21:46:15
Gondolom, akkor a (b) sem létezik.
Előzmény: [1178] Lóczi Lajos, 2006-03-08 21:20:15

[1178] Lóczi Lajos	2006-03-08 21:20:15
215. feladat. A kérdés ugyanaz, mint a 214-esben, csak az integrálokat ne improprius Riemann, hanem Lebesgue értelemben értsük.

[1177] lgdt	2006-03-08 20:32:35

Előzmény: [1171] ágica, 2006-03-07 21:49:49

[1176] Lóczi Lajos	2006-03-08 18:36:33
Persze, hogy jó, hiszen az abszolút konvergencia az improprius integrálok esetén is maga után vonja a konvergenciát (Cauchy-kritérium).
Előzmény: [1171] ágica, 2006-03-07 21:49:49

[1175] nadorp

2006-03-08 16:17:05

b) Az 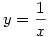$y=\frac1x$ helyettesítéssel az integrál a következő alakú lesz

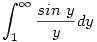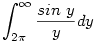$\int_1^{\infty}\frac{sin~y}ydy$ . Nyilván elég az $\int_{2\pi}^{\infty}\frac{sin~y}ydy$ integrállal foglalkozni. Ezt a következőképpen érdemes felírni:

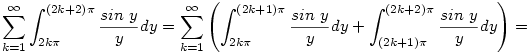
$\sum_{k=1}^{\infty}\int_{2k\pi}^{(2k+2)\pi}\frac{sin~y}ydy=\sum_{k=1}^{\infty}\left(\int_{2k\pi}^{(2k+1)\pi}\frac{sin~y}ydy+\int_{(2k+1)\pi}^{(2k+2)\pi}\frac{sin~y}ydy\right)=$

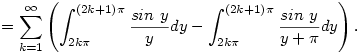
$=\sum_{k=1}^{\infty}\left(\int_{2k\pi}^{(2k+1)\pi}\frac{sin~y}ydy-\int_{2k\pi}^{(2k+1)\pi}\frac{sin~y}{y+\pi}dy\right).$

Innen már sejthető, hogy a fenti összeg becsülhető a 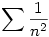$\sum\frac1{n^2}$ sorral, ami konvergens

Előzmény: [1169] Lóczi Lajos, 2006-03-07 00:25:21

[1174] hobbymatekos	2006-03-08 14:07:19
Vagyis én tévedtem el.
Előzmény: [1173] hobbymatekos, 2006-03-08 11:57:01

[1173] hobbymatekos	2006-03-08 11:57:01
Rendben. Akkor egyetlen mondattal megjavitom azt a bizonyitást. Bizonyitás: kontradikció .... Qed A pontok közötti rész jó.
Előzmény: [1170] jenei.attila, 2006-03-07 11:15:33

[1172] nadorp	2006-03-08 08:43:34
Szerintem jó ( bár ez nem jelent semmit). Sajnos b) és c) esetekre nem alkalmazható.
Előzmény: [1171] ágica, 2006-03-07 21:49:49

[1171] ágica

2006-03-07 21:49:49

a)-ra egy ötlet, de nem tudom, hogy jó-e: mivel

$\big|\frac{1}{\sqrt{x}}\sin\frac{1}{x}\big|\le\frac{1}{\sqrt{x}},$

és

$\int_0^1\frac{1}{\sqrt{x}}dx=2,$

ezért az eredeti integrál is véges.

Előzmény: [1169] Lóczi Lajos, 2006-03-07 00:25:21

[1170] jenei.attila	2006-03-07 11:15:33
Tényleg túl bonyolítod (vagy nem érted) a dolgot. Attól, hogy az együtthatók és p, q lehetnek negatívak is,ugyanúgy érvényesek Iván88 meggondolásai (van értelme negatív egészek paritásáról beszélni). Igen, negatív számok páratlan hatványa negatív, de akkor mi van? Össze tudunk adni pozitív és negatív számokat. A középső + jellel végképp nem értem mi bajod. Mennyiben más, ha a páratlan számot 2b-1 alakban írjuk fel, ugyanúgy 2b+1 alakban is megfelelő. Ne haragudj, de szerintem az ilyen hozzászólásod céltalan kötekedésnek minősíthető.
Előzmény: [1168] hobbymatekos, 2006-03-07 00:02:07

Már regisztráltál?
Új vendég vagy?