Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[1307] Virág	2006-07-16 16:20:33
Időközben megnéztem a F1-et, de érintőlegesen a feladaton is gondolkodtam.... :o) Nekem nagyon bonyolult, lehet, hogy nincs is erre konkrét képlet?
Előzmény: [1306] Sirpi, 2006-07-16 13:51:49

[1306] Sirpi	2006-07-16 13:51:49
Mondjuk ez a képlet tuti nem jó. Ha k=1, az azt jelenti, hogy legalább egy hosszú egyformákból álló blokk van, ennek esélye 1, nem pedig n/2^n-1. Ugyanúgy ha k=2, akkor az esély 1-1/2^n-1, nem pedig a képletből adódó (n-2)/2^n-1. Jó kérdés, hogy mi lehet a helyes képlet...
Előzmény: [1305] Virág, 2006-07-16 12:15:46

[1305] Virág	2006-07-16 12:15:46
Jaj köszi! :o)) Sajna a matek nem igazán az erősségem, de a feladat érdekel.
Előzmény: [1304] Sirpi, 2006-07-16 12:09:14

[1304] Sirpi

2006-07-16 12:09:14

Na, csak hogy rendesen meglegyen (még nem gondoltam bele, hogy jó-e a képlet, és eltartott vagy 2 percig, míg rájöttem, mi akar az ott lenni...). Tehát annak esélye, hogy lesz legalább k db. egyforma oldal n dobásból:

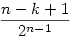
$\frac{n-k+1}{2^{n-1}}$

ami n=k-ra 1/2^n-1-et ad (legalább ez a része tuti jó :-) ).

Előzmény: [1303] Virág, 2006-07-16 11:29:29

[1303] Virág

2006-07-16 11:29:29

Sziasztok! Egy érdekes feladat, legalábbis nekem. Tudnátok segíteni? Egy pénzérmét feldobok "n"-szer. Mi a valószínűsége annak, hogy lesz legalább "k" darab egyforma dobás egymás után? (Tehát "k" darab fej, vagy "k" darab írás közvetlenül egymás után.)

Valaki szerint ez a képlet talán jó?

2*(n-k+1)/(2 n) Ha n=k, akkor lesz: 1/(2(k-1)) , ajaj nem tudok beírni egy jelet, de gondolom tudjátok.

[1302] nadorp	2006-07-12 08:27:07
Bocs, azért nem árt, ha feltesszük azt is,hogy b+c $\ge$ 2a
Előzmény: [1301] nadorp, 2006-07-11 14:47:24

[1301] nadorp

2006-07-11 14:47:24

Vagy egy kicsit még ragozva:

$c)~~\frac{x}{ax+by+cz}+\frac{y}{ay+bz+cx}+\frac{z}{az+bx+cy}\geq\frac3{a+b+c}$ , ahol a,b,c adott pozitív valós számok

Előzmény: [1300] Suhanc, 2006-07-11 10:16:01

[1300] Suhanc

2006-07-11 10:16:01

Kedves Mindenki!

Vérszemet kapva, a 236.feladat után szabadon:

237.Feladat Legyenek x, y, z, pozitív valós számok! Igazoljuk, hogy ekkor:

a) 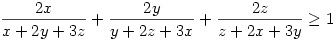$\frac{2x}{x+2y+3z} + \frac{2y}{y+2z+3x} + \frac{2z}{z+2x+3y} \ge 1$

b) 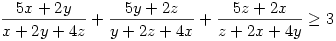$\frac{5x+2y}{x+2y+4z}+ \frac{5y+2z}{y+2z+4x}+ \frac{5z+2x}{z+2x+4y}\ge 3$

[1299] jonas

2006-07-07 13:01:35

A javított kód -- ha valakit még érdekel ezek után:

Ky8qLi8iMV0yPDovXCIxKDYkMTApIzoxZTV9LmkuMWU2CisvKi4vIjFdMjwv

XCIxKDYkMTApIzoxZTV9LmkuMWU2Cg==

Előzmény: [1284] jonas, 2006-06-21 12:24:22

[1298] jonas	2006-07-07 12:57:57
Aha. Valóban. Én beleszámoltam a hatjegyűnél rövidebbeket is (a szigorúan monoton esetben csak az ötjegyűeket), azért jött nekem ki $\binom{6}{10}$ illetve $\binom{6}{15}$ a helyes eredmény helyett. Hát ez buta hiba volt. Ráadásul kétszer is elkövettem, mert a binomiális együtthatókat is rögtön így írtam fel, és az összeszámláló kódot is.
Előzmény: [1296] Suhanc, 2006-07-05 22:33:44

[1297] lorantfy

2006-07-05 23:23:32

Szia Suhanc!

Kösz a megoldást! Valóban az ismétlés nélküli és az ismétléses kombináció tipikus esetei ezek a példák, csak erre nem olyan könnyű rájönni.

Még a 233. feladat maradt állva, de Sirpi [1289] segítségével remélem erre is vállalkozik valaki!

Előzmény: [1296] Suhanc, 2006-07-05 22:33:44

[1296] Suhanc

2006-07-05 22:33:44

Kedves László!

Ha nem olvastam figyelmetlenül a hozzászólásokat, a 234.feladat még él. Egy lehetséges megoldás:

a)Tegyük fel, hogy valaki odaad nekünk 6 különböző számjegyet, azzal a kéréssel, csináljunk belőle az a)-nak megfelelő hatjegyű számot. Ekkor a legkisebb számjegyet írjuk előre, utána a második legkisebbet... azaz, e 6 számjegyből pontosan egy, a feladat feltételeinek megfelelő szám készíthető. Azt kell még eldöntenünk, hány ilyen számjegyhatos választható ki. A számjegyeknek a szigorú monotonitás miatt kell különbözőeknek lenniük, és 0 nem szerepelhet közöttük, hiszen azt csak a legelső helyre írhatnánk, de 0-val nem kezdünk számot. Így 9 számjegyből kell 6 különbözőt kiválasztanunk. Ez 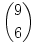$\binom{9}{6}$ féleképp tehető meg.

b) A feladat az a)-hoz hasonló, de itt "csak" monotonitás az elvárt, így azonos számjegyek is lehetnek, ám 0 itt sem. Tehát itt 9 számjegyből ismétléssel kell kiválasztanunk 6-ot. Az ismert módon ez 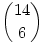$\binom{14}{6}$ féleképp tehető meg.

Előzmény: [1283] lorantfy, 2006-06-21 09:41:24

[1295] Suhanc

2006-07-05 19:47:19

Kedves Tibi!

Egy lehetséges megoldás a feladatodra:

Írjuk az egyenlőtlenség jobb oldalán az 1-ek helyére a+b+c+d-t:

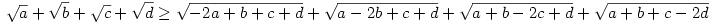
$\sqrt{a}+ \sqrt{b}+ \sqrt{c}+ \sqrt{d} \ge \sqrt{-2a+b+c+d} + \sqrt{a-2b+c+d} +\sqrt{a+b-2c+d} +\sqrt{a+b+c-2d}$

Legyen most

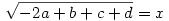
$\sqrt{-2a+b+c+d}=x$

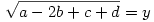
$\sqrt{a-2b+c+d}=y$

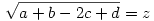
$\sqrt{a+b-2c+d}=z$

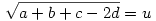
$\sqrt{a+b+c-2d}=u$

Ekkor:

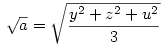
$\sqrt{a} = \sqrt{\frac{y^2+z^2+u^2}{3}}$

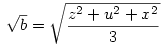
$\sqrt{b} = \sqrt{\frac{z^2+u^2+x^2}{3}}$

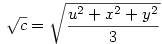
$\sqrt{c} = \sqrt{\frac{u^2+x^2+y^2}{3}}$

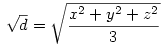
$\sqrt{d} = \sqrt{\frac{x^2+y^2+z^2}{3}}$

A bizonyítandó egyenlőtlenség ekkor:

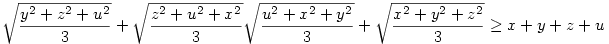
$\sqrt{\frac{y^2+z^2+u^2}{3}}+ \sqrt{\frac{z^2+u^2+x^2}{3}} \sqrt{\frac{u^2+x^2+y^2}{3}} +\sqrt{\frac{x^2+y^2+z^2}{3}} \ge x+y+z+u$

Nyilvánvaló, hogy x,y,z,u $\ge$ 0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk.

Egyenlőség x=y=z=u esetén lehetséges, melyből a=b=c=d szükséges és elégséges feltétel levezethető.

Előzmény: [1294] lorytibi, 2006-07-04 20:18:29

[1294] lorytibi

2006-07-04 20:18:29

Sziasztok!

Matektáborban voltam a múlt héten és van egy példa, amit nem tudtunk megoldani:

236. feladat: Bbh., ha $a,b,c,d \in \Big[0;\frac13 \Big]$ és a+b+c+d=1, akkor

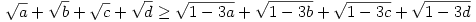
$\sqrt a+\sqrt b+\sqrt c+\sqrt d \ge \sqrt{1-3a}+\sqrt{1-3b}+\sqrt{1-3c}+\sqrt{1-3d}$

[1293] nadorp	2006-06-27 10:10:10
Gratulálok, ezt a megoldást ismertem én is. Az egy pontba való eltolást elegáns ötletnek tartom. Egyébként ez egy Kalmár példa volt pár évvel ezelőtt.
Előzmény: [1292] lorytibi, 2006-06-24 16:50:54

[1292] lorytibi	2006-06-24 16:50:54
235.feladat megoldása: Egy konvex kilencszögnek 27 átlója van. Mivel nincs két párhuzamos átló, ezért ha az átlókat az egyik metszéspontba toljuk, akkor 54 félegyenes indul ki a pontból, 54 szöget alkotva. Így a szögek átlaga 360°/54, ami biztosan kisebb 7°, tehát biztosan van két olyan átló, melyek egyenesei 7°-nál kisebb szöget zárnak be.
Előzmény: [1291] nadorp, 2006-06-23 08:34:47

[1291] nadorp

2006-06-23 08:34:47

Egy kis ujjgyakorlat.

235.feladat Egy konvex kilencszögnek nincs két párhuzamos átlója. Bizonyítsuk be, hogy van olyan két átló, melyek egyenesei 7^o-nál kisebb szöget zárnak be.

[1290] Yegreg

2006-06-21 23:17:56

És így nyilván, ha n relatív prím 10-hez, akkor van csupa 1-esből álló többszörös. Lehet kicsit általánosítani:

pl.: milyen n számokra létezik n-nek olyan többszöröse, mely k-s számrendszerben csak m-es jegyeket tartalmaz? (0<m<k nyilván)

[1289] jonas	2006-06-21 17:46:42
Jaj, tényleg. Ez sokat segített. Így már tudom a megoldást.
Előzmény: [1288] Sirpi, 2006-06-21 17:28:33

[1288] Sirpi	2006-06-21 17:28:33
233-nál több is igaz: Minden pozitív egésznek van olyan többszöröse, ami 11...100...0 alakú.
Előzmény: [1287] lorantfy, 2006-06-21 14:26:28

[1287] lorantfy

2006-06-21 14:26:28

Kedves Jónás és Sirpi!

Kösz a megoldásokat! A 232-est kilőttétek. Végülis, ha valaki rátalál a 7 $\pi$ -re az már jó megoldás, de jobb a lánctörtes, én meg a skatulyásra gondoltam.

Előzmény: [1286] Sirpi, 2006-06-21 12:56:20

[1286] Sirpi

2006-06-21 12:56:20

A 232.-t lehet számolás nélkül is:

Osszuk fel a [0,1)-et 100 db 1/100 hosszú (balról zárt, jobbról nyílt) intervallumra, és jelöljük be rajta a k $\pi$ törtrészeit (k=1..100). Ha az első intervallumba esik elem, akkor készen vagyunk, ha nem, akkor valamelyikbe esik kettő: k₁ $\pi$ és k₂ $\pi$ . Viszont ekkor |k₁-k₂| $\pi$ 1/100-nál közelebb van egy egész számhoz.

Előzmény: [1284] jonas, 2006-06-21 12:24:22

[1285] jonas

2006-06-21 12:32:05

Amúgy az egysorost szinte szó szerint fel lehet olvasni:

+/	Hány olyan dolog van, aminek
*./"1	minden
2v\"1	két szomszédos része
ahol v =. <:/	helyesen rendezett,
(6$10)#:	ha hat tizes számrendszerbeli számjegyre bontjuk
i.1e6	a számokat egymillióig?

Előzmény: [1284] jonas, 2006-06-21 12:24:22

[1284] jonas

2006-06-21 12:24:22

232. feladatra: 7 $\pi$ =21.9911. Egyébként ez az egyetlen. Lánctörtté bontásból is megkapható (3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532 stb az első közelítések), de úgy is, hogy mind a százat végigpróbáljuk.

234. feladatra: Nem lövöm le a számokat, de a 31-es osztási maradékuk 24 (a szigorúan monoton esetben), ill 14 (a monoton esetben). Szintén meg lehet oldani okosan, vagy végigpróbálgatással.

Az ilyen próbálgatásokra, mint az előző kettő, elég hasznos a J programozási nyelv. Komoly programok írására nekem nem alkalmas, de az ilyen egyszerű matematikai számításokat sokkal könnyebben el lehet vele végezni, mint bármilyen más számológép jellegű interpreterrel. A 234. feladatot is két sorban meg lehet vele oldani. A megoldásom (MIME-Base64-enkódolva, mivel ebbe a fórumba nem lehet rendesen kódot beírni):

Ky8qLi8iMV0yPC9cIjEoNiQxMCkjOmkuMWU2CisvKi4vIjFdMjw6L1wiMSg2

JDEwKSM6aS4xZTY=

Ennek a kikódolását kell beilleszteni az interaktív interpreterbe, hogy megkapjuk a két eredményt.

Előzmény: [1283] lorantfy, 2006-06-21 09:41:24

[1283] lorantfy

2006-06-21 09:41:24

232. feladat: Bbh. a $\pi$ ,2 $\pi$ ,3 $\pi$ ...100 $\pi$ számok között van olyan, amely egy egész számtól 0,01-nál kevesebbel tér el!

233. feladat: Bbh. minden n poz. egész számhoz létezik olyan k poz. egész szám, hogy az nk szorzat tízes számrendszerbeli alakja csak 1-es és 0 számjegyeket tartalmaz!

234. feladat: Hány olyan tízes számrendszerbeli hatjegyű szám van melynek számjegyei balról jobbra haladva,

a) szig. mon. növekednek?

b) mon. mövekednek?

Már regisztráltál?
Új vendég vagy?