| [1341] Suhanc | 2006-09-02 20:27:03 |
 Egy lehetséges megoldás Attila feladatára:
(elnézést,ábrát nem tudok mellékelni; egyben kérdezem is, milyen módon készíthetek a későbbiekben megfelelőe kis helyet foglaló ábrát ide?)
A feladat jelöléseit használva, forgassuk el a négyzetet a benne lévő P ponttal együtt B körüli pozitív irányban 90° kal. Ekkor A=C' és nyilván AP=AP'=1, BP=BP'=2 és CP=CP'=3.
A forgatás értelmében PBP'szög= 90° ; mivel BP=BP',így PBP' háromszög egyenlő szárú, derékszögű háromszög, tehát P'PB szög= 45° és 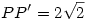 . .
Ekkor APP' háromszögben AP2+PP'2=AP'2=9, tehát a háromszög derékszögű.
A fentiek értelmében APBszög= APP' szög + P'PB szög= 45°+90°=135°.
|
| Előzmény: [1332] jenei.attila, 2006-08-31 11:06:58 |
|
|
| [1339] Sirpi | 2006-09-02 06:38:33 |
 Remélem nem keserítek el senkit, de legjobb tudomásom szerint ez a mai napig megoldatlan. Azt hiszem az volt A jelű Kömal-feladat, hogy az oldalegyeneseken (tehát nemcsak az oldalszakaszokon) nem létezhet ilyen pont.
|
| Előzmény: [1334] Cckek, 2006-08-31 12:10:19 |
|
|
|
|
| [1335] Hajba Károly | 2006-09-01 08:35:50 |
 Üdv! Csak 'hangos' gondolkodás. :o)
Ha a két koordinátaérték nevezőjének szorzatával megszorzom a számlálókat, akkor egész számot kapok, tehát innentől maradhatunk az egész számok között. Tekintsük a pitagoraszi számhármasokat. Ha jól emlékszem, akkor a (m>n>1) N+ esetén az (m2+n2,m2-n2,2mn) számhármas pitagoraszi. E számhármas halmazból kellene tudnom kiválasztani négyet úgy, hogy a 2. és 3. tagjaikat a szükséges módon össze lehessen párosítani. Vagy bizonyítani, hogy ez nem lehetséges. (Ha nem tévedek. :o) N+ esetén az (m2+n2,m2-n2,2mn) számhármas pitagoraszi. E számhármas halmazból kellene tudnom kiválasztani négyet úgy, hogy a 2. és 3. tagjaikat a szükséges módon össze lehessen párosítani. Vagy bizonyítani, hogy ez nem lehetséges. (Ha nem tévedek. :o)
|
| Előzmény: [1334] Cckek, 2006-08-31 12:10:19 |
|
| [1334] Cckek | 2006-08-31 12:10:19 |
 Talán valakinek van valamilyen ötlete a következő jólismert problémához: Van-e az egységnégyzet sikjában olyan pont melynek távolságai az egységnégyzet csúcsaitól racionálisak?
|
|
| [1333] Cckek | 2006-08-31 11:55:08 |
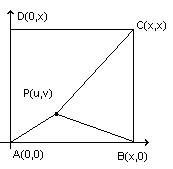
 Vegyük fel az ABCD négyzetet egy koordinátarendszerben, a következő képpen.
Legyenek a P pont kordinátái u, illetve v, és legyen a négyzet oldala x. Ekkor:
PA=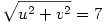
PB=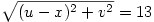
PC=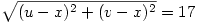
Az egyenletrendszert megoldva az 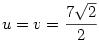 illetve az illetve az 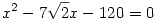 egyenlethez jutunk ahonnan egyenlethez jutunk ahonnan 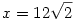 , tehát x2=288 , tehát x2=288
|
 |
| Előzmény: [1329] barnus, 2006-08-31 10:38:47 |
|
|
|
|
|
|
| [1327] Yegreg | 2006-08-30 23:31:02 |
 Azt hiszem 288, de már késő van, szóval feltehetőleg elszámoltam. :)
|
|
| [1326] barnus | 2006-08-30 21:09:57 |
 Köszönöm a megoldást Lorantfy! Itt van egy újabb példa a vállalkozó szelleműeknek! Az ABCD négyzet belseében lévő P pont távolsága három csúcstol sorra PA=7, PB=13 és PC=17. Számítsuk ki a négyzet területét!
|
|
| [1325] rizsesz | 2006-08-29 20:15:37 |
 Hát persze, hogy nem ennyire triviális, hehh. Újabb szórakoztató feladvány 2.0.: A zöldségesnél sorban állnak az emberek, és :) az első, illetve az utolsó ember kivételével :) mindenki azt észrevételezi, hogy az előtte és mögötte álló emberek közül ugyanannyit ismer. Bizonyítsuk be, hogy az első és az utolsó embernek ugyanannyi ismerőse van.
|
|
| [1324] Csimby | 2006-08-29 20:01:33 |
 Mivel az első ember előtt nem áll senki, ezért senkit sem ismer maga előtt, de ugyanannyit ismer maga előtt mint maga mögött, tehát senkit sem ismer. Ugyanígy az utolsó ember mögött sem áll senki, tehát nem ismer maga mögött senkit, tehát maga előtt sem ismer senkit. Vagyis az első és utolsó ember egyaránt nem ismer senkit. De ekkor a második ember senkit nem ismer maga előtt és az utolsó előtti ember senkit nem ismer maga után, tehát Ők sem ismernek senkit sem. Így tovább, senki sem ismer senkit... :-)
|
| Előzmény: [1323] rizsesz, 2006-08-29 19:29:43 |
|
| [1323] rizsesz | 2006-08-29 19:29:43 |
 Egy újabb szórakoztató feladvány:
A zöldségesnél sorban állnak az emberek, és mindenki azt észrevételezi, hogy az előtte és mögötte álló emberek közül ugyanannyit ismer. Bizonyítsuk be, hogy az első és az utolsó embernek ugyanannyi ismerőse van.
|
|
| [1322] lorantfy | 2006-08-28 17:31:59 |
 Szia Barnus!
A feladatot szerintem úgy kell értelmezni, hogy a kocsi minden kereke azonos minőségű, csakhogy az előre szerelt kerekek 24 ezer, a hátulra szereltek 16 ezer km-t bírnak ki a különböző igénybevétel miatt. Mondjuk azért, mert ez a kocsi éppen hátsó kerék meghajtású.
Legyen a gumikon lévő réteg, ami lekophat 1 egység. Ekkor ezer km használat során az első kerékről 1/24, a hátsóról pedig 1/16 egység kopik le.
Használjuk x ezer km-ig a gumikat úgy ahogy fel vannak rakva, majd cseréljük fel az elöl és hátul lévő gumikat és használjuk még y ezer km-ig, úgy hogy mindegyikról lekopjon az egységnyi réteg. Tehát éppen elhasználódnak.
Az először elöl lévő gumik kopása: (1/24)x+(1/16)y=1
A először hátul lévőké: (1/16)x+(1/24)y=1
Közös nevező, összead után: 5(x+y)=96, vagyis max x+y= 19,2 ezer km-t mehetünk a gumikkal.
Hogy mikor kell cseréni, azt találd ki Te!
|
| Előzmény: [1321] barnus, 2006-08-27 16:36:18 |
|
| [1321] barnus | 2006-08-27 16:36:18 |
 Sziasztok!
Van egy érdekes feladatom! A gépkocsira új gumikat szereltek. A hátsó gumik 16000 km megtételére alkalmasak, az elsők 24000 km-re. Mekkora maximális utat lehet megtenni ezekkel a gumikkal? Ha valaki tudja, legyen szíves írja!
|
|
| [1320] Cckek | 2006-08-26 11:26:50 |
 Ha már lehet feladatokat kitűzni akkor itt van néhány saját szerkesztésű feladatom az aritmetika köréből: 1)Határozzuk meg az m,n nullától különböző természetes számokat melyekre fennáll:
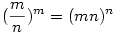
2)Oldjuk meg az
(x+y)m=(xy)n
egyenletet, ahol x,y,m,n N N
3)Oldjuk meg az
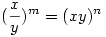
egyenletet, ahol x,y,m,n N* N*
|
|
| [1319] rizsesz | 2006-08-23 22:05:36 |
 rendben :) de néha én is hadd legyek gyors és meggondolatlan :)
|
|
|
|







 N+
N+ 




