| [1925] nadorp | 2007-02-26 21:39:15 |
 Szia Cckek !
Kicsit gyorsan reagáltál :-), de azért egy heurisztikát én is vázolnék ( nem bizonyítás, de szerintem befejezhető, a Te megoldásod viszont teljesen korrekt)
Legyen 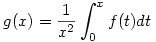 (x>0). Ekkor (x>0). Ekkor
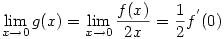 . Tehát . Tehát
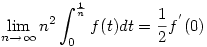 . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege. . A kérdéses szumma éppen a balodalnak egy integrálközelítő összege.
|
| Előzmény: [1923] Cckek, 2007-02-26 20:25:22 |
|
|
|
| [1922] jenei.attila | 2007-02-26 20:16:10 |
 Ákos ne haragudj, de ez teljesen értelmetlen amit írsz. Próbáld meg légyszíves világosabban megfogalmazni. Pl. Mi az n, mi köze a reciprok összegnek az az ai-khez rendelt valós számokhoz (talán az ai-k maguk [a,b] intervallumbeli valós számok? Egyáltalán mik az ai-k)és mit jelent a "jelölje az n-hez tartozó intervallumok számát  (n)" mondat? (n)" mondat?
|
| Előzmény: [1918] S.Ákos, 2007-02-25 19:24:35 |
|
|
|
|
|
|
|
| [1915] Cckek | 2007-02-24 10:29:37 |
 Az 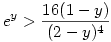 egyenlőtlenség igazolása: Legyen egyenlőtlenség igazolása: Legyen
f:(0,1) R, f(y)=y-ln (1-y)+4ln (2-y). R, f(y)=y-ln (1-y)+4ln (2-y).
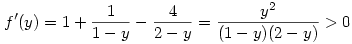 , tehát a függvény szigoruan nő, így , tehát a függvény szigoruan nő, így
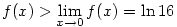 , tehát , tehát
y-ln (1-y)+4ln (2-y)>ln 16 az-az
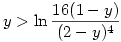 . .
|
| Előzmény: [1911] Cckek, 2007-02-22 21:43:46 |
|
|
| [1913] Lóczi Lajos | 2007-02-23 11:46:57 |
 Jól ismert a binomiális sorfejésbo"l, hogy vannak olyan c1,c2 pozitív állandók, hogy minden, elég kis abszolút értéku" x esetén fennáll az
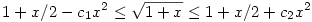
egyenlo"tlenség; egyébként pl. c1=c2=1 megfelelo" az |x| 1 halmazon. 1 halmazon.
Ebbo"l a közrefogási elvvel és az
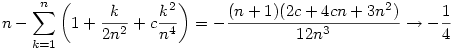
(n  ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4. ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4.
|
| Előzmény: [1908] Cckek, 2007-02-22 15:09:59 |
|
|
|
|
| [1909] Lóczi Lajos | 2007-02-22 19:41:12 |
 Valaki azt állította, hogy a
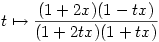
függvény (t-szerinti) határozott integrálja 0 és 1 között minden pozitív x esetén kisebb 1-nél. Igaza van-e neki?
|
|
|
|
|
| [1904] tim20 | 2007-02-22 07:16:52 |
 Egy furcsa fa első nap 1,1/2-szeresére nőtt. Másnap az előző nap 1,1/3-szorosára, harmadnap az előző nap 1,1/4-szeresére és így tovább. Hány nap alatt nőtt meg az eredeti magasságának 100-szorosára?
|
|
| [1903] Cckek | 2007-02-19 19:35:39 |
 Nagyon szép. Gratulálok.
|
|
| [1902] Lóczi Lajos | 2007-02-19 11:30:24 |
 A kerdeses yn sorozat konvergens:
lathato, hogy minden indexre 0<xn<1. Ezt es a rekurziv definiciot hasznalva adodik, hogy
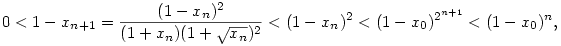
s igy n 1 eseten 1 eseten
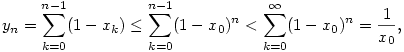
vagyis yn monoton no es felulrol korlatos.
A feladat kituzesehez a motivaciot nyilvan a (gyokvonasra szolgalo) Newton-iteracio adta, hiszen a megadott rekurzio nagyon hasonlit hozza, es a konvergenciasebesseg is olyan ("a helyes tizedesjegyek szama minden lepesben megduplazodik").
|
| Előzmény: [1896] Cckek, 2007-02-16 08:26:44 |
|
|
|




 (n)" mondat?
(n)" mondat?


 Z+ és a
Z+ és a b. Tudjuk, hogy ha az a1;a2;...;an számokhoz 1-1 [a;b]-ben levő valós számot rendelünk, akkor
b. Tudjuk, hogy ha az a1;a2;...;an számokhoz 1-1 [a;b]-ben levő valós számot rendelünk, akkor  R folytonos, 0-ban differenciálható függvény, f(0)=0, akkor
R folytonos, 0-ban differenciálható függvény, f(0)=0, akkor  ) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4.
) határértéket felhasználva adódik, hogy a keresett limesz értéke -1/4. 
 1 eseten
1 eseten