| [2075] Lóczi Lajos | 2007-05-27 16:25:45 |
 Sőt, a Newton-Leibniz-formula alapján minden olyan f folytonos függvény jó lesz, amelynek F primitív függvényére fennáll, hogy 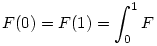 , én ebből a geometrikusabb feltételből találtam meg a , én ebből a geometrikusabb feltételből találtam meg a
f(x):=(x(x-1/2)(x-1))'=3x2-3x+1/2
példát.
|
| Előzmény: [2074] Cckek, 2007-05-27 15:44:29 |
|
|
| [2073] Lóczi Lajos | 2007-05-27 14:17:02 |
 Az eredeti f.) pont kérdésének megválaszolásához expliciten számoljuk ki az U operátor n-edik kompozícióhatványát, ami most könnyen megtehető: legyen x X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván 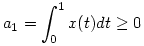 , , 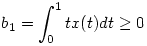 . Az U definíciójából ekkor adódik (hasonlóan ahhoz, amit már szintén láttunk az előző hozzászólásban), hogy . Az U definíciójából ekkor adódik (hasonlóan ahhoz, amit már szintén láttunk az előző hozzászólásban), hogy
an+1=an/2+bn és bn+1=an/3+bn/2.
Ennek a rekurziónak a megoldása
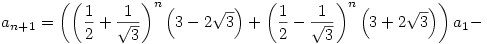
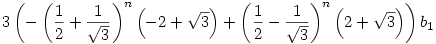
és
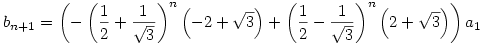
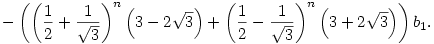
Ebből látszik, hogy tetszőleges s [0,1]-re [0,1]-re ![\lim_{n\to \infty} \root n \of {U^{[n]}(x)(s)}=1/2+1/\sqrt{3}](keplet.cgi?k=01F802F7975E68D1) , ahol az eredmény tehát egy kontans függvény [0,1]-en. , ahol az eredmény tehát egy kontans függvény [0,1]-en.
|
| Előzmény: [2072] Lóczi Lajos, 2007-05-27 13:32:17 |
|
| [2072] Lóczi Lajos | 2007-05-27 13:32:17 |
 Tudjuk, hogy a megadott X tér Banach-tér. Az U operátor nyilván lineáris.
a.) Az U operátor korlátos az X téren és ||U||op. operátornormája éppen 3/2, hiszen az X tér egységgömbjéről vett tetszőleges x függvénnyel
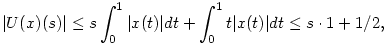
ennek a kifejezésnek a maximuma pedig s [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. [0,1] esetén 3/2, amiből kapjuk, hogy ||U||op. 3/2. Viszont az x(t) 3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető. 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
b.) Mivel tetszőleges x X függvény esetén U(x) egy s X függvény esetén U(x) egy s a.s+b alakú X-beli függvény ( a.s+b alakú X-beli függvény (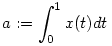 és és 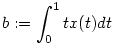 ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor. ), ezért az U operátor ranU értékkészlete részhalmaza az elsőfokú polinomok alterének X-ben, ami véges dimenziós. U tehát véges rangú, emiatt kompakt operátor.
e.) Bármely kompakt operátorra igaz, hogy spektruma csak a sajátértékeiből, illetve legfeljebb a 0 számból állhat. Mivel az X tér most végtelen dimenziós, ismert, hogy a 0 ilyenkor mindig spektrumpont. Megmutatjuk, hogy U-nak csak két nemnulla sajátértéke van.
Ehhez az U(f)= f egyenlet megoldása szükséges: keresendő az összes olyan komplex f egyenlet megoldása szükséges: keresendő az összes olyan komplex   0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely 0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely   0 számok esetén van nemtriviális megoldása az 0 számok esetén van nemtriviális megoldása az
a/3+b/2= b b
a/2+b= a a
egyenletrendszernek. Egyszerűen látszik, hogy ez csak 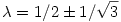 esetén van így, ezek tehát az U operátor nemnulla sajátértékei. esetén van így, ezek tehát az U operátor nemnulla sajátértékei.
U spektruma tehát 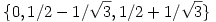 . .
c.) U nem injektív, mert a 0 egyúttal sajátérték is.
d.) A legkevésbé nyilvánvaló állítás a feladatból az, hogy a 0 szám sajátértéke is U-nak. Ehhez olyan f:[0,1] R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis 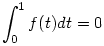 és és 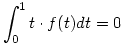 . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek. . Ilyet lehet találni, de kíváncsi vagyok, ki milyen példát ad, a végén erre visszatérek.
f.) A kérdés nem a szokásos alakú, de arra nagyon hasonlít: a kitűző véletlenül itt nem a spektrálsugárra gondolt? Az U operátor spektrálsugara nem más, mint a 0-tól legmesszebb lévő pont a kompakt spektrumból, ami jelen esetben 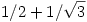 . Ismert, hogy ez a szám egyenlő a . Ismert, hogy ez a szám egyenlő a 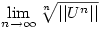 limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.) limesszel -- nem elírás az f.) pont és erre gondoltál? (Az eredeti kérdésre egy lineáris rekurzió megoldása után úgy tűnik, könnyen lehetne válaszolni, de azt még nem néztem meg.)
g.) Jelölje Id az X tér identitásoperátorát. A válasz igen, hiszen az (U-1.Id) operátor (az X X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.) X korlátos lineáris operátorok Banach-terében) invertálható, lévén az 1 nem spektrumpont. (Sőt, emiatt több is igaz: fennáll a kezdeti feltételtől való folytonos függés is.)
h.) Az 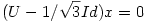 egyenletnek csak az x azonosan 0 függvény a megoldása, mert egyenletnek csak az x azonosan 0 függvény a megoldása, mert 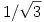 nem spektrumpont, innentől pedig l. az előbbi pontot. nem spektrumpont, innentől pedig l. az előbbi pontot.
Végül visszatérve a fent említett kérdésre, oldjuk meg az alábbi feladatot:
Adjunk példát olyan f:[0,1] R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal R folytonos függvényre, ami nem azonosan nulla, de tetszőleges elsőfokú p polinommal 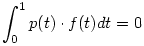 . .
|
| Előzmény: [2071] Cckek, 2007-05-16 22:22:36 |
|
| [2071] Cckek | 2007-05-16 22:22:36 |
 Legyen ![X=(C_{[0,1]},||\cdot||), ||x||=max_{t\in [0,1]}|x(t)|](keplet.cgi?k=CDF0BF029ADA9405) és és ![U:X\to X, U(x)(s)=\int_0^1{(s+t)x(t)}dt, s\in[0,1].](keplet.cgi?k=A9E0891BCE80CFA5)
Számítsuk ki illetve döntsük el a következő kijelentések igaz vagy hamis voltát:
a) ||U||=?
b) U kompakt
c) U injektiv
d) 0 sajátértéke U-nak
e) U spektruma=?
f) 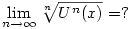
g) x-U(x)=y egyenletnek mindig van egy es csakis egy gyöke, bármely lenne y C[0,1] C[0,1]
h) A 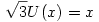 egyenletnek van 0-tól különböző gyöke egyenletnek van 0-tól különböző gyöke
|
|
|
|
| [2068] BohnerGéza | 2007-05-09 00:12:34 |
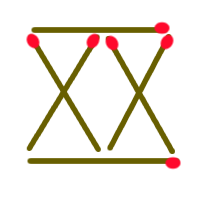
 Mutassuk meg, hogy tetszőleges n pozitív egészre van n db pithagóraszi számhármas, melyekben az átfogó (vagy az egyik befogó) megegyezik!
|
|
|
|
|
| [2064] Gubbubu | 2007-05-08 15:46:12 |
 A negyedik egyértelműen egy halászbárka, amelyet egy 200 méter magas hullám épp a csúcsára vett. A másik három vízijármű egy 200 méter oldalhosszúságú egyenlőszárú háromszög három csúcsát alkotja, melyek mindegyike 200 méter távolságra van a halászbárkától.
A "tengeralattjáró" kifogásolható megoldás, mivel nem a szó szoros értelmében a "tengeren" halad, hanem a tenger>ben< (kivéve persze, ha épp felszíni üzemmódban halad. De akkor meg nem a szó szoros értelmében vett tengeralattjáró, hanem tengeralattjáró, amelyet halászbárkának használnak).
Ez az egzakt megoldás.
|
| Előzmény: [2051] Fálesz Mihály, 2007-05-04 10:47:19 |
|
| [2063] Cckek | 2007-05-06 18:29:46 |
 324.feladat Határozzuk meg azon n-edrendű permutációk számát melyekre |p(i)-i| i i
|
|
|
|
| [2060] Lóczi Lajos | 2007-05-05 01:03:05 |
 Pár kérdés, amit nem értek:
1. Miért lenne log j=j /4 ? Szerintem nem az. /4 ? Szerintem nem az.
2. Valósban sem a kitevő, hanem az alap logaritmusát vesszük egy hatvány definíciójakor, tehát nem jó formulából indulsz ki.
3. exp(k /4) értéke nem k. /4) értéke nem k.
|
| Előzmény: [2059] jonas, 2007-05-04 22:53:31 |
|
| [2059] jonas | 2007-05-04 22:53:31 |
 Jó kérdés.
Azt ugye tudjuk, hogy log j=j /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4, így azt mondhatnánk, hogy ij=exp(ilog j)=exp(ij /4)=exp(k /4)=exp(k /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány. /4)=k. Viszont ugyanígy mondhatnánk, hogy ij=exp(log j.i)=-k. Nem tudom, melyik a helyes, és egyáltalán azt sem, hogy értelmezve van-e a hatvány.
Az előző e alapú hatvány azért volt értelmezve, mert egy valós együtthatós hatványsorba bármilyen kvaternió elemet (vagy mátrixot) be tudunk helyettesíteni, hiszen egy elem hatványai felcserélhetőek egymással és a komplex számokkal is. Ezzel szemben az ix már nem valós, hanem komplex együtthatós hatványsor, amibe pedig nem helyettesíthetünk be akármilyen kvaterniót. Ha j-t az előzőhez hasonlóan egy 4x4-es valós mátrixként fogjuk fel, és behelyettesítjük a komplex hatványsorba, akkor egy nem valós komplex mátrixot kapunk, amit nem foghatunk fel kvaternióként.
|
| Előzmény: [2050] Lóczi Lajos, 2007-05-03 22:15:57 |
|
|
| [2057] Yegreg | 2007-05-04 16:24:05 |
 Igazoljuk, hogy ha x1,x2,...,xn pozitív számok, akkor 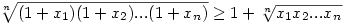 ! !
|
|
|
|
| [2054] HoA | 2007-05-04 13:48:37 |
 Attól még nem hibás egy feladat, hogy több megoldása van. Ha a kitűző azt szeretné, hogy csak egy legyen, szigorítsa a feltételeket. Tehát a 324. feladatra rímelő kitűzés: Hogyan lehet 6 gyufaszálból 4 olyan szabályos háromszöget kirakni, melyek oldala egy gyufaszál hosszú ?
|
| Előzmény: [2053] jonas, 2007-05-04 13:25:40 |
|
|
|
| [2051] Fálesz Mihály | 2007-05-04 10:47:19 |
 324. feladat. Négy hajó halad a tengeren, bármelyik kettő távolsága pontosan 200 méter. Az egyik egy motorcsónak, a második egy jacht, a harmadik vitorlás hajó. Milyen hajó a negyedik?
|
|




 x
x X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván
X rögzített elem, ekkor, ahogyan láttuk, bármely n pozitív egész esetén U[n](x)(s)=ans+bn alakú függvény, alkalmas an és bn számegyütthatókkal. Nyilván  3/2. Viszont az x(t)
3/2. Viszont az x(t) 1 választás mutatja, hogy ||U(x)||=3/2 elérhető.
1 választás mutatja, hogy ||U(x)||=3/2 elérhető.  a.s+b alakú X-beli függvény (
a.s+b alakú X-beli függvény ( f egyenlet megoldása szükséges: keresendő az összes olyan komplex
f egyenlet megoldása szükséges: keresendő az összes olyan komplex  0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely
0 szám és f nem azonosan nulla folytonos függvény X-ből, amelyre a fenti egyenlőség fennáll. Azonban a bal oldal legfeljebb elsőfokú polinom, ahogyan azt láttuk, f(t) kereshető tehát f(t)=at+b alakban (a, b számok). Mivel ekkor U(f)(s)=s(a/2+b)+(a/3+b/2), ezért a sajátérték-egyenlet megoldása ekvivalens a következő kérdéssel: mely  R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis
R folytonos függvényt kell keresni, ami nem azonosan nulla, mégis