| [2200] Csimby | 2007-08-04 15:26:15 |
 n=3k+2 esetén zn+z+1=(1+z+z2)(1-z2+z3-z5+...+zn-2) ahol a jobb oldal második tényezőjében váltakozó előjellel szerepelnek z növekvő hatványai és azok maradnak ki amelyekben a kitevő 3k+1 alakú. Mivel 1+z+z2-nek a 3. primitív egységgyökök gyökei és ezek 1 abszolútértékűek, ezért az egyik irány kész van.
|
| Előzmény: [2198] Csimby, 2007-08-04 15:09:43 |
|
|
|
| [2197] Cckek | 2007-08-04 12:53:25 |
 Egy olimpiászfeladat:
Bizonyítsuk be, hogy a zn+z+1=0 egyenletnek akkor és csakis akkor van egységnyi moduluszú komplex gyöke, ha n 3-mal való osztási maradéka 2.
|
|
| [2196] Hajba Károly | 2007-08-02 08:04:16 |
 OK. Akkor teljes szigorral csak n=7-re ismerünk megoldást.
Alacsony n-re szerintem nincs, ha van, akkor az magasabb n-re lesz. Ez minimum n>7, mivel n=7-re vért izzadva leltünk megoldást.
|
| Előzmény: [2194] Csimby, 2007-08-02 00:56:23 |
|
| [2195] Lóczi Lajos | 2007-08-02 02:14:23 |
 A számítógépbe csak beírom, hogy DSolve, lásd pl. itt.
Amúgy meg a legyegyszerűbb módszer a következő. (Nem írok se vektort, se mátrixot.)
Adott tehát az y'=y+2z és z'=-y+3z rendszer. Kifejezed pl. az elsőből z-t y-nal és beírod a másodikba. Kapsz egy valós, homogén, lineáris, másodrendű egyenletet y-ban. A karakterisztikus polinom két gyöke  1,2=2 1,2=2 i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az 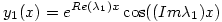 és és 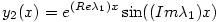 . Emiatt y(x)=c1.y1(x)+c2.y2(x). Innen z(x) már csak egy szimpla visszahelyettesítés. (Láthatod, hogy nem betű szerint ugyanaz jött ki, mint amit a gép adott, de könnyen látszik, hogy c1 és c2-t alkalmasan átnevezve mégsem kaptunk mást.) . Emiatt y(x)=c1.y1(x)+c2.y2(x). Innen z(x) már csak egy szimpla visszahelyettesítés. (Láthatod, hogy nem betű szerint ugyanaz jött ki, mint amit a gép adott, de könnyen látszik, hogy c1 és c2-t alkalmasan átnevezve mégsem kaptunk mást.)
|
| Előzmény: [2193] Willy, 2007-08-02 00:35:58 |
|
|
| [2193] Willy | 2007-08-02 00:35:58 |
 Megkérhetnélek mindkettőtöket, hogy mutassátok meg, ti egész pontosan hogyan oldanátok meg a feladatot (a gépesnek is nagyon örülnék). (Ugyanis se diffegyenletet nagyon, se komplex függvénytant nem tanultam még suliban, csak saját szakállamra; és nem nagyon látom át a helyzetet.)
Előre is köszönöm :-)
|
| Előzmény: [2192] Lóczi Lajos, 2007-08-02 00:20:51 |
|
|
| [2191] Cckek | 2007-08-01 21:26:43 |
 Bocs Willy, az előző hozzászolásomban a mátrix:
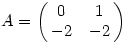 . .
Elfelejtettem, hogy megváltoztattam a feladat adatait:)
|
|
| [2190] Cckek | 2007-08-01 21:19:55 |
 Helló Willy.
Igen, valami ilyesmi jött ki nekem is vizsgán, bár kissé bonyolultabban. 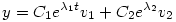
Ahol  1=-1+i, 1=-1+i, 2=-1-i sajátértékek és 2=-1-i sajátértékek és
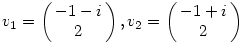 sajátvektorok. Na ezt kéne valóssá alakítani. sajátvektorok. Na ezt kéne valóssá alakítani.
|
| Előzmény: [2186] Willy, 2007-08-01 02:36:51 |
|
| [2189] Hajba Károly | 2007-08-01 21:14:07 |
 De ez ugye csak nem-kilépő? Mert nálam a visszazárt annyit tesz, hogy a kiindulási pontba zár vissza. Azaz nem lehet a gráf egyetlen pontja sem páratlan élű, csak páros. Nálam. :o)
Ha a bal alsóból [1,1] indulsz, akkor csak a [4,4]-be érkezhetsz. Erre én is ráleltem, csak én nem hosszabbítottam meg a már meglévő vonalig. Az [1,1]-be kellene vissza is érkezni.
|
| Előzmény: [2188] Csimby, 2007-08-01 20:36:28 |
|
|
|
| [2186] Willy | 2007-08-01 02:36:51 |
 Szia Cckek!
Nem vagyok valami penge a diffegyenltekből, de megnéztem egy próbafüggvényre:
Legyen
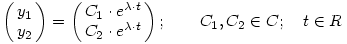
(Érzésem szerint ez a próbafüggvény minden megoldást vissza fog adni.)
Végezzük el a mátrixszorzást és a próbafüggvény deriválását is:
![\left(\matrix{y_1\cr y_2\cr}\right)'= \left( \matrix{C_1\cdot \lambda \cdot e^{\lambda\cdot t}\cr C_2\cdot \lambda \cdot e^{\lambda\cdot t}\cr} \right)= \left[\matrix{1&2\cr -1&3\cr}\right]\cdot \left( \matrix{C_1\cdot e^{\lambda\cdot t}\cr C_2\cdot e^{\lambda\cdot t}\cr} \right)= \left(\matrix{(C_1+2C_2)\cdot e^{\lambda\cdot t}\cr (-C_1+3C_2)\cdot e^{\lambda\cdot t}\cr}\right)](keplet.cgi?k=1B896813E872F5CC)
Ebből kapunk egy három paraméterrel rendelkező, egyváltozós, két egyenletből álló egyenletrendszert:
C1. =C1+2C2 =C1+2C2
C2. =-C1+3C2 =-C1+3C2
Elsőből kifejezzük C2-t, beírva a másodikba és rendezve, kapjuk:
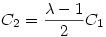
0=C1.( 2-4. 2-4. +5) +5)
1) Ezek alapján C1=C2=0 és   R azaz R azaz 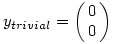
2) Avagy,  1,2=2 1,2=2 i, C1 i, C1 R és R és 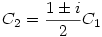 , azaz , azaz
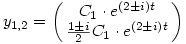
A három megoldás...
|
| Előzmény: [2183] Cckek, 2007-07-29 20:18:25 |
|
|
|
| [2183] Cckek | 2007-07-29 20:18:25 |
 Adott az 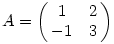 . Oldjuk meg az y'=Ay differenciálegyenletet. . Oldjuk meg az y'=Ay differenciálegyenletet.
|
|
|
| [2181] epsilon | 2007-07-29 14:01:01 |
 Helló Cckek, a Te szimpatikus feladatodra akartam választ adni, de egy sorral lennebb klickeltem, így a Doom nickre hívatkozik a válasz!
|
|
| [2180] epsilon | 2007-07-29 13:58:09 |
 Helló! Ha jól számoltam akkor a tört abszolútértéke 1/3, nem de? Pl. végezzük el a z=3+z' transzformációt, így a feltétel alapján abs(z')=1 ezért jelölje z"=konjugált(z). Így 1/z'=z" továbbá ha az abs[(4-z)/(4+z)]=E akkor E=abs[(3z'+1)/(3z'+9)]=1/3*A ahol A=abs[(3z'+1)/(z'+3)]. Most a tört számlálóját és nevezőjét is tagonkénz osztva z'-tel, a konjugálás tulajdonsága alapján azt kapjuk, hogy A=1/A adódik, és A>0 tehát A=1, így E=1/3.
|
| Előzmény: [2177] Doom, 2007-07-28 19:57:48 |
|
| [2179] epsilon | 2007-07-29 13:10:22 |
 Kösz Doom! Az még vettem észre, azzal valóban jobban be lehet osztani csoportokra, de valójában azt a keresési módszereket hiányolom, amikor konkrét szóra, stb. lehetne rákeresni, de gondolom, hogy ezt nem könnyű megvalósítani, mert már megtették volna, nem Én találnám fel a spanyolviaszt! Üdv: epsilon
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
|
| [2177] Doom | 2007-07-28 19:57:48 |
 A hozzászólások felett jobb felül: hány hsz legyen a lapon és rendezze a legöregebbel kezdve... innen már te is ki tudod egyszerűen számolni, hogy melyik sorszám hányas lapra esik... ;)
Ha olyan gyorsabb keresésre gondoltál, ami kulcsszavak alapján működne, az szerintem is hasznos lenne.
|
| Előzmény: [2176] epsilon, 2007-07-28 19:35:48 |
|
| [2176] epsilon | 2007-07-28 19:35:48 |
 Kedves Károly! Hát így sorszámszerint valahogy könnyebb volt betájolni, de tényleg kár, ha nem létezik olyan keresés, hogy ha beírod az adott hsz számát, akkor oda vigyen...de hát meglehet, hogy csak Nekem hiányzik. Mindenképpen kösz a segítséget! Üdv: epsilon
|
|






 1,2=2
1,2=2 i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az
i, vagyis (használva az Euler-formulát) két lineárisan független megoldás az 
 R azaz
R azaz 
