|
| [2239] Sirpi | 2007-08-23 21:56:59 |
 Azt, hogy a fv. hol vesz fel racionális értékeket, szerintem se érdemes túlzottan vizsgálni. Annyi bizonyos, hogy a folytonosság miatt a minimuma és maximuma között felveszi az összeset.
Már az x3-x fv.-ről se látom kapásból, hogy milyen irracionális értékekra racionális (ehhez az x3-x-p/q=0 harmadfokú egyenletet kell megoldani mindenféle p,q értékekre).
|
| Előzmény: [2226] Cckek, 2007-08-22 12:21:54 |
|
| [2238] Csimby | 2007-08-23 21:48:33 |
 Szerintem, ha ennyire lemegyünk, az alapokig, hogy 1>0, akkor tisztáznunk kell a definíciókat, hogy tudjuk mit használhatunk a bizonyítás során. Nem gondoltam utána, de nem vagyok benne biztos, hogy pl. CCkek bizonyítása nem használja-e fel valahol, hogy 1>0.
|
| Előzmény: [2236] Lóczi Lajos, 2007-08-23 18:31:13 |
|
|
| [2236] Lóczi Lajos | 2007-08-23 18:31:13 |
 A teljességre valóban nincs szükség.
A felvetésednek mindazonáltal nem igazán látom értelmét: legyen összesen 2 elemünk, és egy ">"-gyel jelölt reláció. Az egyetlen igaz állítás (axióma) a rendszerünkben pedig legyen az, hogy "1>0". A jelek jelentését firtatni itt értelmetlen. :)
|
| Előzmény: [2235] HoA, 2007-08-23 17:00:28 |
|
| [2235] HoA | 2007-08-23 17:00:28 |
 Úgy látom, Gyöngyő nem érti, mennyire jogos Csimby felvetése. Szerintem a feladatot valahogy úgy kéne megfogalmazni: Mi az a minimális fogalom, definíció, axióma halmaz, amiből adódik, mit jelent a "0", az "1" és a ">" , és amiből be lehet bizonyítani az állítást? Úgy sejtem, a teljesen rendezett kommutatív test fogalmára nincs szükség.
|
| Előzmény: [2232] Gyöngyő, 2007-08-23 12:30:27 |
|
| [2234] Cckek | 2007-08-23 14:12:01 |
 Most épp Csebisev polinomokkal foglalkozgatom, tahát Tn(x)=cos (narccosx) polinom. Mi a helyzet forditva? arccos(ncos x) hogyan néz ki? Vagy általánosan melyek azok a bijektív függvények melyekre
f(n.f-1(x)) polinom?
|
|
|
|
|
|
|
|
| [2227] Gyöngyő | 2007-08-22 17:49:19 |
 Sziasztok!
Lenne egy olyan kérdésem,hogy hogyan lehet bebízonyítani,hogy 1>0 (egy nagyobb mint nulla)?
Köszönettel:
Gyöngyő
|
|
|
|
| [2224] Lóczi Lajos | 2007-08-22 12:07:23 |
 Gondolom, x valós. Ekkor elegendő a [0,2 ] intervallumot nézni. Mivel [ ] intervallumot nézni. Mivel [ ,2 ,2 ]-n a szinusz negatív és negatív alap esetén nehézkes a valós számok körében hatványokat értelmezni, ezért ezt a részt most hagyjuk ki. Marad a [0, ]-n a szinusz negatív és negatív alap esetén nehézkes a valós számok körében hatványokat értelmezni, ezért ezt a részt most hagyjuk ki. Marad a [0, ] intervallum. A koszinusz negatív ezen intervallum jobb felén. Marad [0, ] intervallum. A koszinusz negatív ezen intervallum jobb felén. Marad [0, /2]. Itt viszont az eredeti függvény tengelyesen szimmetrikus e legutóbbi intervallum felezőmerőlegesére, tehát elég [0, /2]. Itt viszont az eredeti függvény tengelyesen szimmetrikus e legutóbbi intervallum felezőmerőlegesére, tehát elég [0, /4]-re szorítkozni. /4]-re szorítkozni.
Az eredeti bal oldal x=0-ban éppen 1. De minden x (0, (0, /4)-re (sin x)cos x+(cos x)sin x>1, hiszen /4)-re (sin x)cos x+(cos x)sin x>1, hiszen
(sin x)cos x+(cos x)sin x (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon. (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon.
Azt is könnyű meggondolni, hogy (sin x)cos x+(cos x)sin x sosem lehet 2, hiszen 0 és 1 közötti számok 0 és 1 közé eső hatványa ugyanilyen, de egyszerre nem lehet mindkettő 1.
Ezekből az eredeti kérdésre a válasz már rögtön kiolvasható, ha nem tévedtem sehol.
|
| Előzmény: [2223] Cckek, 2007-08-22 10:13:55 |
|
| [2223] Cckek | 2007-08-22 10:13:55 |
 Oldjuk meg a (sin (x))cos (x)+(cos (x))sin (x)=k Z egyenletet:D Z egyenletet:D
|
|
|
| [2221] Cckek | 2007-08-10 17:43:13 |
 Köszi szépen Lajos a tanulmányokat, nagyon érdekesek, az említett azonosságra tudok egy indukciós bizonyítást, mely elég hosszú, ezért lettem volna kiváncsi más ötletekre...
|
| Előzmény: [2220] Lóczi Lajos, 2007-08-09 23:36:02 |
|
|
|
| [2218] Cckek | 2007-08-08 12:09:35 |
 Gyönyörűszép levezetés, gratula. Azt hiszem, hogy Cesaro-Stolzzal is megy, mármint ha nem csesztem el valahol:)
Első Stolz után 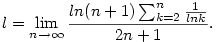
Második Stolz után: 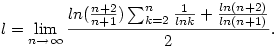
Már csak azt kell felhasználni, hogy 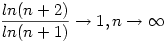 és és 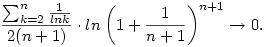
|
| Előzmény: [2217] nadorp, 2007-08-08 00:22:25 |
|
| [2217] nadorp | 2007-08-08 00:22:25 |
 Ennek nem lehet ellenállni :-) ( Remélem jó is lesz a megoldás)
Egy jelölés: Ha {an},{bn} két sorozat, akkor an bn jelölje az asszimptotikus egyenlőséget, tehát hogy bn jelölje az asszimptotikus egyenlőséget, tehát hogy 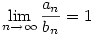 . Felhasználtam a következőket: . Felhasználtam a következőket:
a.) 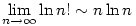
b.) Ha {an},{bn} két pozitív sorozat, és an bn valamint bn valamint 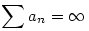 , akkor , akkor 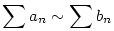
A feladatban szereplő összeg az alábbiak szerint is írható
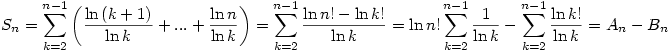
Belátjuk, hogy 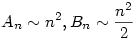 ,innen már következik ,innen már következik 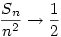
1.) 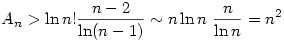
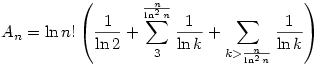
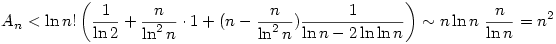
2.) Mivel 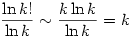 , ezért , ezért
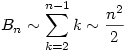
|
| Előzmény: [2213] Lóczi Lajos, 2007-08-07 00:22:27 |
|
|









 /4 speciális esetben adódó
/4 speciális esetben adódó  Q?
Q?  (sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon.
(sin x)1+(cos x)1, ez utóbbi függvény viselkedése pedig egyszerű: tudjuk, hogy >1 a megadott intervallumon.  (3) irracionális" állításról is szól.
(3) irracionális" állításról is szól.
 bn jelölje az asszimptotikus egyenlőséget, tehát hogy
bn jelölje az asszimptotikus egyenlőséget, tehát hogy