| [223] Hajba Károly | 2004-01-17 01:11:18 |
 50. feladat:
Adott két kanóc, melyek egyenként pontosan 1-1 óra alatt égnek le, de az égési sebességük véletlenszerűen változó. (Tehát a fele nem feltétlen fél óra alatt ég le.)
Hogyan tudunk ezen kanócok segítségével 0,75 órát lemérni?
51. feladat:
Hogyan lehet egy szál kolbászt 10-nél kevesebb vágással úgy feldarabolni, hogy akár 3, akár 4 egyenlő részre lehessen osztani?
52. feladat:
Hogyan lehet egy négyzet alakú tortát 3 egyenes vágással felszeletelni, hogy akár 3, akár 4 egyenlő részre lehessen osztani?
HK
|
|
| [222] Gubbubu | 2004-01-16 18:32:09 |
 Kedves Onogur!
Semmi baj, úgy sejtettem, hogy az eredeti szövegrészben egy rész véletlenül törlődött (ilyesmi sokszor előfordul, kétszer át szoktam nézni, mit írok, de mindig kerül hiba bele). Az első féle általánosítás így is érthető volt. Persze, megoldani egyiket sem tudom, a numerikus és közelítő módszerek elmélete nemigen megy nekem.
Üdv.: G.
(U.I. Azt hiszem, megoldottam a mágusos feladatot, de még várok egy-két hétig, mielőtt felteszem, hátha más is szeretne még gondolkodni.)
|
| Előzmény: [221] Hajba Károly, 2004-01-16 14:07:52 |
|
| [221] Hajba Károly | 2004-01-16 14:07:52 |
 Kedves gubbubu!
A kétféle általánosítási irány összevonását elkapkodtam. Tehát korrigálva magam:
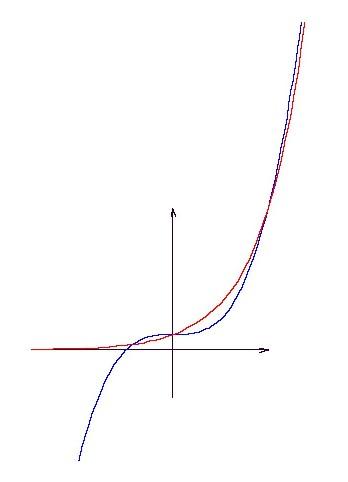
1. A x2+d=2x egyenlet görbéinek jellegéből adódik, hogy 1, 2 v. 3 megoldás lehetséges, ahol d lehet 0 értékű is, továbbá mely d-re adódik 2 megoldás?
2. A feladaton lehet általánosabban is az an+d=na formában gondolkodni. Pl. x3+1=3x esetet az ábra mutatja. (y harmadával torzítva és ott fenn van még egy metszéspont.) x1 -0,845838;x2=0;x3=2;x4 -0,845838;x2=0;x3=2;x4 3,220644. Így itt 4 metszéspont van. 3,220644. Így itt 4 metszéspont van.
Remélem, most már nem írtam marhaságokat. :o)
HK
|
 |
| Előzmény: [220] Gubbubu, 2004-01-16 00:46:54 |
|
| [220] Gubbubu | 2004-01-16 00:46:54 |
 Üdv, Onogur,
Kösz a kimerítő (de érdekes) magyarázatot, és a történeti kiegészítést! Most már lesz min gondolkodnom a következő kb. 5 évben... Valószínűleg már az sem triviálisan látható be, hogy mindig lf. 3 metszéspont van, mert a "görbék jellege" kifejezés arra utal, hogy minimum differenciálszámítás van a háttérben. Legalábbis ilyentájt, 0:36-kor egyelőre ennyit vagyok képes látni.
Persze ki lehet tűzni a "Nehezebb matematikai problémák" rovatban ezeket az általánosításokat... hátha egyszer valaki megoldja őket... mondjuk valaki, aki "lovaszlaszlo" n.name-mel van bejelentkezve...
Üdv: G.
|
| Előzmény: [219] Hajba Károly, 2004-01-15 09:24:06 |
|
| [219] Hajba Károly | 2004-01-15 09:24:06 |
 Kedves gubbubu!
- A Bezier-görbék és a továbbfejlesztett változatuk a B-spline módszer 30 éve kezdett el terjedni a mérnöki számítógépes formatervezés területén. Lényege, hogy adott pontokkal leírjuk a görbét vagy térbeli felületet és a pontok közötti vonalat ill. felületet súlyozott paraméterfüggvénnyel írjuk le. Lényeges, hogy a pontokban és illeszkedési vonalakban legalább másodrendűen illeszkednek a görbék ill. felületek. A pontokkal, s illeszkedésükkel lehet globális vagy lokálisan változtatni ill. a súlyozás mértékét is lehet szabályozni a modell megjelenésén.
P. Bezier a '70-es évek legelején dolgozta ki e módszert a Renault gépkocsik formatervezésének számítógépes modellezése során, s ezt vették át más mérnöki területek is.
- A felvetetted problémán egyébként már korábban én is gondolkodtam a x2=2x formában. Ennek is két egészértékű megoldása van. Továbbá felvetésed után a következő általánosítások vetődtek fel bennem:
A görbék jellegéből adódik, hogy 1, 2 v. 3 megoldás lehetséges, s általában na+d=an alakú, ahol d lehet 0 értékű is, továbbá a és d függvényében mely d-re adódik 2 megoldás?
HK
|
| Előzmény: [218] Gubbubu, 2004-01-15 00:58:00 |
|
| [218] Gubbubu | 2004-01-15 00:58:00 |
 Kedves Onogur!
Hűha! A Bezier-görbét nem ismerem, de a neve nem hangzik rosszul, ahogy az sem, amit az egész CAD-os eljárásról mondtál. Nem hittem volna, hogy egy ilyen, viszonylag egyszerű alakú (bár nem feltétlenül egyszerűen megoldható) egyenlet ábrázolása mögött is komoly matematika húzódhat meg. Hiába, nekem az alkalmazott matematika tudásom nem jár a fellegekben!
Ami a pótkérdéseket illeti: természetesen nem várom, hogy örökké csak az én kérdéseimre válaszolj, nagyon köszönöm az eddigi hozzászólásaidat is... csak automatikusan fölvetődtek, mint a megoldásból természetesen következő problémák.
Egyébként eme példa hatására a következő sejtés fogalmazódik meg az emberben: ahogy 4-nél magasabb fokú polinomiális egyenletek megoldására nincs gyökképlet, úgy az f(x)=xk egyenletek (f(x) k-adfokú polinom) sem oldhatóak meg alapműveletek, 2..k-adik gyökvonás és (mondjkuk k alapú) logaritmuskeresés segítségével... Úgyhogy jöhetnek a mérnökök, hajrá közelítő számítások... Soha nem hallottam, hogy ilyen témájú, azaz exponenciális-polinomiális kevert egyenletek képlettel való megoldására irányuló kutatások folytak volna valahol (bár mintha halványan emlékeznék, hogy a differenciálegyenletek elméletében van valami szerepük az ilyen egyenleteknek), de ha valaki tud valamit róluk, csak szóljon.
Viszlát mindenkinek holnap: G.
|
| Előzmény: [217] Hajba Károly, 2004-01-15 00:06:40 |
|
| [217] Hajba Károly | 2004-01-15 00:06:40 |
 Kedves Gubbubu!
A rajzolást nem egyszerűbb, de rajzprogrammal készítettem. Mérnök lévén, rendelkezésemre áll egy profi CAD program, de innentől kezdve "csaltam", mint Rodolfo. Minden egészértékhez kiszámoltam a függvényértéket és erre a koordinátahelyre pontot illesztettem, majd a pontsorra egy Bezier-görgét. A parabolát százalékos, míg a hiperbolát ezrelékes pontossággal követi. A harmadik metszéspontot 2 tizedesjegy pontossággal megadta, innen már numerikusan finomítottam az értéket.
A pótkérdéseidre nem tudok válaszolni, mivel a szakmámhoz nem szükséges matematikatudásom nem jár a fellegekben. Talán Géza vagy Sirpi mondanak valami érdekeset e témáról. :o)
HK
|
| Előzmény: [214] Gubbubu, 2004-01-14 20:09:39 |
|
| [216] Gubbubu | 2004-01-14 23:50:07 |
 Kedves Csimby;
Valóban, ez nem tűnik borzasztó nehéznek. Sőt, alighanem a 2n+1=n2 diofantikus egyenlet is hasonlóképp oldható meg. Vagyis 23 az egyetlen kettőhatvány, melyhez egyet adva a hatvány (az alap és kitevő szerepe) "megfordul".
Köszönettel: G.
|
| Előzmény: [215] Csimby, 2004-01-14 22:27:23 |
|
| [215] Csimby | 2004-01-14 22:27:23 |
 Az egészek könnyen megmondhatóak: Ha n nagyobb/egyenlő kettővel, akkor (2 az n.-en), 4-gyel mindig osztható, míg n*n+1, 4-gyel osztva 1 vagy 2 maradékot ad -> marad az n=0 és n=1 eset.
|
|
| [214] Gubbubu | 2004-01-14 20:09:39 |
 Kedves Onogur, azaz Károly!
Köszönöm a megoldást, külön az ábrát. Érdekelne, hogy mivel csináltad (pl. valamilyen mat. szoftverrel, vagy egyszerűbb rajzprigrammal)? Én szabadkézi rajzzal próbálkoztam, de - amint látható - a két görbe túlságosan összeesik, így eltekintve a két triviális megoldástól és a harmadik szemmel láthatótól, nemigen látszott semmi.
Ezek után már csak két kérdés marad:
48.B. feladat: Nem lehetne valahogy algebrailag vagy számelméletileg megoldani? Megelégednék azzal is, ha csak az egész megoldásokat találnánk meg, de számolással.
48.C. feladat: Nincs-e a harmadik, nem egész megoldásnak pontos értéke, mondjuk valami egész szám logaritmusa?
Emlékeztetőül: a n2+1=2n egyenletről van szó.
|
| Előzmény: [213] Hajba Károly, 2004-01-14 13:13:16 |
|
| [213] Hajba Károly | 2004-01-14 13:13:16 |
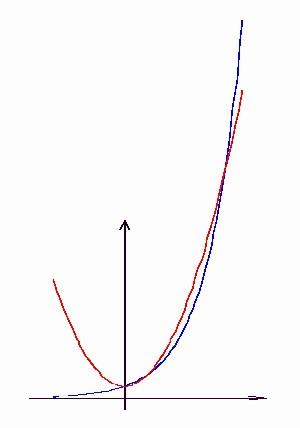
 Kedves gubbubu!
A 48. feladatra itt van az ábra, ott lent kétszer metszik egymást a görbék. Továbbá a három megoldásból két nyilvánvaló eredmény az x1=0 ill. x2=1, továbbá az általam közelítő módszerrel kiszámolt x3 4,25746. 4,25746.
|
 |
| Előzmény: [207] Gubbubu, 2004-01-06 21:14:24 |
|
| [212] Kós Géza | 2004-01-11 15:11:06 |
 A diszkrét fogalma megengedi hogy a halmaznak legyen torlódási pontja, csak a torlódási pont nem lehet a halmazban. Például az 1,1/2,1/3,... sorozat diszkrét, pedig van torlódási pontja, a 0.
Mindkét értelmezésben igaz, hogy Rn-ben minden diszkrét halmaz megszámlálható, ezt többféleképpen is be lehet bizonyítani. Nem írom le egyik megoldást sem, csak útbaigazítást szeretnék adni.
1. megoldás: A halmaz minden pontjához rendeljünk hozzá (valahogy, ügyesen) egy olyan, közeli pontot, aminek mindegyik koordinátája racionális.
2. megoldás: Osszuk fel a teret megszámlálható sok korlátos részre, például egységkockákra, és keressünk olyan kockát, amiben a halmaznak sok pontja van.
Akinek esetleg mindez túl könnyű, annak egy nehezebb változat: Bizonyítsuk be, hogy egy f:R R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x >0 szám, hogy minden x (a- (a- ,a+ ,a+ ), x ), x a esetén f(x)<f(a).) a esetén f(x)<f(a).)
|
| Előzmény: [211] Csizmadia Gábor, 2004-01-10 16:50:46 |
|
| [211] Csizmadia Gábor | 2004-01-10 16:50:46 |
 49. feladat
Szerintem nagyon érdekes ez a feladat, már régóta foglalkoztatott a kérdés, de csak nemrég tudtam megadni rá a választ: Ismeretes, hogy bizonyos ponthalmazok diszkrét pontokból állnak, bizonyos ponthalmazok pedig nem. Diszkrét ponthalmazoknak nincs torlódási pontjuk. Ha a természetes számokat ábrázoljuk a számegyenesen, akkor azok diszkrét pontokként jelennek meg. A racionális számok számossága megegyezik a természetes számokéval, a számegyenesen mégis minden pontjuk torlódási pont. Valós számokat úgy képzeljük el, hogy folytonosan kitöltik a rendelkezésre álló számegyenest, valamint tudjuk, hogy a valós számok számossága nagyobb, mint a természetes számoké. Általában egy euklideszi tér pontjai ugyanannyian vannak, mint a valós számok. De vajon létezik-e olyan diszkrét Rn-beli (n természetes szám, tehát egyenes pontjaiból álló, síkbeli, térbeli, vagy magasabb dimenzióbeli) ponthalmaz, aminek ugyanannyi pontja van, mint ahány valós szám?
|
|
|
|
| [208] Csimby | 2004-01-07 00:07:28 |
 Legyen a számtani sorozat 1. eleme: a, differenciája d, ekkor az első n+1 elem összege: a+(a+d)+(a+2d)+(a+3d)+...+(a+nd)=(n+1)a+(n(n+1)/2)d=(n+1)(a+(n/2)d). T.F.H. ez egyenlő a szorzatukkal: (n+1)(a+(n/2)d)= a(a+d)(a+2d)(a+3d)...(a+nd) Osszunk le (a+(n/2)d)-vel: (ha n páratlan akkor ez nem szerepel a jobb oldalon,de végig lehet gondolni, hogy így is jó). n+1=a(a+d)(a+2d)...(a+(n/2-1)d)(a+(n/2+1)d)...(a+nd) ha d=0, akkor trivi, nézzük most d>1-et, ekkor: a+nd>a+n. a=0 trivi. Ha a>=1 akkor a+n>=n+1 -> a+nd>n+1, és mivel a szorzatban minden tag >=1, a szorzat nagyobb lesz a bal oldalon maradt (n+1)-nél (hiszen a jobb oldalon szerepel (a+nd) mint szorzó tényező) Maradt a d=1 eset. a+nd=a+n,csak akkor ha a szorzásban a többi tényező 1 -> n=2, a=1
|
|
| [207] Gubbubu | 2004-01-06 21:14:24 |
 Üdv!
Rövid időre megint itt vagyok.
Örülök, hogy legalább egyik feladatom megoldhatónak (tehát értelmesnek) bizonyult, remélem szereztem egy kellemes percet GJ-nek, nem hiszem, hogy tovább törte volna a fejét... köszönet a frappáns megoldásért!
Valahol a http://orange.ngszkij.hu honlapon állítólag van néhány megjegyzés e feladattal ill. általánosításaival kapcsolatban (nekem hibát jelez a Netscapem, ha odamegyek, nem tudom, pontosan hol).
Néhány hiba vagy hiányosság került az előző, 204-es hozzászólásomba (csak most tanulom a TEX-et...):
1. a második 47. feladat valójában a 48. (feltéve, ha az előzőek számozása hibamentes);
2. Eme feladatnak elsősorban az algebrai-számelméleti jellegű megoldásai érdekelnének, bár ha valaki ábrát készítene, az is szép lenne... (A feladatban az lenne az "érdekes", hogy egy hatványhoz egyet adva fordul az alap és a kitevő szerepe, jé!...)
3. A 6-ról szóló feladatban cáfolással érdemes próbálkozni, legalábbis valós számokból álló számtani sorozatok esetében. Ha a kérdéses számtani sorozat tagjai-elemei számát 2-re ill. 3-ra korlátozzuk, "kellemes" kis polinomgyök-keresési ill. diofantikus problémákat kapunk, nem muszáj rögtön az egész feladatot teljesen általánosan megoldani...
Megjegyzem, nyithatnánk egy Érdekes matematikai feladatok II. topicot az eddig megoldatlan feladatokat összegyűjtendő, mert kezd a dolog áttekinthetetlenné válni...
|
|
| [206] lorantfy | 2004-01-06 20:50:09 |
 Kedves Attila!
Kösz a helyreigazítást. Én is rájöttem a hibára, csak már azután, hogy feltettem a hozzászólást. Hirtelen valami olyasmire gondoltam, hogy miközben x mint valós szám végigfut az adott intervallumon, a zárójelben lévő kifejezés értékei milyen egész számokat érintenek, és ezek szummája. Ez persze hülyeség, elkapkodtam!
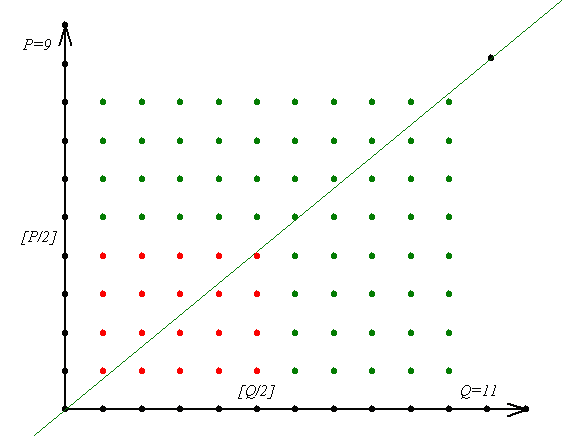
Nagyon szép és szemléletes a megoldásod! Az a fajta, amit megnéz az ember és csak fogja a fejét: - Milyen egyszerű, mért nem jutott ez nekem eszembe? Felteszek egy ábrát, hátha más is kedvet kap, hogy megnézze a hozzá tartozó feladatot és megoldást! (Lászlónak hívnak!)
|
 |
| Előzmény: [203] jenei.attila, 2004-01-05 15:27:03 |
|
| [1452] jenei.attila | 2004-01-06 10:55:56 |
 Sziasztok!
A 41.feladat megoldása
A feltételekből következik, hogy p|ab+ac+ad+ae+bc+bd+be+cd+ce+de -nek. A szimmetrikus polinomok alaptétele szerint mindem szimmetrikus polinom előáll elemi szimmetrikus polinomok polinomjaként. Ez alapján:
a5+b5+c5+d5+e5=5abcde+(a+b+c+d+e)5-
-5(a+b+c+d+e)3(ab+ac+bc+ad+bd+cd+ae+be+ce+de)+5(a+b+c+d+e)(ab+ac+bc+ad+bd+cd+ae+be+ce+de)2+
+5(a+b+c+d+e)2(abc+abd+acd+bcd+abe+ace+bce+ade+bde+cde)-
-5(ab+ac+bc+ad+bd+cd+ae+be+ce+de)(abc+abd+acd+bcd+abe+ace+bce+ade+bde+cde)-
-5(a+b+c+d+e)(abcd+abce+abde+acde+bcde)
. Innen már látszik a feladat állítása.
|
| Előzmény: [182] Pach Péter Pál, 2003-12-08 20:18:19 |
|
| [205] GJ | 2004-01-05 19:35:20 |
 46.feladat p prím,tehát 3-mal osztva 1 vagy 2 maradékot ad tehát ha p maradéka 1 (3-mal osztva)->p+2 maradéka (3-mal osztva) 0->p+2 nem prím hasonlóan ha p maradéka 3-mal osztva 2,akkor p-2 maradéka 0(3-mal soztva)->p-2 nem prím
vagyis nincs az 5-ön kívül ilyen p prím
|
| Előzmény: [204] Gubbubu, 2004-01-05 19:22:37 |
|
| [204] Gubbubu | 2004-01-05 19:22:37 |
 Üdvözlök mindenkit!
A két ünnep között egy nap azzal szórakoztam, hogy a természetes számok során valameddig végigmenve a számokat különféle nevezetes sorozatokba soroltam. Ennek során egész érdekes, könnyebb-nehezebb problémákra bukkantam, sokat egyáltalán nem tudok vagy nincs időm megoldani, de hátha másokat érdekel. Néhány példa:
46. feladat:
Van-e olyan p prím az 5-ön kívül, amelyre p-2, p és p+2 is prím? Keressünk minél többet, vagy lássuk be hogy nincs.
47. feladat:
Lássuk be vagy cáfoljuk meg, hogy 6 az egyetlen szám (poz. egész, egész, rac., valós vagy komplex), amely ugyanazon számtani sorozat elemeinek egyszerre az összege és a szorzata!
47. feladat:
Oldjuk meg a n2+1=2n egyenletet!
Egyenlőre ennyi.
(Várhatóan hétvégén jövök újra, addig megoldani!)
|
|
| [203] jenei.attila | 2004-01-05 15:27:03 |
 Kedves István!
A Te megoldásoddal az a baj, hogy miközben az x végigmegy a megfelelő egész számokon, nem biztos, hogy 1-től egyesével növekedve kapjuk a számokat [P/Q*x]-ből, hanem a sorozatban az egymás utáni tagok [P/Q]-val, vagy [P/Q]+1 -gyel növekszenek.
Vegyük a derékszögű koordináta rendszerben a P/Q meredekségű, origón áthaladó egyenest, és tekintsük az x=1, y=1, és x=[Q/2], y=[P/2] egyenesek által határolt téglalapot. Ekkor a bizonyítandó egyenlőség mindkét oldala, a téglalapban található rácspontok (mindkét koordinátája egész) számát adja (a határokat is beleértve). Ugyanis [P/Q*x] az x-en áthaladó függőleges egyenesen fekvő, P/Q meredekségű egyenes alatti, a szóbanforgó téglalapba eső rácspontok száma. Ha x végigfut a megfelelő egész számokon, nyilván megkapjuk az összes, téglalapba eső, P/Q meredekségű egyenes alatti rácspontok számát. A másik szumma ugyanígy az egyenes feletti rácspontok számát adja. A feltételek biztosítják, hogy nem esik rácspont a P/Q meredekségű egyenesre, így minden pontot csak egyszer számolunk. Márészt a jobboldali kifejezés közvetlenül a téglalapban fekvő rácspontok számát adja.
|
| Előzmény: [194] lorantfy, 2003-12-17 23:58:40 |
|
|
|
|




 -0,845838;x2=0;x3=2;x4
-0,845838;x2=0;x3=2;x4



 R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan
R függvénynek csak megszámlálható sok helyen lehet szigorú lokális maximuma. (Egy a pontban szigorú lokális maximuma van, ha létezik olyan  >0 szám, hogy minden x
>0 szám, hogy minden x (a-
(a- a esetén f(x)<f(a).)
a esetén f(x)<f(a).)