| [2476] HoA | 2007-12-05 11:11:43 |
 Nem is tudom, most örüljek-e, hogy sikerült rájönni egy megoldásra, amihez valóban elég egy 8 éves tudása. Az ebben a megoldásban felhasznált tulajdonság felismeréséhez nem a 10 négyszög léte, hanem az segít, ami hiányzik az ábráról :-)
|
| Előzmény: [2474] rizsesz, 2007-12-04 14:05:10 |
|
|
|
| [2473] Hajba Károly | 2007-12-04 14:01:11 |
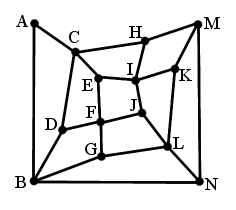
 A vonalak 10 db négyszöget határoznak meg. Ha ezeket átalakítjuk egy újabb gráffá úgy, hogy a négyzetek a gráfcsúcsok és a csatlakozó él az új gráf élei, akkor ebben a gráfban is meg kellene tudni csinálni az összekötést. Ha nem sikerül, akkor az eredetiben sem lehet.
Persze tudom ez nem bizonyítás. Inkább csak morfondíroztam egyet. :o)
|
| Előzmény: [2471] Csimby, 2007-12-04 12:47:51 |
|
| [2472] rizsesz | 2007-12-04 13:58:02 |
 Akkor gondolj arra, hogy a hivatalos megoldás tulajdonosa 2. osztályos volt. És nem középiskolás, hanem általános iskolás, azaz 8 éves. Szóval érdemes elrugaszkodni egy kicsit attól, amit az ember tud, és olyan fejjel gondolkodni, mintha csak nagyon alapvető eszközeink lennének. :)
|
| Előzmény: [2470] Hajba Károly, 2007-12-04 12:38:43 |
|
| [2471] Csimby | 2007-12-04 12:47:51 |
 Szerintem is egy szép feladat :-) Ha alég sokáig nézi az ember a gráfot, akkor észre lehet venni valamit ami nagyon sokat segít.
|
|
| [2470] Hajba Károly | 2007-12-04 12:38:43 |
 Elvileg ez egy nyílt Hamilton-kör lenne, amire nincs egyértelmű megoldhatósági kritérium, mint az Euler-körre van. Nekem úgy tűnik, nem létezik Hemilton-kör, de a gráfok mélységében nem vagyok eléggé járatos, így nem tudom bizonyítani.
|
| Előzmény: [2467] Csimby, 2007-12-04 01:26:25 |
|
|
|
|
| [2466] Csimby | 2007-12-04 01:19:45 |
 Láttam most egy hasonlót (legalábbis annyiban hasonlít, hogy körmérkőzéses :-):
330.feladat 8-an körmérkőzést játszanak (nincs döntetlen). Biz.be, hogy mindig kiválasztható 4 olyan versenyző, akik közül az első legyőzte a másodikat, harmadikat és negyediket, a második legyőzte a harmadikat és negyediket, valamint a harmadik legyőzte a negyediket.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
|
| [2464] HoA | 2007-11-27 18:36:33 |
 Egy másik megoldás a 6 versenyzőre: Legyen a(z egyik) győztes A. Mivel összesen 6 x 5 / 2 = 15 pontot osztanak ki (sakk) , neki legalább 2.5 pontja van. Vegyük az A-t tartalmazó párok P halmazát ( 5 pár ) és a P párokat legyőzők G halmazát . G nem lehet 1 elemű, mert akkor saját magát is le kellene győznie. De nem lehet 3 vagy több elemű sem, mert akkor A-t legalább hárman legyőzték volna, tehát nem lehetne csak 5-3 = 2 pontja. Ha viszont G kételemű, akkor G tagjai A-tól 2, a többi 5 résztvevőtől együtt legalább 5 pontot szereztek, így együtt legalább 7 pontjuk van, az egyiknek legalább 3.5. A viszont a 2 pont elvesztésével legfeljebb 3 pontos lehet, ami ellentmond annak, hogy ő a(z egyik) győztes.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
|
| [2462] Enkidu | 2007-11-27 13:23:05 |
 A hétszereplős kőrmérkőzésre a válasz: lehetséges.
A következő táblázat mutat egy lehetséges esetet: az egyes sorokban azt jelöltem, hogy az adott játékost ki verte meg.
1| 2,3,4 (2,3 és 4 veri az 1-est) 2| 3,6,7 3| 4,5,7 4| 2,5,6 5| 1,2,7 6| 1,3,5 7| 1,4,6
A példád továbbgondoltam 7-nél több szereplő esetére.(Nem lesz valami nagy durranás) Szóval ekkor is megoldható, hogy bármely 2-höz legyen aki veri mindkettőt. Pl. az összes többit verje a 2,3,4-es (az első 7-en kívűli összes többit). Ez nyilván megfelelő.
Sziasztok!
|
| Előzmény: [2438] nadorp, 2007-11-23 08:10:45 |
|
|
| [2460] Sirpi | 2007-11-27 11:01:14 |
 Köszi, sokat segítettél :-)
Emiatt a 396 miatt egyrészt leesett az állam, másrészt arra is rájöttem, hogy ennek fényében nem biztos, hogy érdemes túl sok időt belefeccölnöm a probléma vizsgálatába...
Ja, és itt egy példa, amikor páratlan sok elem tölti ki a téglalapot (bár nem minimális), ezt hirtelen találtam, lehet, hogy van kisebb is.
|
| Előzmény: [2459] Hajba Károly, 2007-11-27 01:09:54 |
|
|
|
|
| [2456] Sirpi | 2007-11-26 15:38:24 |
 Igazad van, ez kimaradt. Én úgy vettem, hogy lehet tükrözni. Bár az is érdekes lehet, hogy milyen különbség adódhat egy adott alakzat esetén, ha megengedjük, illetve ha nem engedjük meg a tükrözést.
És igen, én is 10-est találtam még az 1,2,4-en kívül. Vajon van más?
|
| Előzmény: [2454] Hajba Károly, 2007-11-26 14:26:42 |
|
|
|
| [2453] Sirpi | 2007-11-26 12:53:02 |
 Felmerült bennem egy probléma, egyelőre csak ízlelgetem. Az egyszerűség kedvéért nevezzünk rácsidomnak rácsnégyzetekből álló, élek mentén illeszkedő, összefüggő alakzatokat (gondoljatok a tetrisre, de nem feltétlen kell 4 kis négyzetből állnia az alakzatnak). Ezek között vannak olyanok, amiket többször felhasználva ki lehet rakni egy téglalapot, másokból meg nem. Az előbbiekhez rendeljük hozzá az ehhez szükséges minimális darabszámot. Tehát ha az alakzat eleve téglalap, akkor 1-et, a tetrisben pedig pl. az L-alakhoz 2-t, a T-alakhoz 4-et rendelünk.
A kérdés az, hogy mekkora lehet maximálisan ez a szám? Vagy egyáltalán, milyen más értékek adódhatnak így?
Mindenesetre találtam 4-nél nagyobbat már, innen jött az ötlet.
|
|
| [2452] Lóczi Lajos | 2007-11-25 22:46:37 |
 Nem olyan nehéz ez.
Tudjuk, hogy x, y és z pozitívak. Az x g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0. 0, A>0, B>0.
Azt kapjuk, hogy
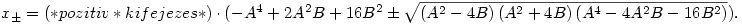
Ki akarjuk zárni, hogy g<0 pozitív x-ekre.
Ha a diszkrimináns negatív, készen vagyunk.
Ha a diszkrimináns A2-4B miatt nulla, szintén készen vagyunk, mert ez annak felel meg, ha y=z, de 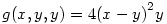 . .
Elég tehát az A4-4A2B-16B2 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív. 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív.
Elemi módon látszik, hogy A4-4A2B-16B2 0 és -A4+2A2B+16B2 0 és -A4+2A2B+16B2 0 és A2-4B 0 és A2-4B 0 egyszerre nem teljesülhetnek a pozitív számpárok körében. 0 egyszerre nem teljesülhetnek a pozitív számpárok körében.
Az kell tehát csak megnézni, mi van, ha -A4+2A2B+16B2 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van. 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|









 C1[0,1] függvényt melyre
C1[0,1] függvényt melyre  ).
).

 g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B
g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0.
0, A>0, B>0.  0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.