| [249] Sirpi | 2004-02-17 13:12:19 |
 Ja, és Csimby, bocs, hogy ugyanazt mondtam el, mint Te, de mivel azt írta itt valaki, hogy még nem oldódott meg a 47. példa, söt, Zormac is írt rá egy megoldást, ezért nem álltam neki utánanézni, hogy tényleg meg lett-e már oldva. Bocsi érte.
S
|
| Előzmény: [245] Csimby, 2004-02-16 20:12:00 |
|
| [248] Sirpi | 2004-02-17 12:45:11 |
 Sziasztok!
Akinek anno tetszett a farkas, kecske, káposzta folyón való átvitele, de túl könnyünek találta, annak itt egy kicsit nehezebb változat:
A nagy japán folyós játék
Sajna a szöveg japánul van, de ez ne riasszon el senkit, a kezdöképernyön a nagy kerek gombra kell bökni, és utána át kell juttatni az anyukát, apukát, két lányukat, két fiukat, valamint a rendört és a fegyencet a túlpartra, a következök figyelembevételével:
- Mindenkinek át kell menni a folyón
- Csak két személy lehet egyszerre a tutajon
- Az apa nem maradhat egyedül egyik lánnyal sem mert megveri ot
- Az anya nem maradhat egyedül egyik fiúval sem mert megveri ot
- A fegyenc (csíkos ruha) nem maradhat a rendor felügyelete nélkül mert megver valakit
- Csak az anya, az apa és a rendor vezetheti a tutajt
- A fegyenc egyedül maradhat, nem fog megszökni
Jó szórakozást a játékhoz!
S
|
|
| [247] Zormac | 2004-02-17 12:28:57 |
 57. feladathoz
Nem tudom, vajon van-e ennek a feladatnak elemi megoldása, s mivel én nem találtam olyat, így programmal estem neki. Ha már lúd, legyen kövér: nem csak a kitűzött formátumú megoldásokat kerestem, hanem másokat is, amelyek ráillenek a kiírás szövegére. Az eredeti, vagyis az AB*CDE=GHIJ formátumból az alábbi hetet találta a progi:
12 x 483 = 5796; 18 x 297 = 5346; 27 x 198 = 5346; 28 x 157 = 4396; 39 x 186 = 7254; 42 x 138 = 5796; 48 x 159 = 7632
Emellett adódott két darab A*BCDE=GHIJ típusú megoldás (4 x 1738 = 6952; 4 x 1963 = 7852), valamint számtalan A*B*CDE=GHIJ és A*BC*DE=GHIJ típusú is, például 3 x 28 x 71 = 5964 illetve 6 x 9 x 138 = 7452.
A négyféle típus elemeinek összlétszáma 79.
Akit esetleg érdekel, a program forrása és teljes kimenete megtalálható itt.
|
| Előzmény: [246] Hajba Károly, 2004-02-16 22:43:09 |
|
| [246] Hajba Károly | 2004-02-16 22:43:09 |
 57. feladat:
Tekintsük a 48×159=7632 szorzatot, melyben az 1-9 számjegyek mindegyike szerepel, de csak egyszer. Képezzünk hasonló szorzásokat!
HK
|
|
| [245] Csimby | 2004-02-16 20:12:00 |
 Én is ezt mondtam [216]-ban, de hát gyorsan felejtenek a népek...
|
|
| [244] Sirpi | 2004-02-16 11:07:28 |
 n2+1=2m és m 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás. 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
m=0 esetén n=0, m=1 esetén n= 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk. 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
S
|
| Előzmény: [238] Zormac, 2004-02-12 16:24:18 |
|
| [242] Lóczi Lajos | 2004-02-13 23:49:10 |
 Kedves Onogur,
ha csak képlet kell, azt könnyű gyártani:) Íme egy, amely megadja az egyenlet megoldását, ha az iteratív módszer már szóba került:
lim(ak),
ahol ak+1=log2(ak2+1), és például a0=4. (A limesz létezik, mert az ak sorozat monoton növő és felülről korlátos.)
|
| Előzmény: [240] Hajba Károly, 2004-02-13 13:27:42 |
|
|
| [240] Hajba Károly | 2004-02-13 13:27:42 |
 Kedves Zormac!
n=4 42+1>24 42+1>24
n=5 52+1<25 52+1<25
Így a (4,5) tartományban van egy megoldás, ezt én iteratív úton meghatároztam [214], továbbá tény, hogy n>5 megoldás már nem létezik, amire hozzászólásodban utaltál. Mi arra is kiváncsiak lettünk volna, hogy ez képlet formájában megadható-e. Eddig erre nem jött válasz, tehát szerintem nem olyan egyszerű a feladat.
HK
|
| Előzmény: [238] Zormac, 2004-02-12 16:24:18 |
|
|
| [238] Zormac | 2004-02-12 16:24:18 |
 A 47. feladat valóban nem kelt el, pedig egyszerű... (az volt, hogy oldjuk meg: n2+1=2n).
Először is n=0 és n=1 megoldások, 2 n n 5 pedig nem megoldások, amint azt könnyű ellenőrizni. Ráadásul n=5-re már igaz, hogy 2n<n2+1 és ennek az öröklődését könnyű belátni nagyobb n-ekre, például azáltal, hogy a 2n sorozat hányados-sorozata nagyobb, mint az n2+1 sorozaté (afféle indukció): 5 pedig nem megoldások, amint azt könnyű ellenőrizni. Ráadásul n=5-re már igaz, hogy 2n<n2+1 és ennek az öröklődését könnyű belátni nagyobb n-ekre, például azáltal, hogy a 2n sorozat hányados-sorozata nagyobb, mint az n2+1 sorozaté (afféle indukció):
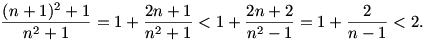
Esetleg az lehetne egy nehezebb feladat, hogy oldjuk meg az alábbit (nem tudom, értelmes feladat-e, csak úgy eszembe jutott, hátha mi lesz :-)
n2+1=2m.
|
|
| [237] lorantfy | 2004-02-12 13:24:38 |
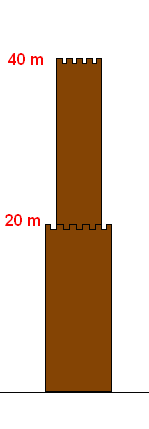
 56.feladat: 40 m magas torony tetejéről kell lejutnunk. Van egy 30 m-es kötelünk, késünk és gyufánk. A kötelet csak 40 m és 20 m magasságban lehet rögzíteni. Leugrani persze semmilyen magasságból sem tanácsos.
(Aki ismeri, ne lője le!)
|
 |
|
| [236] lorantfy | 2004-01-24 17:46:38 |
 A 35. feladat a Cornides István Matematika - Fizika Emlékverseny 1.feladata volt és így szólt:
Határozza meg, mely p valós számokra van az
x3+px2+2px=3p+1
egyenletnek három különböző a, b, c valós gyöke, amelyre ab=c2.
35. faladat megoldása: A három gyök a, b, c tehát a gyöktényezős alak:
(x-a)(x-b)(x-c)=x3-(a+b+c)x2+(ab+ac+bc)x-abc=0
Összehasonlítva ezt az eredeti egyenlettel és alakítgatva:
a+b+c=-p  a+b=-c-p a+b=-c-p
ab+ac+bc=2p  ab+(a+b)c=2p ab+(a+b)c=2p
abc=3p+1 mivel ab=c2  c3=3p+1 c3=3p+1
Második egyenletbe ab és (a+b) értékét beírva:
c2+(-p-c)c=2p  -pc=2p -pc=2p  0=p(c+2) 0=p(c+2)
Tehát p = 0 vagy c=-2
p=0 esetén x3=1 a=1, b=1, c=1 és ab=c2 is teljesül.
Ha c=-2, akkor p = -3, a+b=5, ab=4 és így a2-5a+4=0.
Gyökei: a=1 vagy a=4, amihez b=4 vagy b=1 tartozik.
p= -3 esetén az eredeti egyenlet gyökei valóban 1, 4 és -2.
|
| Előzmény: [233] Hajba Károly, 2004-01-23 11:50:49 |
|
|
| [234] Hajba Károly | 2004-01-23 12:24:42 |
 55. feladat:
Daraboljuk az egységnégyzetet kisebb négyzetekre.
A) Milyen részekre nem lehet feldarabolni?
B) Lehet-e legalább 11 féleképpen feldarabolni 11 részre?
HK
|
|
| [233] Hajba Károly | 2004-01-23 11:50:49 |
 Kedves Topik!
A még meg nem oldott feladatok listája:
3. [3] (félig megoldva!)
12. [60]
35. [148]
40. [180]
44. [199]
47. [204]
54. [229]
Jó gondolkodást a hétvégére :o)
HK
|
|
| [232] Hajba Károly | 2004-01-22 08:21:42 |
 Kedves László!
Tény, hogy hamar lelőttem, de cserében feltettem gyorsan egy másikat. Hasonló feladatokat a GEOMETRIA topikba is raktam, de eddig nem harapot rá senki, pedig lehetne még néhányat feladni. Érdekes - legalábbis számomra - a kitölthetőségi téma.
HK
|
| Előzmény: [229] lorantfy, 2004-01-21 14:32:49 |
|
| [231] Elti | 2004-01-21 17:18:42 |
 Szevasztok, csao! szeretnelek titeket ertesiteni arrol, hogy a trefort.chat.net -en megalakult a KoMaL szoba, szivesen varunk mindenkit, hogy kialakithassunk egy jo kis matekos, fizikas legkort! remelem minnel tobben leszunk! Hello
|
|
| [230] pataki | 2004-01-21 17:00:22 |
 Érdemes megnézni az 1990. évi diákolimpia 3. feladatát.
Ez egyúttal könyvajánlás is: Reiman István - Dobos Sándor: Nemzetközi Matematikai Diákolimpiák 1959 - 2003, Typotex Kiadó
|
| Előzmény: [216] Gubbubu, 2004-01-14 23:50:07 |
|
|
| [228] Hajba Károly | 2004-01-21 14:10:54 |
 Kedves László!
54. feladat:
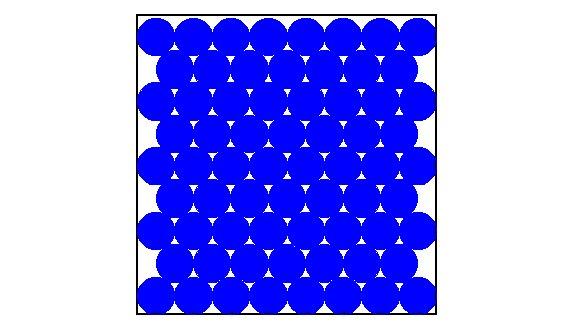
Vegyünk el ebből a 64 golyóból 1 darabot. Mekorra az a legkisebb négyzet alakú keret belső mérete, amibe még bele lehet rakni ezt a 63 darab golyót?
HK
|
| Előzmény: [226] lorantfy, 2004-01-21 13:37:20 |
|
|
| [226] lorantfy | 2004-01-21 13:37:20 |
 53. feladat: Egy 8 egység belső méretű négyzet alakú keretbe belaraktunk 64 db 1 egység átmérőjű fémgolyót. (A golyók egymással és a keret falával érintkeznek)
Hány ugyanilyen golyót tudnál még berakni a keretbe?
|
 |
|
|
| [224] lorantfy | 2004-01-18 21:34:02 |
 Kedves Károly!
Ügyes példák – főleg a gyujtózsinóros!
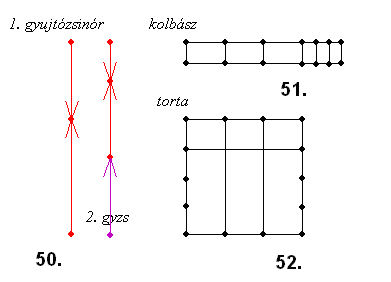
50. feladat megoldása: Elég reménytelennek tűnik a megoldás, mivel véletlenszerűen égnek a zsinórok nem darabolhatjuk őket. Akkor mit lehet tenni? Ami biztos, hogy, ha mondjuk már fél órája ég a zsinór akkor a hátralévő zsinórdarab is fél óráig ég még. Tehát ha mindkét végét meggyujtjuk az egyik zsinórnak, akkor 1/2 óra alatt ér össze a láng.
Ha a másik zsinórt is meggyujtjuk az első két végének meggyujtásával egyidőben, akkor amikor az elsőn a láng összeér a másik zsinórból még pont félórányi van hátra. Ekkor meggyujtjuk a második zsinór másik végét is és a két láng pontosan 1/4 óra múlva ér össze. Tehát lemértük a 3/4 órát.
51. feladat megoldása: A kolbászt 3 vágással felvágjuk 4 egyenlő részre, majd az egyik részt továbi két vágással harmadoljuk.
52. feladat megoldása: A tortát 2 párhuzamos vágással harmadoljuk, majd 1 merőleges vágással elvágjuk az 1/4 részénél.
|
 |
| Előzmény: [223] Hajba Károly, 2004-01-17 01:11:18 |
|






 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.  1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk. 
 42+1>24
42+1>24  n
n

 a+b=-c-p
a+b=-c-p