| [2601] Róbert Gida | 2008-03-16 14:04:28 |
 Triviális. Legyen m=1236789689135*n-206131614856 alakú prím, ismeretes, hogy ezekből végtelen sok van Dirichlet tétele miatt (feltétele teljesül), ilyen prímekre  (6*m)< (6*m)< (6*m+1) lesz, hiszen az elsőt pontosan ki tudod számolni, mert m az prím, a másodikat pedig becsüld alulról, használva azt, hogy ekkor 6*m+1 osztható minden prímmel 5-től 37-ig, így *találtam ki*. Például n=25-re prímet ad, azaz m=30713610613519 megoldás lesz, ezt közvetlenül is ellenőrizheted, ez persze nem biztos, hogy a legkisebb megoldás, hiszen egy más konstrukció is adhat jó m-et. (6*m+1) lesz, hiszen az elsőt pontosan ki tudod számolni, mert m az prím, a másodikat pedig becsüld alulról, használva azt, hogy ekkor 6*m+1 osztható minden prímmel 5-től 37-ig, így *találtam ki*. Például n=25-re prímet ad, azaz m=30713610613519 megoldás lesz, ezt közvetlenül is ellenőrizheted, ez persze nem biztos, hogy a legkisebb megoldás, hiszen egy más konstrukció is adhat jó m-et.
|
| Előzmény: [2599] Gyöngyő, 2008-03-16 13:00:58 |
|
| [2600] S.Ákos | 2008-03-16 13:58:06 |
 Megnézve az [1;1020] intervallumot, eddig nem találtam megoldást, és úgy néz ki, hogy a függvényértékek közötti eltérés nő, egyre nagyobb lesz 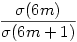 . Többet sajnos még nem tudok mondani. . Többet sajnos még nem tudok mondani.
|
| Előzmény: [2599] Gyöngyő, 2008-03-16 13:00:58 |
|
| [2599] Gyöngyő | 2008-03-16 13:00:58 |
 Sziasztok!
Tudnátok segíteni a következő feladatban:
Keressük a legkisebb pozitiv egész m-et amelyre  (6m)< (6m)< (6m+1)fenntáll. (6m+1)fenntáll.
A másik kérdés pedig,az h mutassuk meg,hogy a fennti egyenlőtlenségnek végtelen sok megoldása van.
Ahol  (m) az osztók összegét jelenti. (m) az osztók összegét jelenti.
Köszönettel
|
|
| [2598] szbela | 2008-03-15 15:13:01 |
 Sziasztok!
Esetleg megnézzük (i) x=0, (ii) x=0 és y=0 esetekre? Bár nem tudom, hogy ez így jó-e.
(i) x=0 : f(x+f(y))=f(0+f(y))=f(f(0))+f(y)
(ii) x=0 és y=0 : f(x+f(y))=f(0+f(0))=f(f(0))=f(f(0))+f(0)
(i)-nek és (ii)-nek teljesülnie kell: (ii)-ből következett, hogy f(f(0))=f(f(0))+f(0), ebből f(0)=0 tehát f(f(0))=0 szintén. Ezt (i)-be helyettesítjük és kapjuk, hogy f(f(y))=f(y) Ennek persze minden y-ra teljesülnie kell. És mivel f: R->R -be képez, ezért ha f(y)=a, akkor f(a)=a f(y)=f(f(y)) miatt. f tehát az identitásfüggvény lenne.
|
| Előzmény: [2595] Gyöngyő, 2008-03-14 20:29:51 |
|
| [2597] Cckek | 2008-03-15 09:56:31 |
 Egy ötlet: f(f(x+f(y)))=f(f2(x)+f(y))=f(f(y)+f2(x))=f(f(f(y)))+f2(x)=f2(f(y))+f2(x). Legyen f(y)=t Imf Imf
Ekkor f2(x+t)=f2(x)+f2(t), tehát az f2 függvény kielégíti Cauchy funkcionálegyenletét az RxImf halmazon.
|
| Előzmény: [2595] Gyöngyő, 2008-03-14 20:29:51 |
|
|
| [2595] Gyöngyő | 2008-03-14 20:29:51 |
 Sziasztok!
Nekem is van egy érdekes feladatom:
Keressük meg az összes R-ből R-be képző nemcsökkenő függvényt amelyre f(x+f(y))=f(f(x))+f(y) fennáll minden valós x és y-ra
|
|
| [2594] kicsipega | 2008-03-10 09:44:52 |
 sziasztok!
Még új vagyok negyon tetszik ez a fórum, bár még nem olvastam égig az összes feladatot és megoldást. A 44. feladatnak van egy kicsit nehezítet változa. A fekete és fehér marhák egy négyzetbe, a tarka és barna marhák egy háromszögbe tudnak felsorakozni.
Ha már volt bocsi az ismétlésért.
Gabi
|
|
|
| [2592] epsilon | 2008-03-09 21:16:09 |
 Ha elvégzed az 1/x=y változócserét, akkor visszakapod a [2589] Cckek integrálját aminek az eredménye éppen [2590] Lóczi Lajos-tól. Nem de?
|
|
|
|
|
| [2588] Róbert Gida | 2008-01-28 00:29:29 |
 Aszimptotikusan 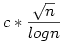 , ahol c>0 konstans, ez is megsejtehő, mint például az ikerprím konstans. , ahol c>0 konstans, ez is megsejtehő, mint például az ikerprím konstans.
Freud Gyarmati régi ELTE számelmélet jegyzetét megnéztem, ott sincs kimondva a sejtés, csak az irreducibilitás és a primitívség, de ez nem elég! n2+n+2 polinom például irred. és primitív, de csak a 2-t veszi fel prímként (minden egész helyen a polinom értéke páros). Szerintem már csak annyit kell feltenni, hogy, ha a polniom foka d, akkor minden p d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá. d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá.
|
| Előzmény: [2587] V Laci, 2008-01-27 22:28:12 |
|
|
| [2586] Róbert Gida | 2008-01-27 19:53:47 |
 Tehát, hogy végtelen sok van-e, az a kérdés? p=2 nem megoldás, egyébként feltehető, hogy p páratlan prím, így a négyzetszám is páratlan, legyen ez (2*n+1)2, ekkor rendezve az kell, hogy p=n2+n+1 alakú prímből végtelen sok legyen, mivel ez irreducibilis és primitív polinom, ezért egy idevonatkozó mély sejtés szerint végtelen sok ilyen prím van (elsőfokúra Dirichlet tétel, nagyobbra nem tudjuk, hogy igaz-e). Sőt ha a számukat kérdezed adott N-ig, hogy hány ilyen p prím van az is megsejthető.
|
| Előzmény: [2585] V Laci, 2008-01-27 19:22:26 |
|
| [2585] V Laci | 2008-01-27 19:22:26 |
 Sziasztok!
Nemrég találkoztam az alábbi érdekes problémával (bár lehet, hogy nehezebb, mint érdekesebb).
Hány olyan p prím van, amelyre 4p-3 négyzetszám?
|
|
|
| [2583] komalboy | 2008-01-26 13:36:58 |
 h lehet azt igazolni, h a két rekurzió ugyanaz?
|
|
|
|
|
|
|
|



 (6*m)<
(6*m)<



 Imf
Imf 
 d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá.
d-re a polinom Fp[x]-ben nem az azonosan nulla polinom. (p>d-re, ha a polinom primitív, akkor a fokszámtétel miatt nem lehet nulla a polinom). Ez persze a te n2+n+1 polinomodat nem érinti, ez is teljesül rá.
 B
B