| [2903] jenei.attila | 2009-04-04 09:08:53 |
 A jó sorozatokat következőképpen számoljuk össze: egy n hosszúságú jó sorozatban az előző n-1 elemből álló sorozat is jó. Jelöljük an-nel a nem fehér színnel végződő n hosszúságú jó sorozatok számát, bn-nel pedig a fehérrel végződők számát. Ekkor a jó sorozatok száma (amit cn-nel fogunk jelölni) nyilván cn=an+bn és a1=4 b1=1.
an=an-1+4bn-1
, mivel nem fehérre végződő jó sorozatot úgy kapunk, hogy az n-1 -edik elem nem fehér és akkor az n-edik elem ugyanolyan színű, vagy az n-1 -edik elem fehér de akkor az n-edik elem 4 féle színű lehet. Hasonlóan meggondolva
bn=an-1+bn-1
a fehérre végződő jó sorozatok száma annak megfelelően, hogy ekkor a megelőző n-1 hosszú jó sorozatot fehér színnel folytatjuk. Egy kis alakítással kapjuk: c1=5, c2=13
cn=2cn-1+3bn-1
(mivel cn=an+bn)
bn=cn-1
,amiből végül
cn=2cn-1+3cn-2
másodrendű lineáris rekurzió adódik. Meglehet adni zárt alakban is, ezt másra hagyom.
|
| Előzmény: [2894] gubanc, 2009-04-01 11:51:00 |
|
| [2902] jonas | 2009-04-02 19:25:54 |
 Ja értem. Én úgy próbáltam színezni a pontokat, hogy bármelyik két szomszédos vagy különböző színű legyen, vagy az egyik fehér. Te viszont azt mondtad, hogy bármelyik két szomszédos pont legyen vagy azonos színű, vagy az egyik közülük fehér.
Ebben az esetben a megfelelő sorozat szerintem az A046717 lesz.
|
| Előzmény: [2898] gubanc, 2009-04-01 20:22:57 |
|
| [2901] gubanc | 2009-04-02 16:27:50 |
 Látom, a legjobb úton haladsz a feladat általánosítása felé (Pl.: 5 szín helyett k szín ...). Csak dícsérni tudom ezt a kezdeményezést! :))
Előre is köszönet mindkettőtöknek, és az esetleges további hozzászólóknak is. (gubanc)
|
| Előzmény: [2900] BohnerGéza, 2009-04-02 15:19:38 |
|
|
| [2899] BohnerGéza | 2009-04-01 22:07:18 |
 Telhetetlen vagy gubanc!
(: Egy és két szín esetén tudnék segíteni. :)
(Sőt, egyelőre azt hiszem, három vagy több szín esetén lényegében ua. a feladat, esetleg a zárt alak megadásában lehetnek különböző nehézségűek. Azért megpróbálom komolyabban is.)
|
| Előzmény: [2894] gubanc, 2009-04-01 11:51:00 |
|
| [2898] gubanc | 2009-04-01 20:22:57 |
 Sajnos még mindig nem világos számomra a dolog. Hogyan érted azt, hogy "el kell tolni eggyel a sorozatot"? Azt láttuk, hogy a sorozat első tagjának 5-nek kell lennie. Ha ehhez igazodunk, akkor az OEIS-ből belinkelt sorozatot kettővel (és nem eggyel) eltolva a1 = 5 és a2 = 21 adódna. Így meg a2-vel van egy kis probléma ... . Egyébként javasolom, hogy lépjünk túl a rekurziós alakon és n  3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét). 3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét).
(Elnézést, ha valamit félreértettem volna.)
|
| Előzmény: [2897] jonas, 2009-04-01 19:00:06 |
|
|
| [2896] gubanc | 2009-04-01 16:06:19 |
 Ha jól látom, az általad megadott hivatkozás a1 = 1 -et ír, ami ellentmond annak, hogy n = 1 esetén az egyetlen pontot - az öt szín miatt - ötféleképpen színezhetjük ki.
|
| Előzmény: [2895] jonas, 2009-04-01 15:28:31 |
|
|
| [2894] gubanc | 2009-04-01 11:51:00 |
 Szép napot! Kíváncsi lennék a köv. feladat megoldására.
Egy egyenesen sorakozik n pont ilyen sorrendben: P1, P2, ... , Pn. Adott öt különböző szín, egyikük a fehér. Kiszíneztük e színekkel az összes pontot. A színezés szabálya, hogy bármely két, egymást követő Pi , Pi+1(i = 1, 2, ... , n-1) pontra teljesüljön, hogy azonos színűek, vagy legalább az egyikük fehér. Hány szabályos színezés lehetséges?
|
|
|
| [2892] Csimby | 2009-03-30 20:30:37 |
 y=x-x3 és x=y3-y ugyanaz az origón átmenő görbe, csak 90 fokkal elforgatva. A tengelyeket (-1,0);(0,0);(1,0) illetve (0,1);(0,0);(0,-1) pontokban metszik. Más metszéspontjuk pedig nem lesz mint a (0,0) ez abból látszik, hogy a (-1,1)×(-1,1) négyzeten kívül mindegyik síknegyedben csak az egyik görbe halad. A négyzeten belül is a (-1,0)×(0,1); (0,1)×(0,1);(-1,0)×(0,-0);(0,1)×(0,-1) négyzetek mindegyikében csak az egyik görbe halad.
|
| Előzmény: [2891] Csimby, 2009-03-30 20:06:14 |
|
| [2891] Csimby | 2009-03-30 20:06:14 |
 Az egyik egyenletből kifejezzük y-t, majd a másikba helyettesítjük, így ezt kéne megoldani: x(2-2x2+3x4-3x6+x8)=0 A 0 lesz az egyik gyök nyilván. x2=z helyettesítéssel, keressük: 2-2z+3z2-3z3+z4=0 gyökeit. Ezek: 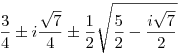 Tehát nem lesz több valós gyök. Biztos be lehet látni szebben is. Tehát nem lesz több valós gyök. Biztos be lehet látni szebben is.
|
| Előzmény: [2890] MTM, 2009-03-30 15:45:10 |
|
|
| [2889] Lóczi Lajos | 2009-03-30 03:05:09 |
 Adjuk meg az összes olyan x és y valós számot, melyekre fennáll, hogy x-x3-y=x+y-y3=0.
|
|
|
| [2886] Gábor1905 | 2009-03-12 10:26:30 |
 Üdv. A következő kérdésre szeretnék választ kapni:Van-e olyan konvex 5, vagy attól többszög, melynek 4-nél több belső szöge 120°, vagy annál kisebb. Minden ötlet nagyon érdekel! Előre is köszönöm!
|
|
| [2885] kutasp | 2009-03-11 20:22:39 |
 grat szép megoldás:) Amúgy fölmerül számos egyéb kérdés is a feladat kapcsán. 1., a te megoldásod és az általam ismert nagyon hasonló megoláds is burkoltan használja a kiválasztási axiómát, ugye akkor amikor választjuk a Hamel-bázist(ennek a létezését a vele ekvivalens Zorn-lemma biztosítja). Létezik-e ezt nem használó bizonyítás vagy esetleg ez állítás is ekvivalens a kiválasztási axiómával?
2., egyéb struktúrákra megnézni, hogy mikor színezhetők ki két színnel, konkrétabban:
a., Milyen véges Abel-csoportok színezhetők ki két színnel úgy, hogy mindkét színosztály zárt legyen a különböző elemekkel való csoportműveletre(azaz hatványozásra nem feltétlenül!)(erre úgy gondolom hogy tudom a választ)
b., ugyanez végtelen Abel-csoportokra
c., ugyanez tetszőleges csoportra
d., és az igazi általánosítás: ugyanez félcsoportokra, bár sztem ezek karakterizációja reménytelen, de esetleg érdemes megvizsgálni az ilyen félcsoportokat. Mindezt csak mint matematikus hallgató írom, tehát lehet hogy ennek az egész dolognak minden része ismert, ebben az esetben előre is elnézését kérem mindenkinek.
|
| Előzmény: [2881] jenei.attila, 2009-03-11 12:03:31 |
|
|
| [2883] Tibixe | 2009-03-11 18:09:52 |
 Ha jól látom, a lenti megoldás általánosítható 2c sok színre, mert egy színt meghatároz az, hogy melyik együtthatót követeljük nemnegatívnak és melyiket negatívnak. És kontinuum sok együttható van.
Színek egyesítésével pedig megkaphatunk bármilyen ennél kisebb számosságot.
Jól látom?
|
|
|
| [2881] jenei.attila | 2009-03-11 12:03:31 |
 Válaszolnék az alábbi valóban érdekes feladatra:
"Ki lehet-e színezni a pozitív valós számokat pirosra és kékre(mindkét színt kell használni), hogy pirosak összege piros, kékek összege kék legyen?"
Sokat agyaltam rajta, és úgy tűnik van ilyen színezés. A "valaki mondja meg" topikban feltettem néhány valós számokra vonatkozó algebrai kérdést, azokat is ez a feladat hozta elő. Tekintsük a valós számok testét a racionális számok teste feletti vektortérnek. Ennek a vektortérnek a bázisát Hamel bázisnak nevezik. Vagyis igaz az, hogy létezik a valós számok halmazának olyan H részhalmaza (ez a Hamel bázis), amellyel minden valós szám egyértelműen áll elő
r1h1+...+rnhn
alakban, ahol az r együtthatók racionális számok, a h számok pedig H elemei és n véges de függ az előállítandó számtól. Feltehetjük, hogy H tartalmazza az 1-et, és r1 az 1 együtthatója. Minden így előállított valós számot színezzünk pirosra, ha a h1 együttható (a szám "racionális része") nem negatív, kékre, ha r1 negatív. Így nyilván a valós számoknak egy jó színezését adjuk meg, és lesz kék pozitív szám is (pl.  , ha a , ha a 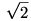 is eleme H-nak). is eleme H-nak).
|
| Előzmény: [2804] kutasp, 2009-01-07 22:02:55 |
|
| [2880] sakkmath | 2009-03-07 17:03:18 |
 Igazoljuk, hogy ha 1 < a < b < c, akkor
loga(logab) + logb(logbc) + logc(logca) > 0.
|
|
|
|






 3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét).
3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét). 



 esetén [C : K] is véges volna, ami az Artin-Schreier tétel szerint csak a K=R esetben lehet. Másrészt, ha A
esetén [C : K] is véges volna, ami az Artin-Schreier tétel szerint csak a K=R esetben lehet. Másrészt, ha A R egy maximális (nyilván
R egy maximális (nyilván 
 intervallumon
intervallumon
 z2 melyeknek az abszolut értéke is különbözik? Amugy itt van még egy kérdés: Bizonyitsuk be, hogy létezik
z2 melyeknek az abszolut értéke is különbözik? Amugy itt van még egy kérdés: Bizonyitsuk be, hogy létezik  >0 úgy hogy, ha
>0 úgy hogy, ha