| [3184] Fálesz Mihály | 2010-02-01 12:04:48 |
 Úgy látom, kezdenek forrósodni a kedélyek...
Szóval,
(p-1)!=(p-n)!.(p-n+1)(p-n+2)...(p-1) (p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p), (p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p),
és persze egyszerűsíthetünk bármivel, ami nem osztható p-vel.
De hol van ebben a Wilson-tétel?
|
|
|
| [3182] Róbert Gida | 2010-02-01 11:43:16 |
 Halál ismert példa, k=n-1 jelöléssel és osztással azt állítja a feladat, hogy 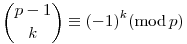 . Ami például Graham Konkrét matematika című könyvében az 5. fejezet 5. példája. És szerinte ez k=0-ra spec. esete a Wilson tételnek. Egy túróst. . Ami például Graham Konkrét matematika című könyvében az 5. fejezet 5. példája. És szerinte ez k=0-ra spec. esete a Wilson tételnek. Egy túróst.
|
| Előzmény: [3179] Maga Péter, 2010-02-01 08:11:25 |
|
| [3181] bily71 | 2010-02-01 09:43:04 |
 Saját! Ez az első "igazán komoly tételem", amit bizonyítanom is sikerült.:)
Ezzel a képlettel felgyorsítható a Wilson-teszt, hisz nem kell p-2 darab szorzást elvégezni, de még így is lassúbb, mint a naív módszer.
|
| Előzmény: [3179] Maga Péter, 2010-02-01 08:11:25 |
|
|
|
|
|
| [3176] Lóczi Lajos | 2010-01-30 17:50:28 |
 Valamely m nemnegatív valós szám esetén jelölje Hm azt a végtelen háromszögtartományt a nyílt jobboldali komplex félsíkon, amelynek z=a+bi (a>0) pontjaira fennáll, hogy |b| ma. ma.
Van-e olyan komplex függvény, amelyik értelmezve van a nyílt jobboldali komplex félsíkon (azaz a>0 esetén), ott (komplex értelemben) deriválható, és
- nem létezik a limesze az origóban, ha z 0 és a>0 (vagyis ha z a jobb félsíkból tetszőlegesen jőve közelíti meg a nullát) 0 és a>0 (vagyis ha z a jobb félsíkból tetszőlegesen jőve közelíti meg a nullát)
- viszont minden m 0 esetén létezik véges limesze az origóban, ha z 0 esetén létezik véges limesze az origóban, ha z 0 és z 0 és z Hm (vagyis ha z a háromszögtartományban haladva tart a nullához). (Igaz-e továbbá, hogy van olyan példa, hogy ez a létező véges limesz m-től függetlennek is választható?) Hm (vagyis ha z a háromszögtartományban haladva tart a nullához). (Igaz-e továbbá, hogy van olyan példa, hogy ez a létező véges limesz m-től függetlennek is választható?)
|
|
| [3175] bily71 | 2010-01-30 14:11:17 |
 Igaz-e, hogy ha p P, azaz prím, akkor P, azaz prím, akkor
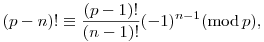
(n N és 0<n<p)? N és 0<n<p)?
|
|
| [3174] Horváth Bence | 2010-01-21 19:49:56 |
 Gézi ezt a feladatot nehéz meg csinálni de nagyon tetszik
|
|
|
| [3172] Radián | 2010-01-18 15:43:56 |
 Vegyük az egységsugarú kört és tegyük bele a négyzetünkbe(úgy hogy a négyzetünk és a kör középpontja egybeessen), majd forgassuk el úgy a körünket, hogy a kerületén kiválasztott A1 pont egybeessen a négyzet azon felezőpontjával (A2-vel), amely az R2 sugarú kör középpontja. Ha meghúzzuk az A1(=A2) pontból a megfelelő R1 sugarú kört akkor láthatjuk, hogy ez esetben négyzetünket nem osztottuk két egyenlő területű részre.(Hiszen R1<2 , így a kör a négyzetet két olyan pontban metszi melyek távolsága B ill C csúcstól (A2 eleme BC) kevesebb, mint 1/2. Így ha az R1 sugarú körrel (k1-gyel) eredeti körünket két egyenlő részre osztottuk, akkor négyzetünket a k1 kör nem fogja két egyenlő területű részre osztani.) Méghozzá az a rész lesz kisebb melyet tartalmaz a k1 kör. Így ahhoz hogy a négyzetünket két egyenlő területű részre oszthassuk egy R1-nél nagyobb sugarú R2 "körre" van szükségünk.
|
| Előzmény: [3171] Valezius, 2010-01-18 14:44:55 |
|
| [3171] Valezius | 2010-01-18 14:44:55 |
 Van egy egységsugarú kör, kijelölünk a kerületén egy pontot ahonnan R1 sugárral kört rajzolunk úgy, hogy a körív két azonos területű részre ossza a kört.
Van egy 2 egység oldalhosszúságú négyzetünk, az egyik oldal felezőpontjából R2 sugárral kört rajzolunk úgy, hogy a körív két azonos területű részre ossza a négyzetet.
Érzésre R1 vagy R2-e a nagyobb? Leginkább heurisztikus megoldás érdekelne, a konkrét értékek kiszámolása nélkül.
|
|
|
| [3169] Valezius | 2010-01-14 12:28:34 |
 Igen, bocsi. Az volt a baj, hogy a számlálóban a papíromon -1 szerepel, és nem +1. Tehát mégse ugyanaz jött ki, csak azt hittem.
|
|
| [3168] HoA | 2010-01-14 11:30:59 |
 Igen, a szögletes zárójel egészrészt jelöl . 10 golyóra a várható nyeremények k = 1,2,3,4,5 esetén nálam is 1 ; 1,8 ; 2,16 ; 2,016 ; 1,512 , tehát k=3 az optimum. 20 golyónál a gyök alatt négyzetszám van, valóban k = 4-re és 5-re egyformán 2,907 a várható nyeremény.
|
| Előzmény: [3164] Valezius, 2010-01-13 18:19:41 |
|
|
| [3166] jonas | 2010-01-13 21:07:05 |
 Szerintem ha 10 golyó van, akkor hármat kell húzni, mert akkor a várható nyeremény 2,16, míg ha csak kettőt húzunk, akkor 1,8. Még négyet is jobb húzni, mint kettőt.
|
| Előzmény: [3165] Valezius, 2010-01-13 18:33:36 |
|
|
| [3164] Valezius | 2010-01-13 18:19:41 |
 Idáig én is eljutottam, csak még nem találtam ki, hogy kéne kezelni, ha nem egészre jön ki. A zárójel az egész részt jelent nálad?
Mert 10-re, akkor ez 2,7-et ad, azaz 2-őt. De ott az elv alapján 3 golyónál kell megállni.
|
| Előzmény: [3163] HoA, 2010-01-13 17:17:06 |
|
|
| [3162] Sirpi | 2010-01-13 13:31:01 |
 1) igen, 1-től n-ig, mindegyik egyszer
2) igen, a k. külünbözzön az első k-1 mindegyikétől.
3) igen, k a nyeremény.
Szóval bár pongyola voltam, mindent jól gondoltál :-)
|
| Előzmény: [3161] HoA, 2010-01-13 12:40:06 |
|
| [3161] HoA | 2010-01-13 12:40:06 |
 - A golyók 1-től n-ig vannak számozva - minden szám egyszer szerepel?
- A "nem húztunk 2 egyformát" úgy értendő, hogy a k-iknak kihúzott golyó száma az addig kihúzott k-1 golyó egyikének számával sem egyezik?
- a nyeremény a kihúzott golyók DARABszáma, esetünkben k ?
|
| Előzmény: [3160] Sirpi, 2010-01-13 12:28:55 |
|
| [3160] Sirpi | 2010-01-13 12:28:55 |
 Akkor egy saját feladat:
Adott n számozott golyó, amik közül visszatevéssel húzunk. Bármikor megállhatunk, és ha nem húztunk 2 egyformát, akkor nyereményként a kihúzott golyók számát kapjuk, ha viszont igen, akkor így jártunk, nem kapunk semmit. A kérdés az, hogy adott n-re hány golyót kell kihúznunk, hogy maximalizáljuk a várható nyereményünket.
|
|



 (p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p),
(p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p),


 p feltétel.
p feltétel.

 0 és a>0 (vagyis ha z a jobb félsíkból tetszőlegesen jőve közelíti meg a nullát)
0 és a>0 (vagyis ha z a jobb félsíkból tetszőlegesen jőve közelíti meg a nullát)  0 esetén létezik véges limesze az origóban, ha z
0 esetén létezik véges limesze az origóban, ha z Hm (vagyis ha z a háromszögtartományban haladva tart a nullához). (Igaz-e továbbá, hogy van olyan példa, hogy ez a létező véges limesz m-től függetlennek is választható?)
Hm (vagyis ha z a háromszögtartományban haladva tart a nullához). (Igaz-e továbbá, hogy van olyan példa, hogy ez a létező véges limesz m-től függetlennek is választható?)
 esetén megy, tehát a [3147]-esben csak a=+
esetén megy, tehát a [3147]-esben csak a=+


