|
| [3386] Sirpi | 2010-12-07 13:20:04 |
 Nagyon jó a megfogalmazás :-)
Csak lehet, hogy valamit félreértek, mert túl könnyűnek tűnik ellenpéldát gyártani:
Legyen 3 város, A, B és C, és a kezdeti kétirányú (összefüggő) úthálózat álljon az AB és BC utakból (Mariska néni A-ban lakik, C-be akar eljutni). A kezdeti irányítás legyen C->B->A, ez Mariska néninek nyilván nem fog tetszeni. Erre CB-t megfordítják: C<-B->A, de ekkor B lesz forrás, így CB-t megint megfordítják: C->B->A s.í.t., Mariska néni pedig hoppon marad (persze ha másodszor nem CB-t, hanem BA-t fordítjuk meg, akkor meg is van a kívánt út, szóval meg lehet oldani, hogy eljusson, de azt is, hogy ne).
Ja, és ez nem csak 3 városra ellenpélda, mert nyilván ha B-be becsatlakozik még egy csomó másik út, mondjuk mind B-ből kifelé, akkor is ugyanezt el lehet mondani).
|
| Előzmény: [3385] Fálesz Mihály, 2010-12-07 12:48:40 |
|
| [3385] Fálesz Mihály | 2010-12-07 12:48:40 |
 516. feladat (Valamikor réges-régen, egy nem annyira távoli galaxisban, olimpiai előkészítőn volt.)
Bergengóciában olyan az úthálózat, hogy a városok közötti utak nem ágaznak el, minden út két várost köt össze. Az úthálózat összefüggő, vagyis az utakon bármelyik városból bármelyik városba el lehetett jutni --- legalábbis a múlt hétig. A világgazdasági válság miatt ugyanis a bergengóc kormány változatos megszorításokra kényszerült. Az Utazásról Leszoktató Minisztérium például a következőket rendelte el:
56789/2010. Min. rendelet a helyváltoztatás szabadságának megőrzéséről és védelméről
1.§ (a) Az ország mindegyik útját egyirányúsítani kell.
(b) Az utak irányítását olyan módon kell megválasztani, hogy ne lehessen körbe utazni több város között.
Az intézkedés bevezetése ellen hevesen tiltakoztak a kukutyiniak, mert hozzájuk minden út befelé vezetett, és emiatt sehova nem tudtak utazni. A demonstráció vezérszónoka Mariska néni volt, aki az unokahúga nagybátya sógorának a régi kollégiumi szobatárását szerette volna meglátogatni Alsómocsoládon. A tiltakozások eredményeként a minisztérium a következővel egészítette ki a rendeletet:
2.§ (a) Minden héten, ha van olyan város, ahonnan csak kifelé vezet út, akkor ezek közül ki kell választani az egyiket, és az innen kifelé vezető utak irányítását meg kell fordítani.
(b) Az (a) pont rendelkezéseiben előírtaktól eltekintve, a többi út irányítása nem változik.
Eljuthat-e Mariska néni Kukutyinból Alsómocsoládra?
|
|
| [3384] Tóbi | 2010-12-01 02:43:46 |
 Tényleg van explicit megoldás. Ha k lehetséges végkimenetel van, a idegen egymástól függetlenül a szelvényt vesz, mi pedig k darabot, akkor a nyereményünk várható összege 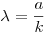 jelöléssel: jelöléssel:
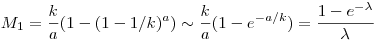
ha különböző szelvényeket veszünk,
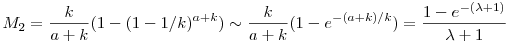
ha véletlenszerűen töltjük ki a szelvényeket.
|
| Előzmény: [3383] Róbert Gida, 2010-11-30 21:22:46 |
|
|
| [3382] Róbert Gida | 2010-11-30 21:20:15 |
 Itt szerintem neked feltételes valószínűséget kéne számolnod, ha összesen k darab telitalálat volt, akkor mennyi a valószínűsége, hogy ebből nekünk n darab telitalálatunk volt (persze 0 n n k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz. k). Amit te csinálsz a második szummában sehol nem jelenik meg k a valószínűségben, mást számolsz.
Az, hogy rossz, legkönnyebben úgy látod: b=k azaz, ha minden szelvény telitalálatos, ekkor persze csak az lehet, hogy az összes szelvényünk nyert, ami a te formuládból nem következik.
Egyszerűbb egyébként úgy számolni, hogy k1 darab telitalálat volt a 8 millió szelvényből, és k2 darab volt nekünk (dupla szumma lesz itt is). Tóbi megoldása mindenesetre szellemesebb és rövidebb.
|
| Előzmény: [3381] Füge, 2010-11-30 18:12:07 |
|
| [3381] Füge | 2010-11-30 18:12:07 |
 Tóbi, a második részben te csak azt az esetet nézed, mikor egy szelvénnyel nyerünk nem? A véletlen miatt többel is nyerhetünk egyszerre, ilyenkor meg nagyobb részét kapjuk meg a nyereménynek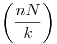 .Róbert Gida elmondanád kicsit részletesebben, hogy mi nem jó az én képletemben, mert nem igazán értem. Adott k érték esetén kiszámolom a nyereményem várható értékét, ezeket beszorzom a valószínűséggel, majd összegzem. Legalább is ezt akartam leírni. .Róbert Gida elmondanád kicsit részletesebben, hogy mi nem jó az én képletemben, mert nem igazán értem. Adott k érték esetén kiszámolom a nyereményem várható értékét, ezeket beszorzom a valószínűséggel, majd összegzem. Legalább is ezt akartam leírni.
|
|
|
| [3379] Tóbi | 2010-11-30 01:08:15 |
 Legyen 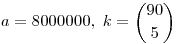 , a nyeremény 1. Az első esetet Füge már jól kiszámolta: , a nyeremény 1. Az első esetet Füge már jól kiszámolta:
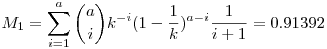
A 2. estben k szelvény van, mindegyik 1/k eséllyel nyer, így a nyeremény várható értéke egyenlő egy biztosan nyerő szelvény várható értékével. Ez az előzőek szerint számolható, csak a helyett a+k-1 további szelvény rontja az esélyeinket.
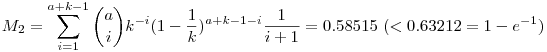
Az összegeket Maple-lel számoltam ki, i=100-ig.
|
| Előzmény: [3376] Róbert Gida, 2010-11-29 15:39:04 |
|
| [3378] Róbert Gida | 2010-11-29 22:43:33 |
 A második nem jó: b-ből kiválasztod a telitalálatosokat, aztán pedig a 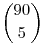 szelvényből a telitalálatosokat. szelvényből a telitalálatosokat.
Amúgy, ha csak közelítő eredmények érdeklik az embert, akkor elég elmenni addig, hogy legfeljebb mondjuk 100 telitalálat volt (már 100-nak is roppant kicsi az esély), továbbá nem racionális számokkal számolni, hanem lebegőpontossal, ha nem akarunk több millió jegyű számokkal szórakozni.
|
| Előzmény: [3377] Füge, 2010-11-29 20:23:06 |
|
| [3377] Füge | 2010-11-29 20:23:06 |
 Ha mindegyik szelvényt különbözően töltjük ki akkor biztosan 1 szelvénnyel fogunk nyerni, tehát a nyereményünk csak attól függ, hogy a többi szelvényből hány db nyert. Legyen a nyeremény: N, i db 5ös találat a 8.000.000 szelvényből és az egyszerűség kedvéért 8.000.000=a
![M_1=\sum_{i=0}^a\left[\binom{a}{i}\left[\frac{1}{\binom{90}{5}}\right]^i\left[1-\frac{1}{\binom{90}{5}}\right]^{(a-i)}\frac{N}{i+1}\right]](keplet.cgi?k=4E3895F80F12B0BC)
A második részt két változóval írtam fel, összesen k db telitalálat, ebből n db a miénk. 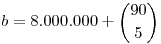
![M_2=\sum_{k=1}^b\left[\binom{b}{k}\left[\frac{1}{\binom{90}{5}}\right]^k\left[1-\frac{1}{\binom{90}{5}}\right]^{b-k}\sum_{n=0}^k\left[\binom{\binom{90}{5}}{n}\left[\frac{1}{\binom{90}{5}}\right]^n\left[1-\frac{1}{\binom{90}{5}}\right]^{\binom{90}{5}-n}\frac{nN}{k}\right]\right]](keplet.cgi?k=95E55BE97EE39516)
Gondolom, erre lehetne írni egy programot, ami szépen kiszámolja, de sajnos én nem tudok. Remélem, hogy jó, mert megszenvedtem a TeX-szel mire beírtam :)
|
|
| [3376] Róbert Gida | 2010-11-29 15:39:04 |
 A példa amúgy az idei Ankéton szerepelt: http://www.komal.hu/hirek/anket/2010/program2010.h.shtml Juhász István előadása.
Ez viszont már saját:
515. feladat Tegyük fel, hogy amikor már sokan játszanak a nagy nyereményért 8 millió szelvény érkezik be egy héten átlagosan. Mi történik, ha csak mi beszállunk és beküldünk 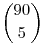 szelvényt. Mikor nagyobb a várható nyereményünk és mennyi (csak az ötös nyereményosztályban), ha véletlenszerűen töltjük ki a szelvényeket, vagy, ha mindegyiket különbözően? szelvényt. Mikor nagyobb a várható nyereményünk és mennyi (csak az ötös nyereményosztályban), ha véletlenszerűen töltjük ki a szelvényeket, vagy, ha mindegyiket különbözően?
(Csak egy hétig játszunk. Lottónál egy adott nyereményosztályban mindenki ugyanannyit kap.)
|
| Előzmény: [3371] Füge, 2010-11-28 19:55:48 |
|
|
|
|
|
|
| [3370] Róbert Gida | 2010-11-28 16:59:50 |
 514. feladat Véletlenszerűen kitöltünk 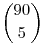 db ötöslottó szelvényt. Mennyi a valószínűsége, hogy lesz legalább egy öttalálatosunk? db ötöslottó szelvényt. Mennyi a valószínűsége, hogy lesz legalább egy öttalálatosunk?
|
|
| [3369] stray dog | 2010-11-26 16:18:14 |
 Köszönöm szépen!
Amúgy anno kihoztam hogy ha létezik vmelyik n-re ellenpélda, akkor minden m>n-re sem lehet igaz az állítás. Jelen esetben n=5, így minden 5-nél nagyobb értékre már nem teljesül az egyenlőtlenség.
|
| Előzmény: [3367] Tóbi, 2010-11-23 21:44:13 |
|
| [3368] jonas | 2010-11-23 22:19:07 |
 Ez a feladatcsokor a kedvencem, gonosz módon föladva. Ha így nehéz, kérhettek segítséget, mert tudok olyat mondani, ami még nem lő le mindent.
Legyen bármely n,k nemnegatív egészre ha n és k paritása azonos, akkor
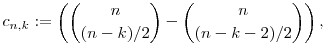
ha viszont n és k paritása különböző, akkor cn,k:=0. Épüljön fel a C négyzetes mátrix ezekből az elemekből, vagyis valamilyen N méretre legyen

Legyen H=CCT, azaz a H mátrix elemei
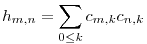
511. feladat Lássuk be, hogy a H visszafele csíkozott, azaz hm,n függvénye m-n-nek. Például h7,5=h8,4=h9,3=132.
512. feladat Mennyi H determinánsa?
Legyen bármely n,k nemnegatív egészre Un(x) az x-nek az az n-edfokú polinomja, amire Un(cos  )=sin ((n+1) )=sin ((n+1) )/sin )/sin  (ezeket másodfajú Csebisev-polinomnak hívják), és legyen un,k az xk együtthatója ebben a polinomban. Képezzük az un,k számokból is egy N méretű négyzetes U mátrixot. (ezeket másodfajú Csebisev-polinomnak hívják), és legyen un,k az xk együtthatója ebben a polinomban. Képezzük az un,k számokból is egy N méretű négyzetes U mátrixot.
513. feladat Számítsuk ki a CU szorzatot.
|
|
| [3367] Tóbi | 2010-11-23 21:44:13 |
 Ez pontosan az egyik kedvenc feladatom, pár éve magamtól vetettem fel, és hosszú agyalás után sikerült megoldani. Egy kis segítség a megoldáshoz:
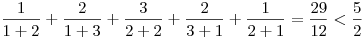
Próbálj ellenpéldát találni minden n 5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.) 5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.)
|
| Előzmény: [3365] stray dog, 2010-11-23 12:56:09 |
|
| [3366] D. Tamás | 2010-11-23 18:11:41 |
 n=3 esetén pont a Nesbitt-egyenlőtlenséget kapjuk, ami nevezetes. Egyébként a feladat igazolható a Titu-lemmával és a Számtani-mértani közepek közötti egyenlőtlenség felhasználásával.
|
| Előzmény: [3365] stray dog, 2010-11-23 12:56:09 |
|
| [3365] stray dog | 2010-11-23 12:56:09 |
 Sziasztok!
Igazából nem tudom hogy ebbe a topicba való-e, de ezt találtam a megfelelőbbnek. Szóval anno még középiskolásként a következő feladattal találkoztam:
Igaz-e, hogy ha x1,x2,...,xn tetsz. poz. valós számok, és n 3, akkor mindig fennáll a köv. egyenlőtlenség: 3, akkor mindig fennáll a köv. egyenlőtlenség:
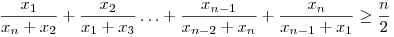
Az igazsághoz hozzátartozik még, hogy akkor nem tudtam megoldani. Most, hoszzú évek után, ismét kedvet kaptam egy kis matekozáshoz, de sajnos már nem rendelkezem a megfelelő ismerettel. Így a segítségeteket kérem. Az is jó, ha vki már látta a feladatot, és megadja, hogy hol érdemes utánanézni. Nekem úgy rémlik hogy a The American Mathematical Monthly-ban szerepelt még nagyon régen (60-as évek?), és akkor még mint megoldatlan probléma. Előre is köszönöm a segítséget! :)
|
|
|
|






 n
n

 )=sin ((n+1)
)=sin ((n+1) 5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.)
5-re és bizonyítani n=3,4-re. Végül határozd meg a kifejezés lehetséges legkisebb értékét (infimum). (Itt nem írok végeredményt, hadd gondolkodjon más is.)