| [3689] w | 2013-02-20 10:54:27 |
 Nem lövök le túl sokat, ha elmondom: az (a) részt a Róbert Gida által mondott módszerrel könnyebben meg lehet oldani, mint az eredetit, ujjgyakorlat. Átrendezve:
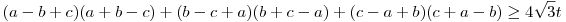 . .
Legyen x=-a+b+c, y=a-b+c, z=a+b-c, a Hérón-képlet miatt:
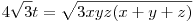 . Átírva az egyenlőtlenséget: . Átírva az egyenlőtlenséget:
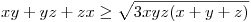
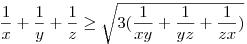
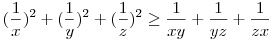 ismert, ekv. átalakítások miatt az eredeti is igaz. ismert, ekv. átalakítások miatt az eredeti is igaz.
|
| Előzmény: [3688] w, 2013-02-20 07:52:28 |
|
|
| [3687] Róbert Gida | 2013-02-19 21:46:12 |
 Nagyon ismerősnek tűnik. Gondolkodás nélkül: ha a,b,c egy háromszög oldalai, akkor a=y+z,b=x+z,c=x+y, ahol x=s-a,y=s-b,z=s-c és x,y,z>0 és ez visszafelé is igaz, ez nagyon hasznos az összes ilyen tipusú feladatnál, a háromszög kilőve. Héron képlettel: 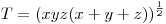 . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: . Ezt beírva és négyzetre emelve a két oldalt és rendezve a bizonyítandó: 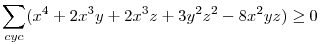 , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél. , ez pedig a számtani-mértani miatt igaz, az is látszik, hogy egyenlőség pontosan akkor van, ha x=y=z, azaz szabályos háromszögnél.
|
| Előzmény: [3686] w, 2013-02-19 19:37:40 |
|
| [3686] w | 2013-02-19 19:37:40 |
 Adott egy háromszög, oldalai: a, b, c; területe t. Igazoljuk:
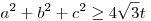 . .
|
|
| [3685] jenei.attila | 2013-02-19 12:10:49 |
 Megnéztem a megoldást, szerintem a két konstrukció hasonló elvű, csak az enyém egyszerűbb. Egyébként először én is ezt a "hivatalos" megoldást adtam meg, és azután egyszerűsítettem.
|
| Előzmény: [3684] m2mm, 2013-02-19 00:26:45 |
|
| [3684] m2mm | 2013-02-19 00:26:45 |
 1 megoldásra emlékszem, az a hivatalos, megtalálható a 3681 hozzászólás linkjében. És igen, RMM a mostani hiv. név, régen volt ez RMMS, nekünk RMMC(C for competition) néven volt ismert.
|
| Előzmény: [3683] jenei.attila, 2013-02-16 08:42:56 |
|
|
|
|
|
| [3679] jenei.attila | 2013-02-15 08:30:10 |
 Ezt nem tudtam, de aki ismeri vagy megoldotta, azzal megbeszélhetjük. Az én megoldásom:
f(x)=(-1)[x]xhax>0
f(0)=0
f(x)=-f(-x)hax<0
g(x)=(-1)[x](x+1)hax>0
g(0)=0
g(x)=-g(-x)hax<0
|
| Előzmény: [3678] m2mm, 2013-02-15 05:05:37 |
|
|
|
| [3676] jenei.attila | 2013-02-14 21:09:19 |
 Képlettel:
(1*9+2*8+3*7+4*6+5*5+6*4+7*3+8*2+9*1)*20/4
Ez a következőképpen jön ki: a pontokat számozzuk 1-től 20-ig a körvonalon egymás után. Az első kiválasztott pont legyen az 1-es. Ekkor a 3-adik kiválasztott pont (körbehaladva számozva)7-estől 15-ösig lehet. Ha a 7-es a 3.-adik kiválasztott pont, akkor a 2. kiválasztott csak a 4-es lehet, a 4.-edik kiválasztott pedig 10-estől 18-asig 9 féle lehet. Ha 8-as a 3. kiválasztott pont, akkor a 2. kiválasztott 4-es és 5-ös lehet, a 4. kiválasztott 11-18-ig mehet. És így tovább: az 1. kiválasztott pont rögzítése mellet
1*9+2*8+3*7+4*6+5*5+6*4+7*3+8*2+9*1
jó kiválasztás létezik. Az 1. kiválasztott pontot 20 féleképpen rögzíthetjük, vagyis a jó kiválasztásokat úgy számolhatjuk össze, hogy a most kapott értéket 20-szal szorozzuk, de akkor minden egyes kiválasztást 4-szer számolunk, hiszen bármelyik pontját tekinthetjük 1. kiválasztott pontnak.
|
| Előzmény: [3675] Róbert Gida, 2013-02-14 18:55:51 |
|
|
| [3674] jenei.attila | 2013-02-14 09:43:24 |
 Adott a körvonalon 20 pont. Hányféleképpen választható ki ezek közül 4 pont úgy, hogy bármely két kiválasztott pont között legalább két ki nem választott pont fekszik. Erre a feladatra válaszoltam, ha jól értettem az angol szöveget. Tehát a válasz 825. Legalábbis szerintem. Szerintetek?
|
| Előzmény: [3673] jenei.attila, 2013-02-11 11:04:24 |
|
|
|
| [3671] juantheron | 2013-02-08 06:41:53 |
 There are 20 points in a circle A1,A2,...A20.
Find the number of ways of selecting 4 points such that
there are at-least two points in between any two selected
points.
|
|
| [3670] w | 2013-02-05 16:59:02 |
 Nem sokan foglalkoztak a feladattal, elmondom a megoldást. Legyen  si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy
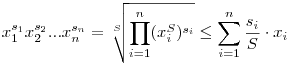 , ,
ahol a súlyozott mértani és számtani közép egyenlőtlenségét használtuk ki. Mindegyik tagot a jobb oldalon hasonlóan megbecsülve, majd az egyenlőtlenségeket összegezve a bizonyítandó adódik, hiszen az egyes xi számok előtt minden lehetséges 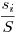 szorzótényező szerepel, és ezek összege 1. szorzótényező szerepel, és ezek összege 1.
|
| Előzmény: [3649] w, 2013-01-13 21:25:23 |
|
| [3669] jenei.attila | 2013-02-05 14:34:25 |
 Egy érdekes feladat: Léteznek-e f:R->R és g:R->R függvények úgy, hogy x->g(f(x)) szigorúan monoton növő, x->f(g(x)) pedig szigorúan monoton fogyó.
|
|
| [3668] marcius8 | 2013-02-04 15:48:49 |
 Tisztelt Látogatók!
Egy játékot találtam ki. Mivel egy játékkal akkor foglalkoznak sokan, ha szabályai egyszerűek, ugyanakkor nem könnyen végigjátszható, ezért a következő játékot találtam ki:
A magyar kártyacsomag összetétele: A magyar kártyacsomag 32 lapot tartalmaz. Minden lapnak van színe és értéke. A színek lehetnek: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél). Az értékek lehetnek: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”. A kártyacsomagban minden lehetséges szín-érték párosítás előfordul.
A nyolc sorból és négy oszlopból álló táblázatban elhelyezett magyar kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek:
• A táblázat minden oszlopában található négy lap színének sorrendje felülről lefelé haladva: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél).
• A táblázat minden sorában található nyolc lap értékének sorrendje balról jobbra haladva: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”.
A játék szabálya: A kártyacsomag lapjai véletlenszerű sorrendben egy négy sorból és nyolc oszlopból álló táblázatban vannak elhelyezve. A játék során egyszerre mindig két lapot lehet megcserélni. Két lapot csak akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá (és) ha a két lap színe vagy értéke ugyanaz. A játék célja, hogy a kártyalapok sorrendje rendezett legyen.
Az érdekes az hogy a véletlenszerűen összekevert állapotból majdnem mindig abba az állapotba jutok, hogy a rendezett állapothoz képest a "makk ász" és a "tök király" fel van cserélve. Sajnos, nem tudok rájönni, hogy ez az én ügyetlenségem (gyanítom, hogy igen), de ugyanakkor nem hiszem hogy ennek törvényszerűen így kell lenni. Arra kérek bárkit, hogy ha ezt a jelenséget meg tudja indokolni, vagy meg tudja oldani (tehát ha a rendezett állapothoz képest csak a "makk ász" és a "tök király" van felcserélve, akkor ez az állapot rendezhető vagy sem), írjon a marcius.08@freemail.hu címre.
|
|
|
| [3666] ibiro | 2013-02-02 21:00:07 |
 Sajnos nem értem melyik jobb oldalra gondolsz, a [3649]-ben ? És miért a negyedik hatványra ? Még nincs bizonyitva hogy a [3652] igaz n-re is !
|
| Előzmény: [3665] w, 2013-02-01 19:25:15 |
|
|






 si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy
si=S. Tekintsük a jobb oldalon szereplő pl. első tagot, ez olyan alakba is írható, hogy 
 a2bc+ab2c+abc2-ben
a2bc+ab2c+abc2-ben